PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 130: | Linia 130: | ||
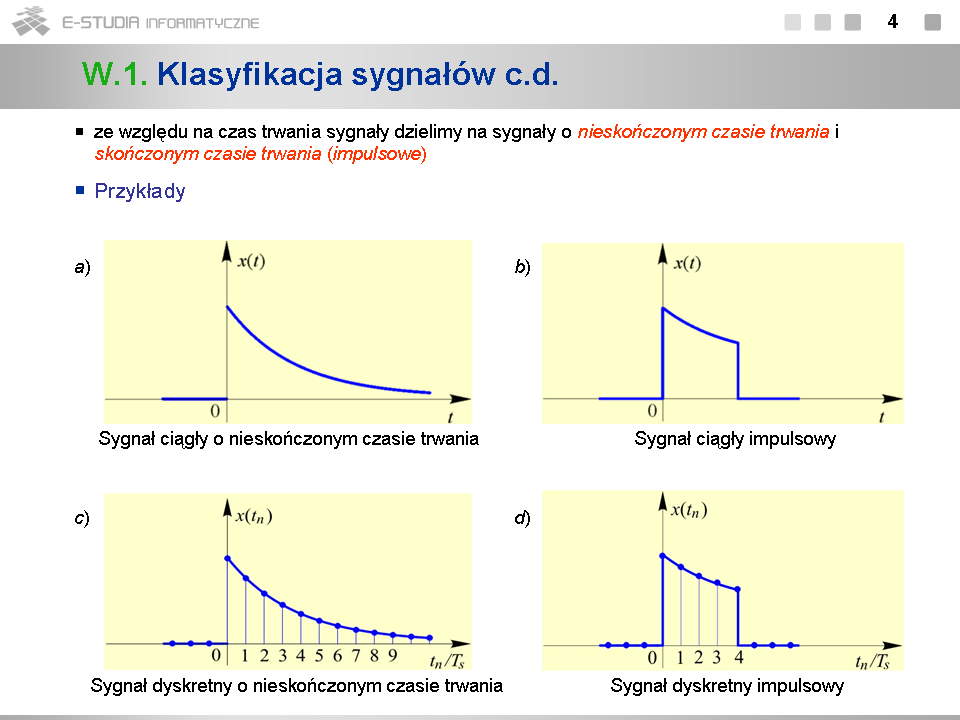
*Sygnał skoku jednostkowego pokazany na rys. b) jest oznaczany symbolem specjalnym <math>1(t)\,</math> , używanym również w teorii obwodów. Zapis <math>X_01(t-t_0)\,</math> oznacza skok o wartość <math>X_0\,</math> w chwili <math>t_0\,</math> . | *Sygnał skoku jednostkowego pokazany na rys. b) jest oznaczany symbolem specjalnym <math>1(t)\,</math> , używanym również w teorii obwodów. Zapis <math>X_01(t-t_0)\,</math> oznacza skok o wartość <math>X_0\,</math> w chwili <math>t_0\,</math> . | ||
*Sygnał wykładniczy narastający z rys. c) jest np. sygnałem napięcia na kondensatorze ładowanym przez opór z idealnego źródła napięciowego. | *Sygnał wykładniczy narastający z rys. c) jest np. sygnałem napięcia na kondensatorze ładowanym przez opór z idealnego źródła napięciowego. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd11.png]] | |||
|valign="top"| | |||
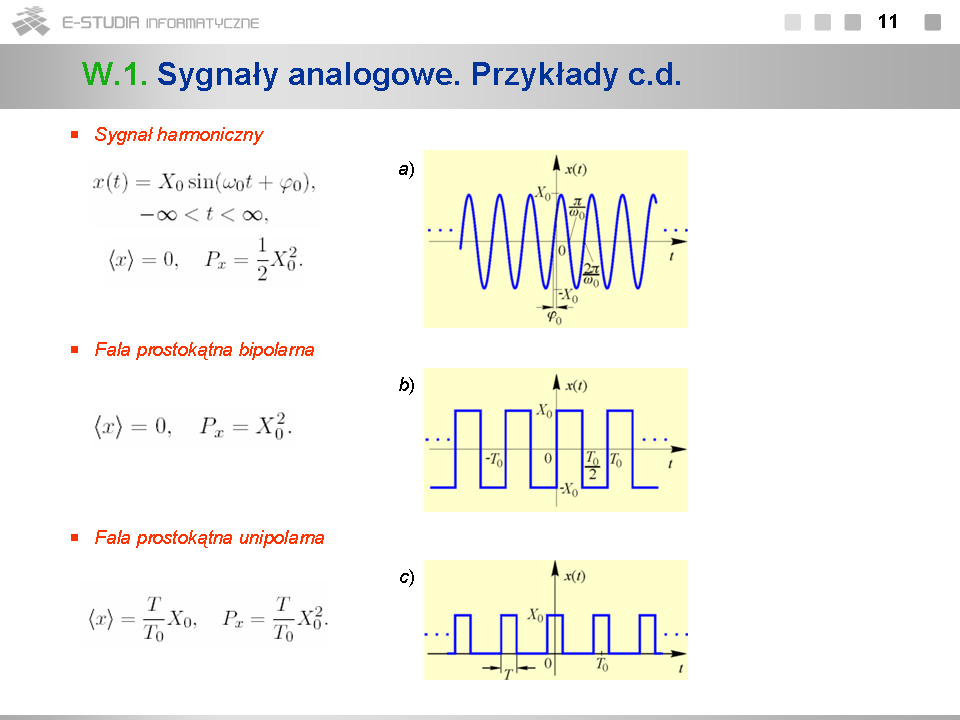
*Na rys. a), b) i c) są pokazane przykłady najczęściej spotykanych sygnałów okresowych. Są to oczywiście sygnały o ograniczonej mocy. Pełnią one w praktyce rolę sygnałów nośnych w różnych systemach modulacji sygnałów, a także sygnałów synchronizujących. | |||
*Sygnał harmoniczny (rys. a) jest określony przez trzy parametry: amplitudę <math>X_0\,</math> , pulsację <math>\omega_0\,</math> (lub częstotliwość <math>f_0=\omega_0/2\pi=1/T_0</math> , gdzie <math>T_0\,</math> jest okresem), oraz fazę początkową <math>\varphi_0\,</math> . Jest on wykorzystywany m.in. jako fala nośna w ''analogowych systemach modulacji''. | |||
*Fala prostokątna bipolarna (rys. b) jest wykorzystywana jako przebieg synchronizujący i zegarowy, zaś fala prostokątna unipolarna (rys. c) jako przebieg nośny w ''impulsowych systemach modulacji''. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd12.png]] | |||
|valign="top"| | |||
*Funkcje <math>|z(t)|=\sqrt{x^2(t)+y^2(t)}</math> i <math>arg\, z(t)=arctg[y(t)/x(t)]</math> noszą nazwę ''modułu'' i odpowiednio ''argumentu'' sygnału <math>z(t)\,</math> . Są to funkcje rzeczywiste czasu. | |||
*Sygnały zespolone również dzielimy na sygnały o ograniczonej energii i sygnały o ograniczonej mocy. W przypadku sygnałów zespolonych we wzorach definiujących energię (1.6) i moc (1.7) lub (1.8) należy w wyrażeniu podcałkowym uwzględnić nie kwadrat sygnału <math>x^2(t)\,</math> , a kwadrat modułu sygnału <math>|x^2(t)|\,</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd13.png]] | |||
|valign="top"| | |||
*''Sygnał harmoniczny zespolony'' <math>z(t)=e^{j\omega_0 t}</math> (1.11), nazywany także sinusoidą zespoloną, jest często wykorzystywany do reprezentacji rzeczywistego sygnału harmonicznego <math>x(t)=cos\omega_0 t</math> , przy czym <math>x(t)=Re\, z(t)</math> . Jest to oczywiście sygnał o ograniczonej mocy. Jego moc, jak można łatwo sprawdzić korzystając ze zmodyfikowanego wzoru (1.8), jest równa 1. | |||
*Sygnałami harmonicznymi zespolonymi posługujemy się również w innych reprezentacjach sygnałów rzeczywistych, np. zbiór sygnałów tworzy tzw. bazę rozwinięcia sygnału okresowego o okresie w zespolony szereg Fouriera (por. wzór (1.2)). | |||