PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd1.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd1.png]] | ||
|valign="top"| | |valign="top"| | ||
*Za pomocą sygnałów przekazywana jest informacja. Często mówi się, że sygnał jest ''nośnikiem informacji''. | *Za pomocą sygnałów przekazywana jest informacja. Często mówi się, że sygnał jest ''nośnikiem informacji''. | ||
| Linia 13: | Linia 13: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd2.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd2.png]] | ||
|valign="top"| | |valign="top"| | ||
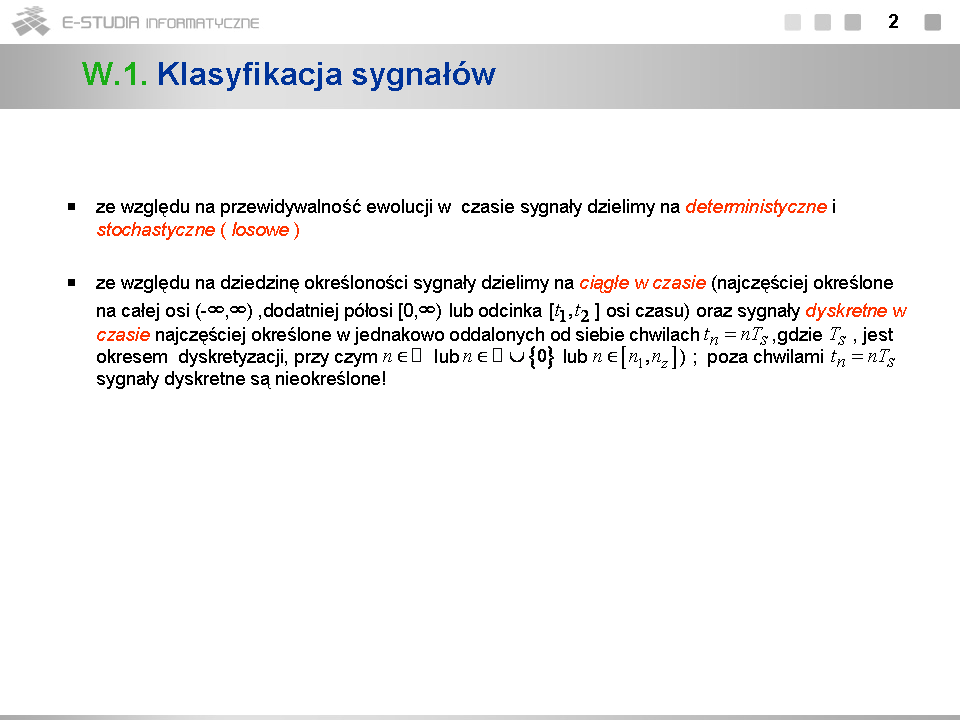
*Rozważania ograniczymy wyłącznie do ''sygnałów determi¬nistycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | *Rozważania ograniczymy wyłącznie do ''sygnałów determi¬nistycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | ||
| Linia 30: | Linia 30: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd3.png]] | ||
|valign="top"| | |valign="top"| | ||
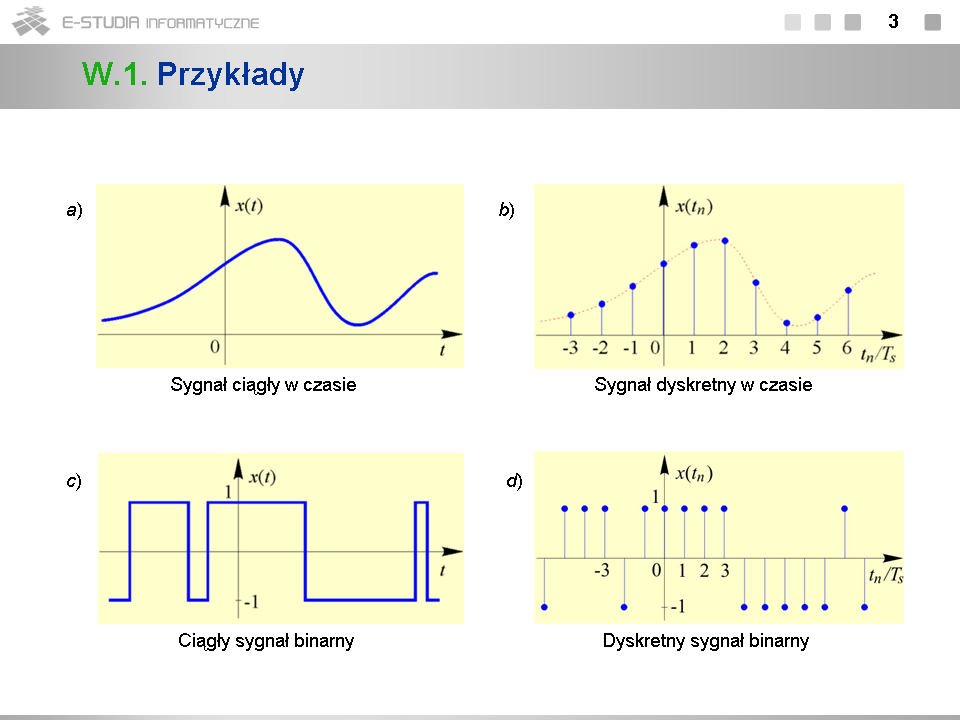
*Zwróćmy uwagę, że sygnały przedstawione na rys. b) i d) otrzymujemy w wyniku próbkowania sygnałów z rys. a) i odpowiednio c). Z sygnałami powstałymi w wyniku próbkowania sygnałów analogowych mamy w praktyce do czynienia najczęściej. Sygnałami dyskretnymi mogą być jednak także sygnały nie mające pierwowzorów analogowych, np. ciąg notowań dziennych kursu złotówki do dolara. Podkreślmy, że sygnał dyskretny jest w istocie rzeczy ciągiem liczb. | *Zwróćmy uwagę, że sygnały przedstawione na rys. b) i d) otrzymujemy w wyniku próbkowania sygnałów z rys. a) i odpowiednio c). Z sygnałami powstałymi w wyniku próbkowania sygnałów analogowych mamy w praktyce do czynienia najczęściej. Sygnałami dyskretnymi mogą być jednak także sygnały nie mające pierwowzorów analogowych, np. ciąg notowań dziennych kursu złotówki do dolara. Podkreślmy, że sygnał dyskretny jest w istocie rzeczy ciągiem liczb. | ||
| Linia 41: | Linia 41: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
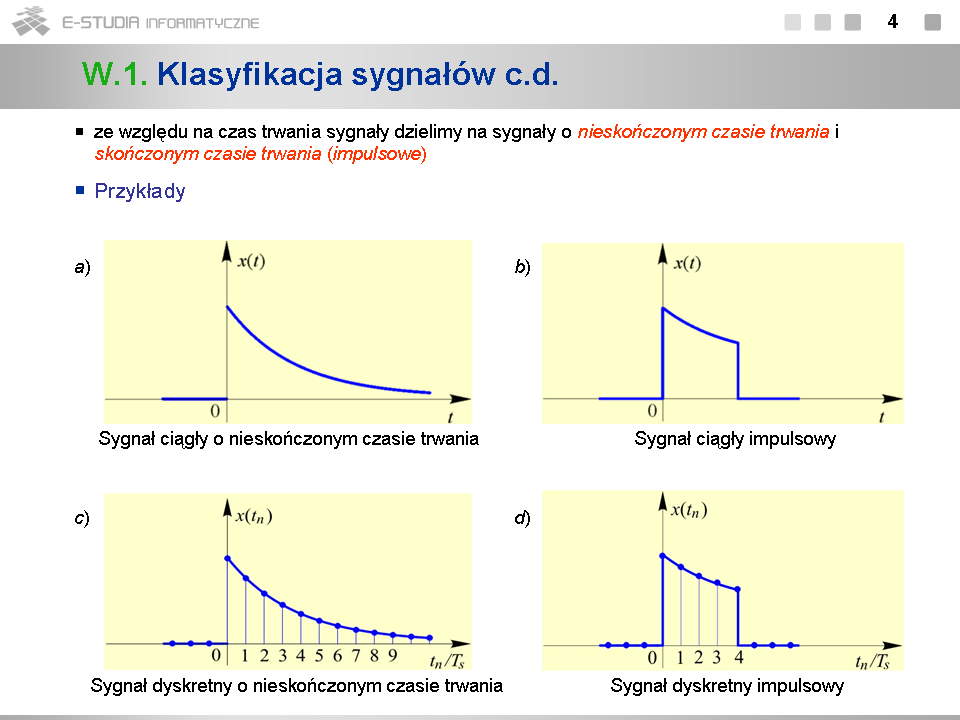
*Podobnie jak w poprzednich przykładach, sygnały z rys. c) i d) są spróbkowanymi sygnałami z rys. a) i b). | *Podobnie jak w poprzednich przykładach, sygnały z rys. c) i d) są spróbkowanymi sygnałami z rys. a) i b). | ||
| Linia 52: | Linia 52: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd5.png]] | ||
|valign="top"| | |valign="top"| | ||
* Reprezentację sygnału harmonicznego stanowi liczba zespolona <math>Ae^{j\varphi}\,</math> , nazywana ''amplitudą zespoloną'', gdzie <math>A\,</math> jest amplitudą sygnału, a <math>\varphi\,</math> – jego fazą. | * Reprezentację sygnału harmonicznego stanowi liczba zespolona <math>Ae^{j\varphi}\,</math> , nazywana ''amplitudą zespoloną'', gdzie <math>A\,</math> jest amplitudą sygnału, a <math>\varphi\,</math> – jego fazą. | ||
| Linia 71: | Linia 71: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
*Parametry sygnałów są ich globalnymi charakterystykami liczbowymi. Definicje poszczególnych parametrów są zróżnicowane w zależności od klasy sygnału. | *Parametry sygnałów są ich globalnymi charakterystykami liczbowymi. Definicje poszczególnych parametrów są zróżnicowane w zależności od klasy sygnału. | ||
| Linia 82: | Linia 82: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd7.png]] | ||
|valign="top"| | |valign="top"| | ||
*''Energia, moc średnia'' (krótko moc) i ''wartość skuteczna'', należą do najważniejszych parametrów sygnału. Wielkości te są nazywane ''parametrami energetycznymi'' sygnałów. Ponieważ założyliśmy, że sygnały są wielkościami bezwymia¬rowymi, ich energię określoną wzorem (1.6) wyrażamy w sekundach, moc zaś określona wzorami (1.7) lub (1.8) oraz wartość skuteczna są bezwymiarowe. | *''Energia, moc średnia'' (krótko moc) i ''wartość skuteczna'', należą do najważniejszych parametrów sygnału. Wielkości te są nazywane ''parametrami energetycznymi'' sygnałów. Ponieważ założyliśmy, że sygnały są wielkościami bezwymia¬rowymi, ich energię określoną wzorem (1.6) wyrażamy w sekundach, moc zaś określona wzorami (1.7) lub (1.8) oraz wartość skuteczna są bezwymiarowe. | ||
| Linia 101: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika:PS_M1_Slajd8.png]] | |width="500px" valign="top"|[[Grafika:PS_M1_Slajd8.png]] | ||
|valign="top"| | |valign="top"| | ||
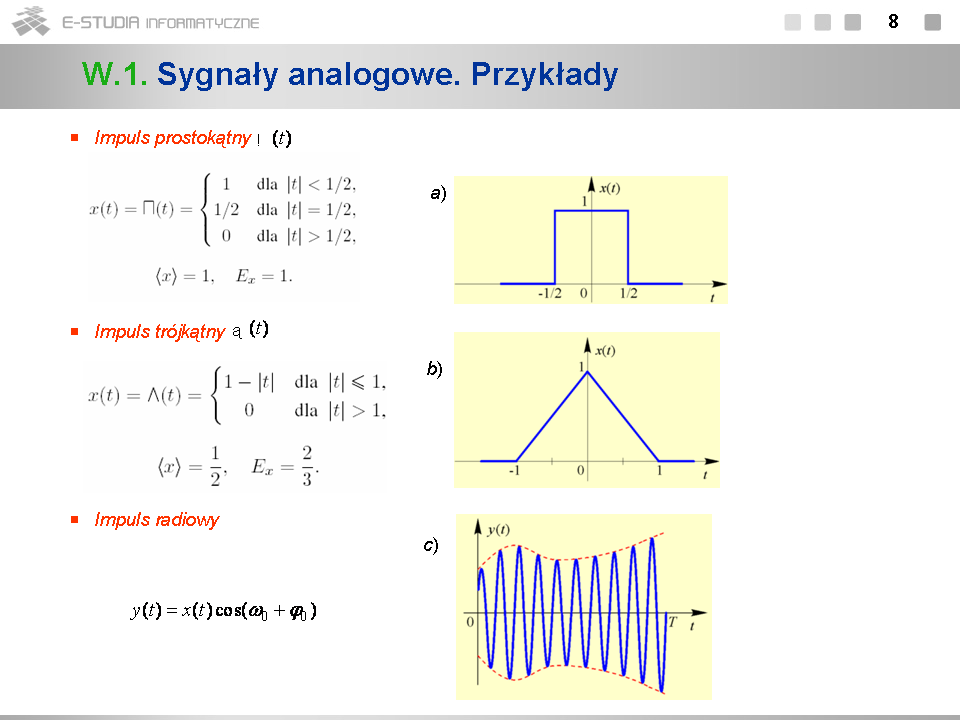
*Sygnał pokazany na rys. a) jest symetrycznym unormowanym impulsem prostokątnym o jednostkowym czasie trwania i jednostkowej amplitudzie. Jego wartość średnia i energia są również równe jedności. Został on oznaczony specjalnym symbolem <math>\Pi(t)\,</math> . Posługując się tym symbolem, możemy zapisać dowolny impuls prostokątny o wysokości <math>a\,</math> , szerokości <math>b\,</math> i przesunięty względem zera o czas <math>c\,</math> w postaci <math>a\Pi[(t-c)/b]\,</math> .Również inne standardowe sygnały będą oznaczane wygodnymi w użyciu symbolami specjalnym, np. symetryczny impuls trójkątny <math>\Lambda(t)\,</math> z rys. b. Podkreślmy, że w przeciwieństwie do impulsu prostokątnego <math>\Pi(t)\,</math> czas trwania impulsu trójkątnego <math>\Lambda(t)\,</math> jest z definicji równy 2. | *Sygnał pokazany na rys. a) jest symetrycznym unormowanym impulsem prostokątnym o jednostkowym czasie trwania i jednostkowej amplitudzie. Jego wartość średnia i energia są również równe jedności. Został on oznaczony specjalnym symbolem <math>\Pi(t)\,</math> . Posługując się tym symbolem, możemy zapisać dowolny impuls prostokątny o wysokości <math>a\,</math> , szerokości <math>b\,</math> i przesunięty względem zera o czas <math>c\,</math> w postaci <math>a\Pi[(t-c)/b]\,</math> .Również inne standardowe sygnały będą oznaczane wygodnymi w użyciu symbolami specjalnym, np. symetryczny impuls trójkątny <math>\Lambda(t)\,</math> z rys. b. Podkreślmy, że w przeciwieństwie do impulsu prostokątnego <math>\Pi(t)\,</math> czas trwania impulsu trójkątnego <math>\Lambda(t)\,</math> jest z definicji równy 2. | ||
*Impulsy radiowe (rys. c), spotyka się zwykle w radiokomunikacji, telekomunikacji oraz technice radarowej i sonarowej. Sygnał <math>x(t)\,</math> jest dowolnym sygnałem impulsowym (często prostokątnym) i jest nazywany ''obwiednią'' sygnału <math>y(t)\,</math> , a sygnał <math>cos(\omega_0 t+\varphi_0)\,</math> – jego ''wypełnieniem''. Z reguły, czego siłą rzeczy nie oddaje rysunek, okres wypełnienia <math>T_0=2\pi/{\omega_0} </math> jest dużo mniejszy od czasu trwania impulsu <math>y(t)\,</math> . | *Impulsy radiowe (rys. c), spotyka się zwykle w radiokomunikacji, telekomunikacji oraz technice radarowej i sonarowej. Sygnał <math>x(t)\,</math> jest dowolnym sygnałem impulsowym (często prostokątnym) i jest nazywany ''obwiednią'' sygnału <math>y(t)\,</math> , a sygnał <math>cos(\omega_0 t+\varphi_0)\,</math> – jego ''wypełnieniem''. Z reguły, czego siłą rzeczy nie oddaje rysunek, okres wypełnienia <math>T_0=2\pi/{\omega_0} </math> jest dużo mniejszy od czasu trwania impulsu <math>y(t)\,</math> . | ||