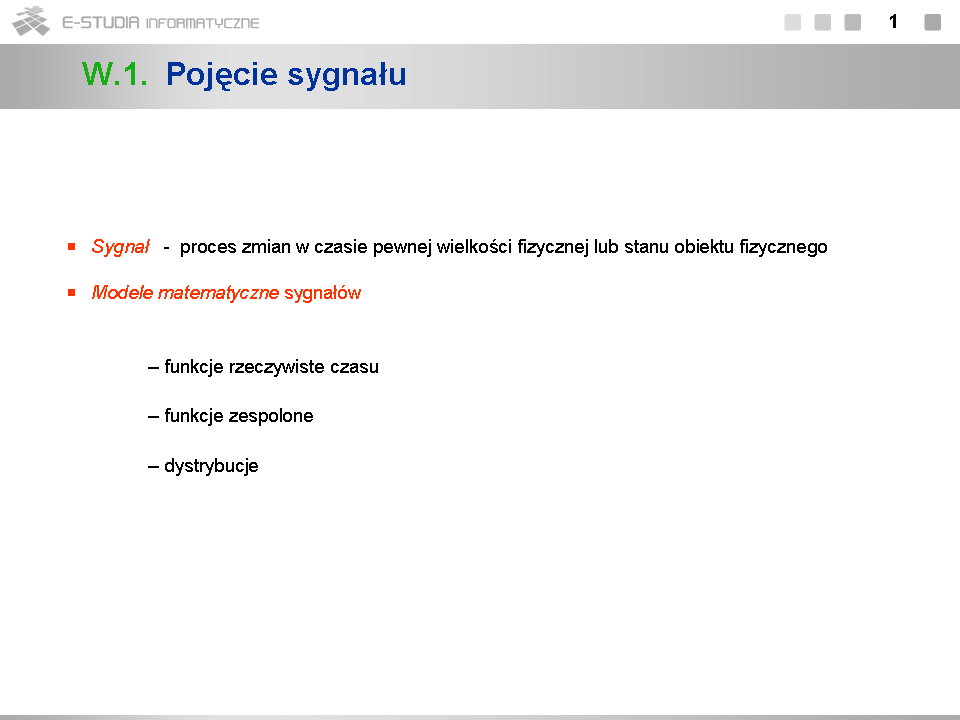
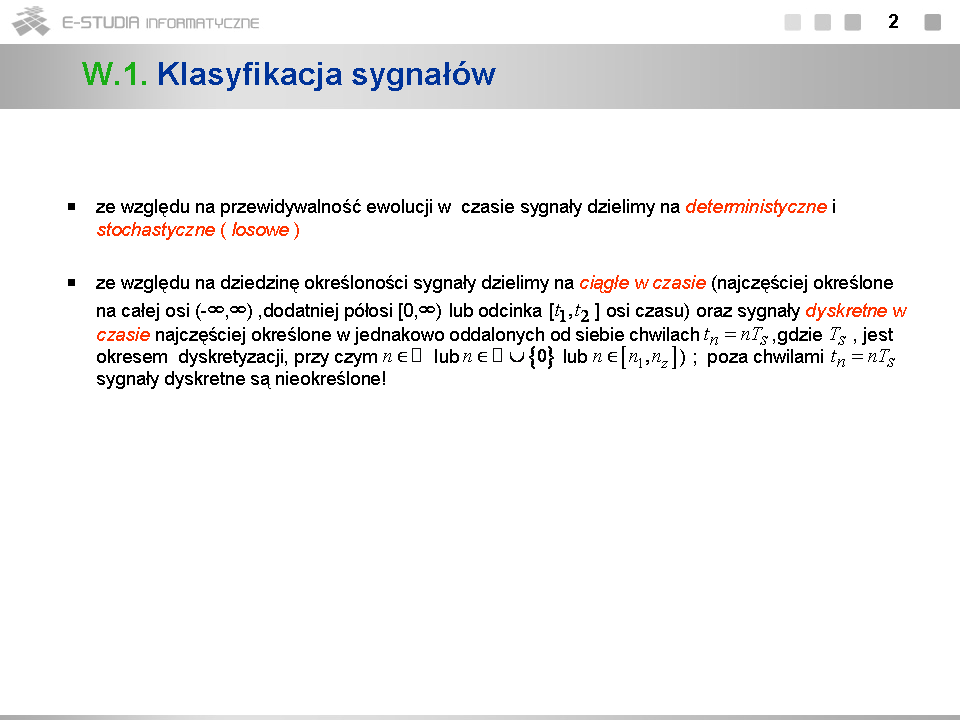
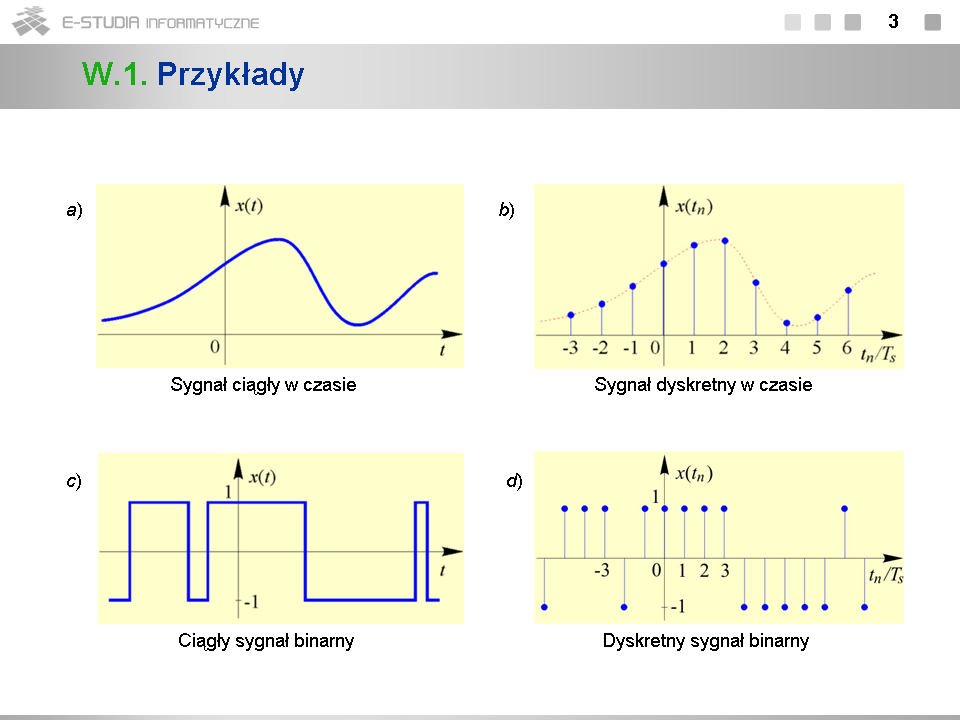
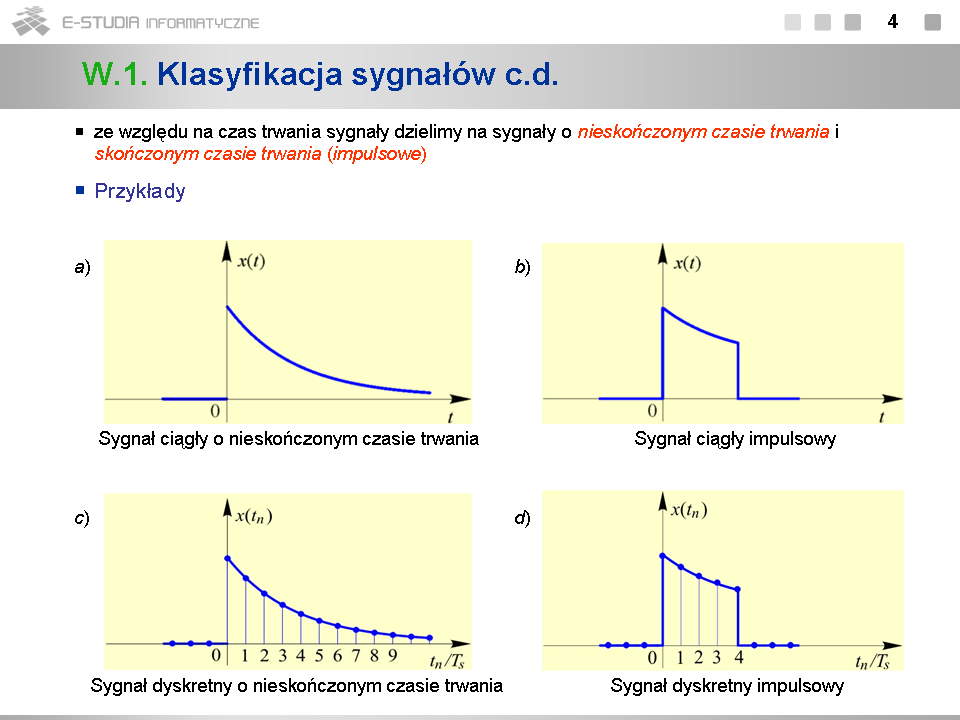
PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 56: | Linia 56: | ||
* Reprezentację sygnału harmonicznego stanowi liczba zespolona <math>Ae^{j\varphi}\,</math> , nazywana ''amplitudą zespoloną'', gdzie <math>A\,</math> jest amplitudą sygnału, a <math>\varphi\,</math> – jego fazą. | * Reprezentację sygnału harmonicznego stanowi liczba zespolona <math>Ae^{j\varphi}\,</math> , nazywana ''amplitudą zespoloną'', gdzie <math>A\,</math> jest amplitudą sygnału, a <math>\varphi\,</math> – jego fazą. | ||
*W przypadku rozwinięcia sygnału okresowego o ustalonym okresie <math>T_0\,</math> w rzeczywisty trygonometryczny szereg Fouriera (1.1) jego reprezentacja jest zbiór liczb rzeczywistych <math>\left \{a_0, a_k, b_k : k\epsilon\Box \right \} \,</math> (zbiór ''współczynników Fouriera''), zaś w przypadku rozwinięcia w zespolony trygonometryczny szereg Fouriera (1.2) – zbiór liczb zespolonych <math>X_k : k\epsilon\Box\,</math> . | *W przypadku rozwinięcia sygnału okresowego o ustalonym okresie <math>T_0\,</math> w rzeczywisty trygonometryczny szereg Fouriera (1.1) jego reprezentacja jest zbiór liczb rzeczywistych <math>\left \{a_0, a_k, b_k : k\epsilon\Box \right \} \,</math> (zbiór ''współczynników Fouriera''), zaś w przypadku rozwinięcia w zespolony trygonometryczny szereg Fouriera (1.2) – zbiór liczb zespolonych <math>\left \{X_k : k\epsilon\Box\right \}\,</math> . | ||