PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 13: | Linia 13: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px"|[[Grafika: | |width="500px"|[[Grafika:PS_M1_Slajd2.png]] | ||
|valign="top"| | |valign="top"| | ||
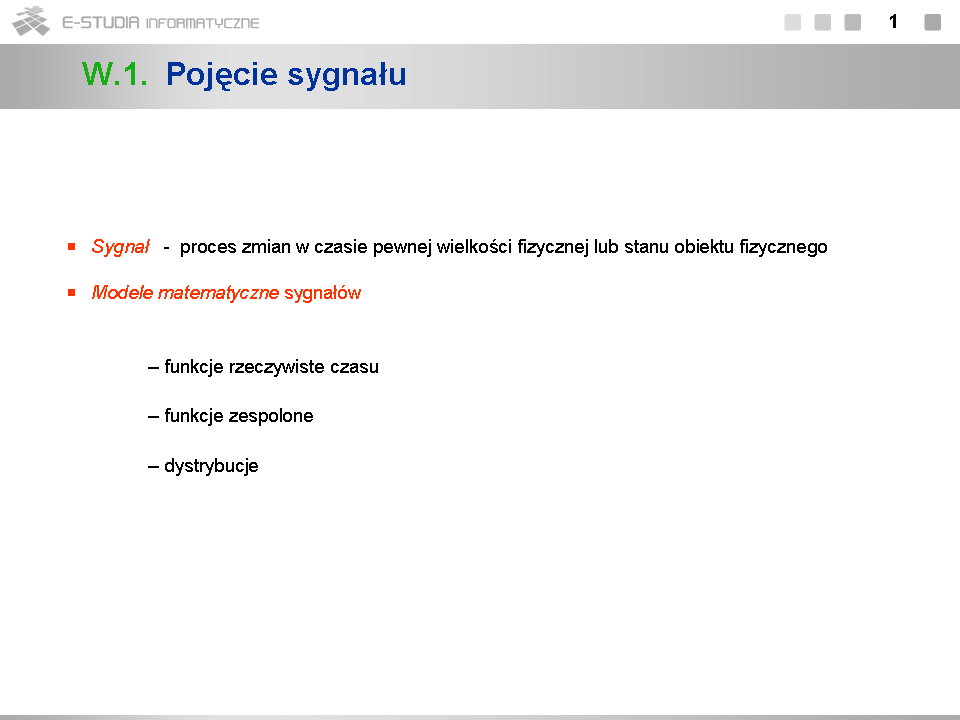
*Rozważania ograniczymy wyłącznie do ''sygnałów determi¬nistycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | *Rozważania ograniczymy wyłącznie do ''sygnałów determi¬nistycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | ||
| Linia 24: | Linia 24: | ||
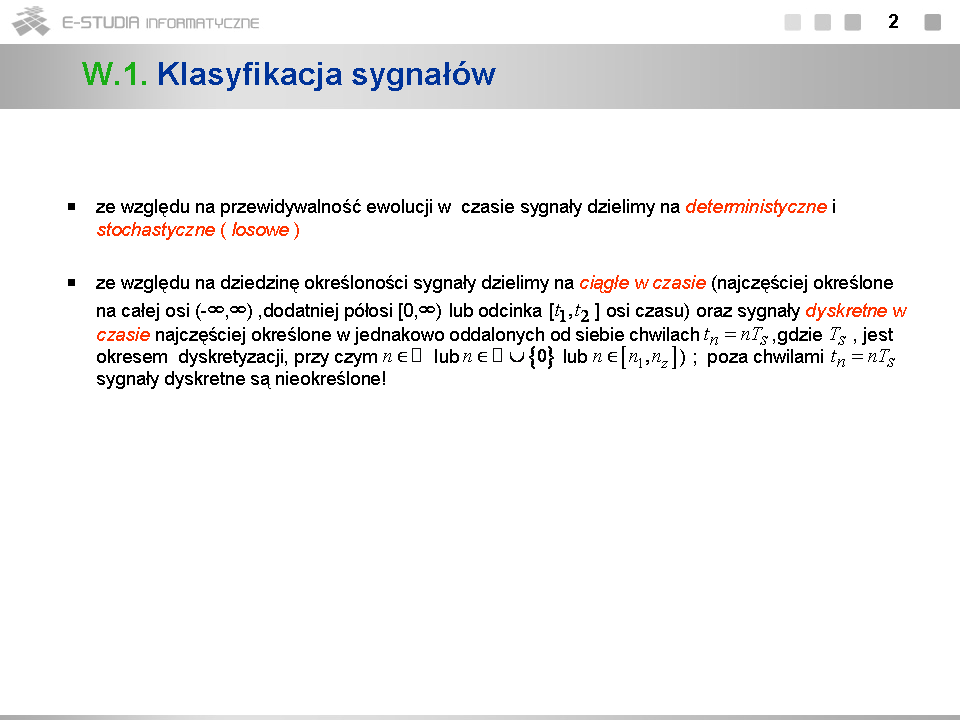
*W klasie sygnałów dyskretnych wyróżniamy sygnały ''binarne'', które przybierają w każdej chwili tylko dwie wartości binarne (np. 0 i 1 lub 1 i –1 ). | *W klasie sygnałów dyskretnych wyróżniamy sygnały ''binarne'', które przybierają w każdej chwili tylko dwie wartości binarne (np. 0 i 1 lub 1 i –1 ). | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px"|[[Grafika:PS_M1_Slajd3.png]] | |||
|valign="top"| | |||
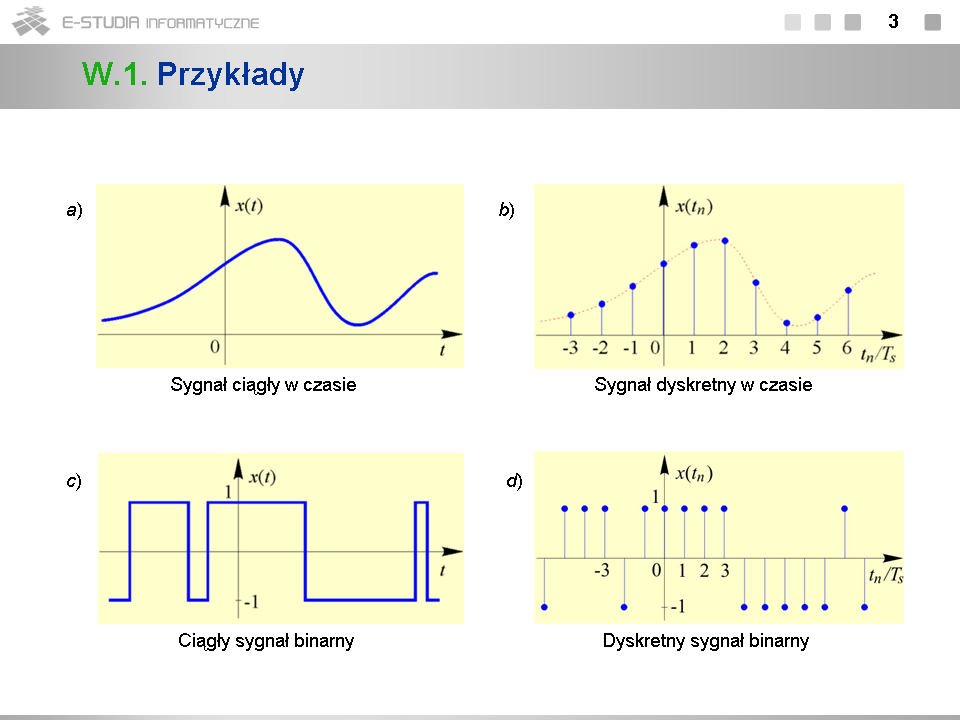
*Zwróćmy uwagę, że sygnały przedstawione na rys. b) i d) otrzymujemy w wyniku próbkowania sygnałów z rys. a) i odpowiednio c). Z sygnałami powstałymi w wyniku próbkowania sygnałów analogowych mamy w praktyce do czynienia najczęściej. Sygnałami dyskretnymi mogą być jednak także sygnały nie mające pierwowzorów analogowych, np. ciąg notowań dziennych kursu złotówki do dolara. Podkreślmy, że sygnał dyskretny jest w istocie rzeczy ciągiem liczb. | |||
*Sygnały analogowe będziemy oznaczać <math>x(t)\,</math> , <math>y(t),\,...\,</math> , zaś sygnały dyskretne – <math>x(t_n)\,</math> , <math>y(t_n),\,...\,</math> lub w przypadku próbkowania równomiernego w chwilach <math>nT_s-x(nT_s)\,</math> , <math>y(nT_s)\,...\,</math> W odniesieniu do tych ostatnich z reguły operuje się czasem bezwymiarowym, unormowanym względem okresu próbkowania <math>T_s\,</math> . Oznacza się je wówczas symbolami <math>x[n]\,</math> , <math>y[n],\,...\,</math> lub <math>x(n)\,</math> , <math>y(n),\,...\,</math> , gdzie <math>n\epsilon jest numerem próbki.</math> | |||