TC Moduł 2

---

Zasygnalizowany w poprzednim wykładzie proces minimalizacji funkcji boolowskich ma ogromne znaczenie w technice cyfrowej. Znaczenie to zostało spotęgowane możliwościami realizacji układów logicznych w strukturach scalonych o złożoności milionów bramek logicznych.

---

Wypracowano wiele metod minimalizacji funkcji boolowskich. Najbardziej znaną i uznawaną za najskuteczniejszą jest metoda ESPRESSO opracowana w latach 80. na Uniwersytecie Kalifornijskim w Berkeley. Ze względu na ograniczony zakres wykładu omówimy wyłącznie metodę tablic Karnaugha oraz metodę ekspansji (przykładową procedurę Espresso).

---

W metodzie Karnaugha każda kratka odpowiedniej tablicy (zwanej tablicą Karnaugha) odpowiada wektorowi zmiennych binarnych. Można więc powiedzieć, że ciąg wartości tych zmiennych tworzy adres kratki. Kratki są ponumerowane w taki sposób, że numer $i$ jest liczbą dziesiętną odpowiadającą kombinacji zmiennych (wektorowi zero-jedynkowemu) traktowanej jako liczba dwójkowa. W poszczególnych kratkach wpisane są wartości funkcji, tj. 0 lub 1 przyjmowanej przez funkcję dla tej kombinacji lub symbol „–”, jeżeli funkcja nie jest określona. W tablicy K. różniącym się tylko o negację pełnym iloczynom przyporządkowane są leżące obok siebie pola tablicy (sąsiednie kratki), które się łączy (skleja) odpowiednią pętelką. Korzysta się z faktu, że dla dowolnego A: $A\overline{x}+Ax=A$

---

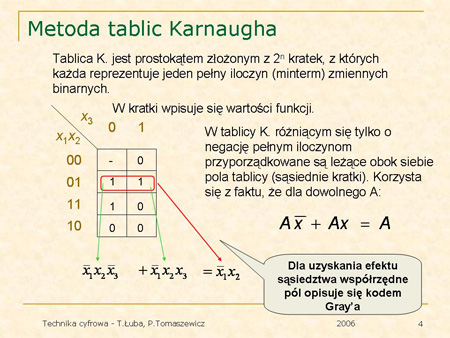
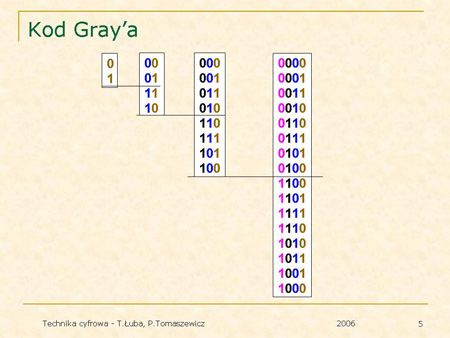
Dla uzyskania efektu sąsiedztwa współrzędne pól opisuje się tzw. kodem Gray’a.

---

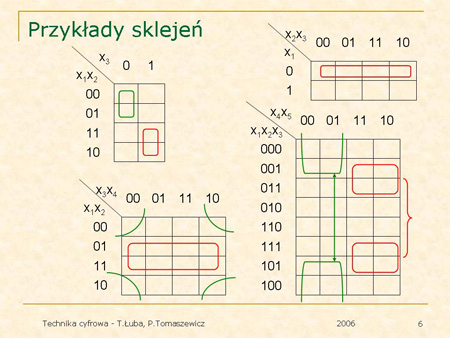
Na planszy pokazane są przykłady łączenia (sklejania) kratek tablicy Karnaugha.

---

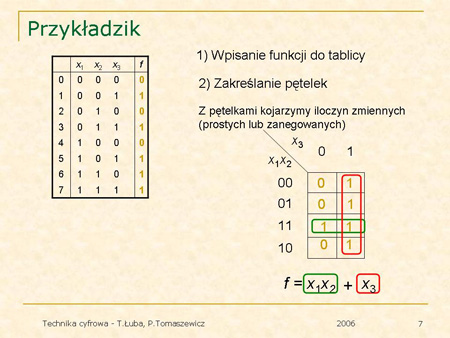
Kolejny przykłady ilustruje wykorzystanie zasady łączenia kratek do graficznej minimalizacji funkcji boolowskiej.

---

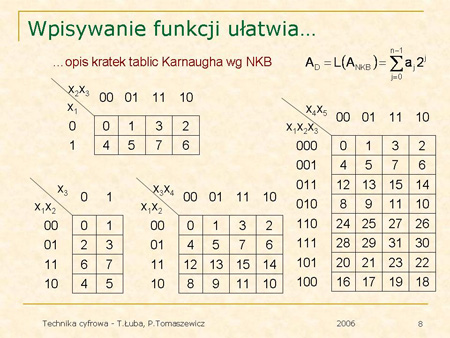
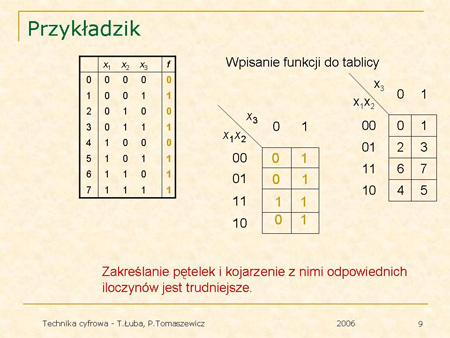
Wpisywanie funkcji do tablicy Karnaugha ułatwia numeracja kratek. Podajemy przykłady tablic Karnaugha z ponumerowanymi kratkami.

---

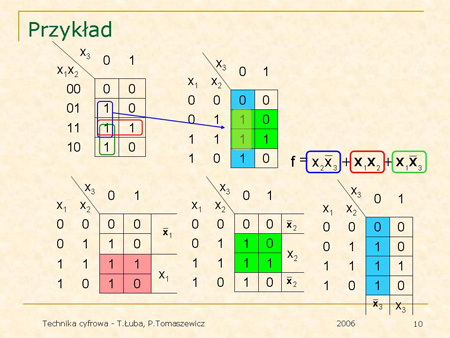
Oraz stosujemy tę metodę do funkcji z poprzedniego przykładu.

---

Niestety zakreślanie pętelek i kojarzenie z nimi odpowiednich iloczynów jest trudniejsze. Omawiamy ten proces na bardziej skomplikowanym przykładzie, w którym kolorami zaznaczamy odpowiednie pola tablicy Karnaugha. Pokrywanie się tych pól określa odpowiedni iloczyn zmiennych prostych lub zanagowanych.

---

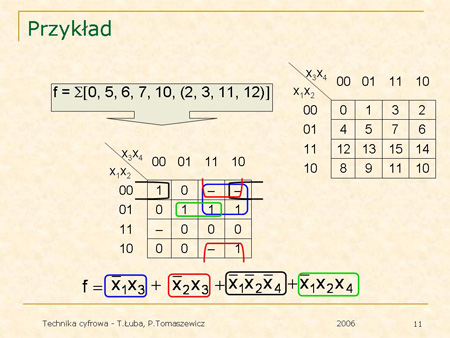
Na tym przykładzie trenujemy cały proces minimalizacji funkcji metodą tablic Karnaugha

---

Pojęciem podstawowym w procesie minimalizacji jest pojęcie implikantu. Implikant funkcji boolowskiej $f$ jest to iloczyn literałów (czyli zmiennych prostych lub zanegowanych) o następującej własności: dla wszystkich kombinacji wartości zmiennych, dla których implikant jest równy jedności, również funkcja $f$ jest równa jedności. Prosty implikant jest to implikant, który zmniejszony o dowolny literał przestaje być implikantem.

---

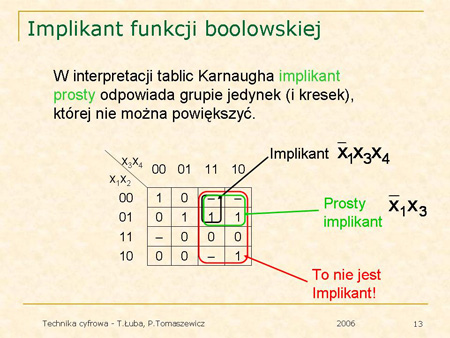
Pojęcie implikantu można zinterpretować na tablicy Karnaugha.

---

Omówimy teraz zapis funkcji boolowskiej w kanonicznej formie sumacyjnej oraz kanonicznej formie iloczynowej.

---

Podajemy ogólny wzór na kanoniczną formę sumacyjną oraz sposób tworzenia tej formy dla przykładowej funkcji. KFS można utworzyć bezpośrednio z tablicy prawdy przez wybranie wierszy, dla których wartość funkcji wynosi 1, utworzenie dla każdego takiego wiersza iloczynu pełnego, oraz utworzenie sumy iloczynów pełnych.

---

Podajemy ogólny wzór na kanoniczną formę iloczynową oraz sposób tworzenia tej formy dla przykładowej funkcji. W tym przypadku synteza funkcji sprowadza się do wybrania wierszy, dla których wartość funkcji wynosi 0, utworzenia dla każdego takiego wiersza sumy pełnej oraz utworzenia iloczynu sum pełnych.

---

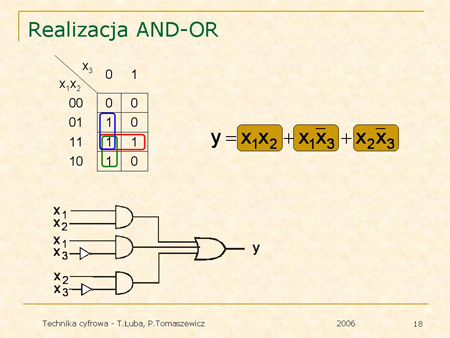
Formy kanoniczne są stosowane do uzyskiwania różnych realizacji bramkowych funkcji boolowskich. Są to: realizacja AND-OR, realizacja NAND, realizacja OR-AND, realizacja NOR.

---

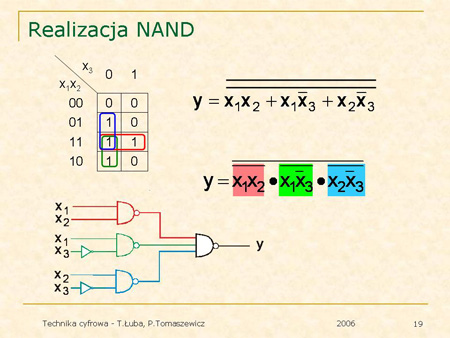
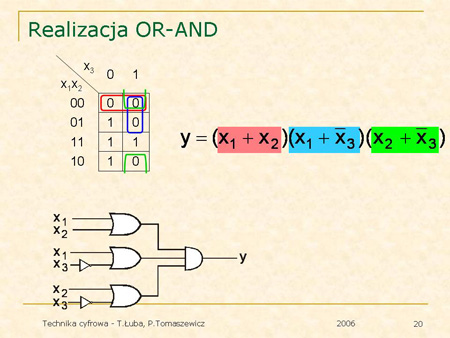
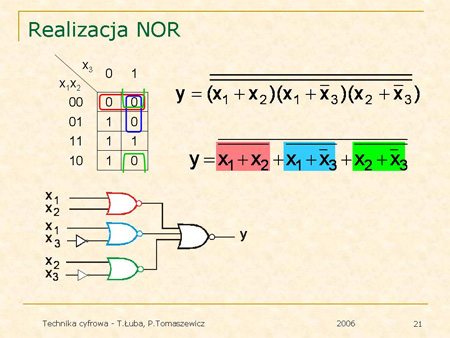
Kolejne plansze ilustrują sposób tworzenia takich realizacji.

---

---

---

---

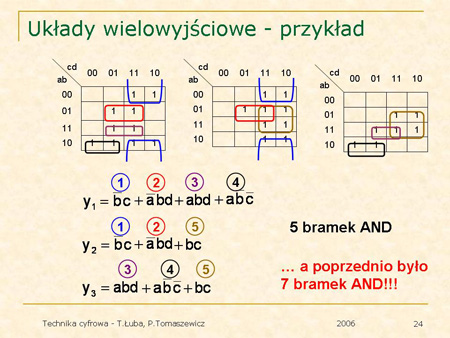
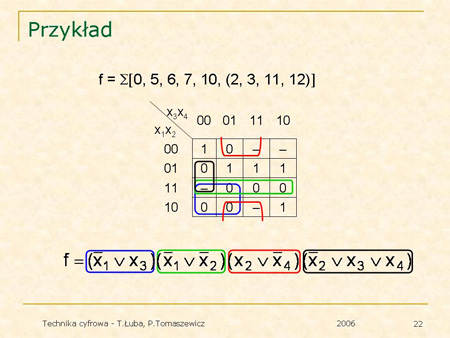
Oto bardziej skomplikowany przykład realizacji iloczynowej.

---

W dotychczasowych przykładach minimalizowane były pojedyncze funkcje boolowskie, dla których – w celu uzyskania rozwiązania z minimalnym kosztem – tworzone były wyłącznie implikanty proste. W ogólnym przypadku minimalizacji zespołów funkcji boolowskich tworzenie minimalnego rozwiązania wyłącznie na podstawie implikantów prostych nie zawsze prowadzi do najlepszego rezultatu końcowego. Poniższy przykład ilustruje w jaki sposób należy dobierać implikanty zespołu funkcji, aby uzyskać rozwiązanie z minimalnym kosztem.

---

Jak widać realizacja powyższych wyrażeń łącznie, mimo pozornie większego skomplikowania dla poszczególnych funkcji, jest oszczędniejsza niż poprzednio; całość wymaga bowiem zastosowania 5 bramek AND i trzech bramek OR.