PEE Zadania z rozwiązaniami: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
'''Zadanie 2''' | '''Zadanie 2''' | ||
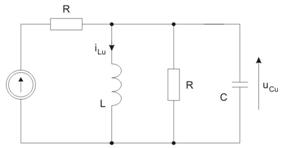
Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci <math>V_1\,</math> i <math>V_2\,</math>. Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: <math>i_1(t)=10\sqrt{2}\sin(\omega t)</math>, <math>i_2(t)=5\sqrt{2}\sin(\omega t-90^\circ)</math>, <math>e_1(t)=10\sin(\omega t+45^\circ)</math>, <math>e_2(t)=20\sin(\omega t+90^\circ)</math>, <math>R=2\Omega</math>, <math>X_L=\omega L=2\Omega</math>, <math>X_C=1/\omega C=1\Omega</math> | Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci <math>V_1\,</math> i <math>V_2\,</math>. Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: <math>i_1(t)=10\sqrt{2}\sin(\omega t)</math>, <math>i_2(t)=5\sqrt{2}\sin(\omega t-90^\circ)</math>, <math>e_1(t)=10\sin(\omega t+45^\circ)</math>, <math>e_2(t)=20\sqrt{2}\sin(\omega t+90^\circ)</math>, <math>R=2\Omega</math>, <math>X_L=\omega L=2\Omega</math>, <math>X_C=1/\omega C=1\Omega</math> | ||
[[Grafika:PEE_Zadania_rozw_2.jpg]] | [[Grafika:PEE_Zadania_rozw_2.jpg]] | ||
| Linia 131: | Linia 131: | ||
Wielkości symboliczne charakteryzujące elementy obwodu: | Wielkości symboliczne charakteryzujące elementy obwodu: | ||
: <math>I={ | : <math>I={10 \over \sqrt{2}}e^{j45^\circ}</math> | ||
: <math>Z_1=j\omega(L_1-M)=j1</math> | : <math>Z_1=j\omega(L_1-M)=j1</math> | ||
: <math>Z_2=j\omega(L_2-M)=0</math> | : <math>Z_2=j\omega(L_2-M)=0</math> | ||
| Linia 213: | Linia 213: | ||
Wobec <math>\omega=0</math> kondensator stanowi przerwę. Prąd płynie w obwodzie: <math>e-R_1-R_1</math>. Jego wartość: | Wobec <math>\omega=0</math> kondensator stanowi przerwę. Prąd płynie w obwodzie: <math>e-R_1-R_1</math>. Jego wartość: | ||
: <math>I={e \over 2R_1}={20 \over 200}=0,1 | : <math>I={e \over 2R_1}={20 \over 200}=0,1</math> | ||
Napięcie na kondensatorze: | Napięcie na kondensatorze: | ||
: <math> | : <math>U_{R1}=10</math> | ||
: <math>u_C(0^-)= | : <math>u_C(0^-)=10</math> | ||
| Linia 225: | Linia 225: | ||
Obwód podobny do tego z punktu 1 przy zastąpieniu <math>R_1\,</math> przez <math>R_2\,</math>. Prąd płynie w obwodzie: <math>e-R_1-R_2</math>. Jego wartość: | Obwód podobny do tego z punktu 1 przy zastąpieniu <math>R_1\,</math> przez <math>R_2\,</math>. Prąd płynie w obwodzie: <math>e-R_1-R_2</math>. Jego wartość: | ||
: <math>I={e \over R_1+R_2}={20 \over 400}={1 \over 20} | : <math>I={e \over R_1+R_2}={20 \over 400}={1 \over 20}</math> | ||
Napięcie ustalone na kondensatorze: | Napięcie ustalone na kondensatorze: | ||
: <math>u_{C_u}(t)=IR_2= | : <math>u_{C_u}(t)=IR_2=15</math> | ||
| Linia 325: | Linia 325: | ||
Prąd kondensatora | Prąd kondensatora | ||
: <math>i_{c_p}=C{du_{C_p} \over dt}=0,85[e^{-t}-te^{-t}]+1,41e^{-t}=2,26e^{-t}-0,85te^{-t}</math> | : <math>i_{c_p}(t)=C{du_{C_p} \over dt}=0,85[e^{-t}-te^{-t}]+1,41e^{-t}=2,26e^{-t}-0,85te^{-t}</math> | ||
Prąd rezystora | Prąd rezystora | ||
: <math>i_{R_p}={u_{C_p} \over R}=1,7te^{-t}-2,82e^{-t}</math> | : <math>i_{R_p}(t)={u_{C_p} \over R}=1,7te^{-t}-2,82e^{-t}</math> | ||
Prąd cewki | Prąd cewki | ||
| Linia 382: | Linia 382: | ||
Dane: | Dane: | ||
: <math> | : <math>R_1 = 2 \Omega</math> | ||
: <math> | : <math>R_2 = 5 \Omega</math> | ||
: <math>C = 0,5 F</math> | : <math>C = 0,5 F</math> | ||
: <math>L = 1 H</math> | : <math>L = 1 H</math> | ||
| Linia 428: | Linia 428: | ||
Transmitancja napięciowa obliczana przy założeniu <math>I_2 = 0</math>: | Transmitancja napięciowa obliczana przy założeniu <math>I_2 = 0</math>: | ||
: <math>I_2=0=-{1 \over s}V_1+(0,2+0,5s)V_2</math> | : <math>I_2=0=-{1 \over s}V_1+(0,2+0,5s+ {1 \over s})V_2</math> | ||
Stąd: | Stąd: | ||
: <math>{V_2 \over V_1}={{1 \over s} \over 0,2+0,5s}</math> | : <math>{V_2 \over V_1}={{1 \over s} \over 0,2+0,5s + {1 \over s}}</math> | ||
: <math>T_v(s)={V_2 \over V_1}={2 \over s | : <math>T_v(s)={V_2 \over V_1}={2 \over s^2+0,4s+2)}</math> | ||
Wersja z 14:01, 25 sie 2006
Zadanie 1
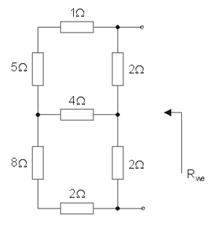
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej:
Rozwiązanie
Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się .
Zadanie 2
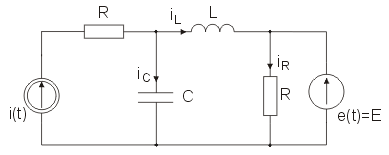
Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci i . Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: , , , , , ,
Rozwiązanie
Wartości zespolone:
Równanie admitancyjne
Z rozwiązania tego macierzowego układu równań mamy
Prądy w obwodzie:
- (prąd rezystora i źródła )
Zadanie 3
Wyznaczyć rozwiązanie obwodu z rysunku poniżej stosując zasadę superpozycji. Przyjąć , , , , , .
Rozwiązanie
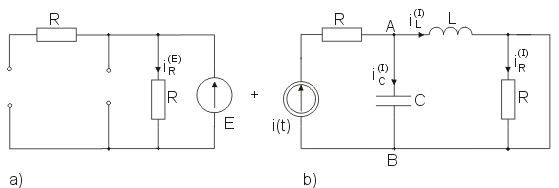
A) Rozwiązanie obwodu dla składowej stałej (źródło )
Obwód dla składowej stałej przedstawiono na rysunku poniżej (a). Cewka w stanie ustalonym dla składowej stałej jest zwarciem a kondensator przerwą.
Dla prądu stałego tylko jeden prąd, , jest różny od zera. Jego wartość jest równa
B) Rozwiązanie obwodu dla składowej zmiennej (źródło )
Obwód dla składowej sinusoidalnej przedstawiono w postaci symbolicznej na (rys. b). Parametry symboliczne obwodu są następujące: , , . Impedancja zastępcza cewki i kondensatora jest równa
Napięcie i prądy w obwodzie:
Wartości prądów wyrażone w postaci czasowej:
Całkowite rozwiązanie obwodu jest sumą obu składowych:
Zadanie 4
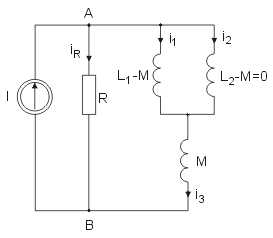
Wyznaczyć rozpływy prądów w obwodzie przedstawionym poniżej:
Przyjąć następujące wartości parametrów elementów obwodu: , , , oraz
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono poniżej:
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
Napięcie
Prądy:
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą . Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie
Zadanie 5
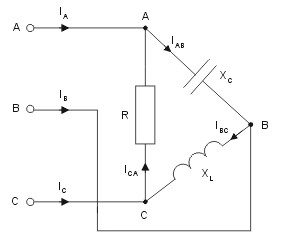
Wyznaczyć prądy w układzie trójfazowym o odbiorniku połączonym w trójkąt przedstawionym na rysunku poniżej. Sporządzić wykres wektorowy prądów i napięć. Przyjąć następujące wartości parametrów elementów: , .
Rozwiązanie
Napięcia międzyfazowe:
Prądy fazowe odbiornika:
Prądy liniowe układu:
Wykres wektorowy prądów i napięć przedstawiony jest poniżej:
Zadanie 6
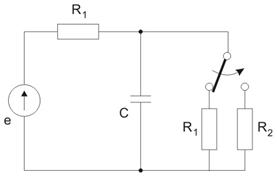
Określić przebieg w stanie nieustalonym w obwodzie po przełączeniu.
Dane:
Rozwiązanie
1) Warunki początkowe w obwodzie (stan ustalony przed przełączeniem).
Wobec kondensator stanowi przerwę. Prąd płynie w obwodzie: . Jego wartość:
Napięcie na kondensatorze:
2) Stan ustalony w obwodzie po przełączeniu.
Obwód podobny do tego z punktu 1 przy zastąpieniu przez . Prąd płynie w obwodzie: . Jego wartość:
Napięcie ustalone na kondensatorze:
3) Stan przejściowy (metoda klasyczna).
Obwód dla stanu przejściowego pokazuje rysunek:
Z prawa prądowego Kirchhoffa:
Po wstawieniu liczb otrzymuje się
4) Rozwiązanie pełne
Z warunku początkowego
Przebieg napięcia
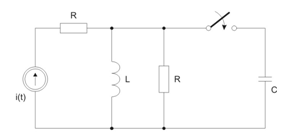
Zadanie 7
Wyznaczyć przebiegi oraz w stanie nieustalonym w obwodzie po przełączeniu.
Dane:
Rozwiązanie
Warunki początkowe – stan ustalony w obwodzie przed przełączeniem
Stan ustalony po przełączeniu
Stan przejściowy
Warunki początkowe dla stanu przejściowego
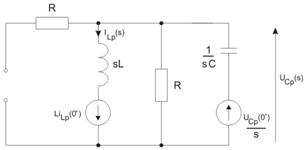
Obwód w stanie przejściowym (schemat operatorowy)
Z metody potencjałów węzłowych
Prąd kondensatora
Prąd rezystora
Prąd cewki
Pełne rozwiązanie
Zadanie 8
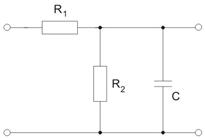
Wyznaczyć transmitancję napięciową układu przedstawionego na rysunku poniżej. Określić odpowiedź impulsową i skokową.
Dane:
Rozwiązanie
Impedancja zastępcza :
Transmitancja napięciowa:
Odpowiedź impulsowa:
Odpowiedź skokowa:
Zadanie 9
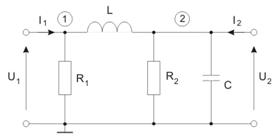
Określić opis admitancyjny czwórnika. Na tej podstawie określić transmitancję napięciową obwodu.
Dane:
Rozwiązanie
Z równań węzłowych obwodu względem punktu odniesienia mamy:
Transmitancja napięciowa obliczana przy założeniu :
Stąd: