PEE Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 283: | Linia 283: | ||
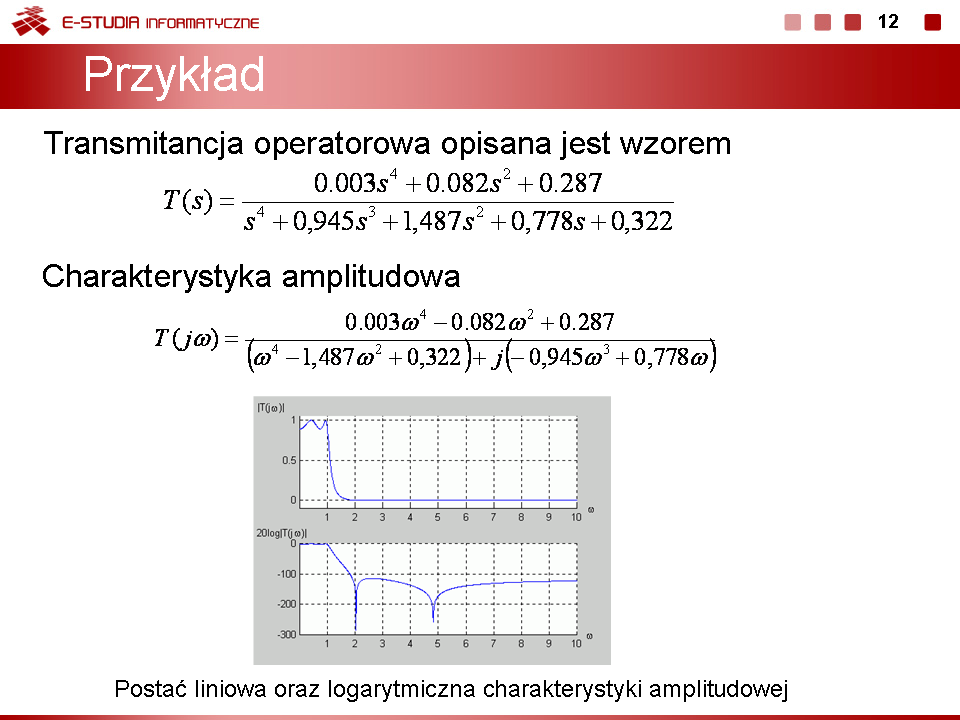
Charakterystyka amplitudowa wskazuje na dobre (nie tłumione) przenoszenie częstotliwości małych. W miarę wzrostu wartości częstotliwości charakterystyka amplitudowa maleje, co oznacza, że sygnał wyjściowy ma coraz mniejszą amplitudę. Taki obwód ma więc charakter układu dolnoprzepustowego (szeregowo włączona cewka w miarę wzrostu częstotliwości ma coraz większą impedancję tłumiącą przebieg prądu przepływającego przez rezystor wyjściowy). | Charakterystyka amplitudowa wskazuje na dobre (nie tłumione) przenoszenie częstotliwości małych. W miarę wzrostu wartości częstotliwości charakterystyka amplitudowa maleje, co oznacza, że sygnał wyjściowy ma coraz mniejszą amplitudę. Taki obwód ma więc charakter układu dolnoprzepustowego (szeregowo włączona cewka w miarę wzrostu częstotliwości ma coraz większą impedancję tłumiącą przebieg prądu przepływającego przez rezystor wyjściowy). | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd13.png]] | |||
|valign="top"|'''Przykłady transmitancji operatorowych pierwszego rzędu''' | |||
W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. | |||
'''Układ całkujący''' | |||
Transmitancja idealnego układu całkującego definiowana jest w postaci | |||
: <math>T(s)=\frac{k}{s}</math> | |||
Układ nosi nazwę całkującego, gdyż operator 1/s w dziedzinie częstotliwości zespolonej Laplace’a oznacza całkowanie funkcji w dziedzinie czasu. Charakterystykę częstotliwościową układu całkującego opisuje zależność | |||
: <math>T(j\omega)=\frac{k}{j\omega}=\frac{k}{\omega}e^{-j90^\circ}</math> | |||
Wykres charakterystyki amplitudowej | |||
: <math>|T(j\omega)|=\frac{k}{\omega}</math> | |||
oraz fazowej | |||
: <math>\varphi(\omega)=-90^\circ</math> | |||
dla układu całkującego przy k>0 przedstawiono na slajdzie 13. | |||
Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe <math>-90^\circ</math> niezależnie od częstotliwości). | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 22:18, 1 sie 2006

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |

|
Na slajdzie 9 przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s). |