PEE Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 229: | Linia 229: | ||
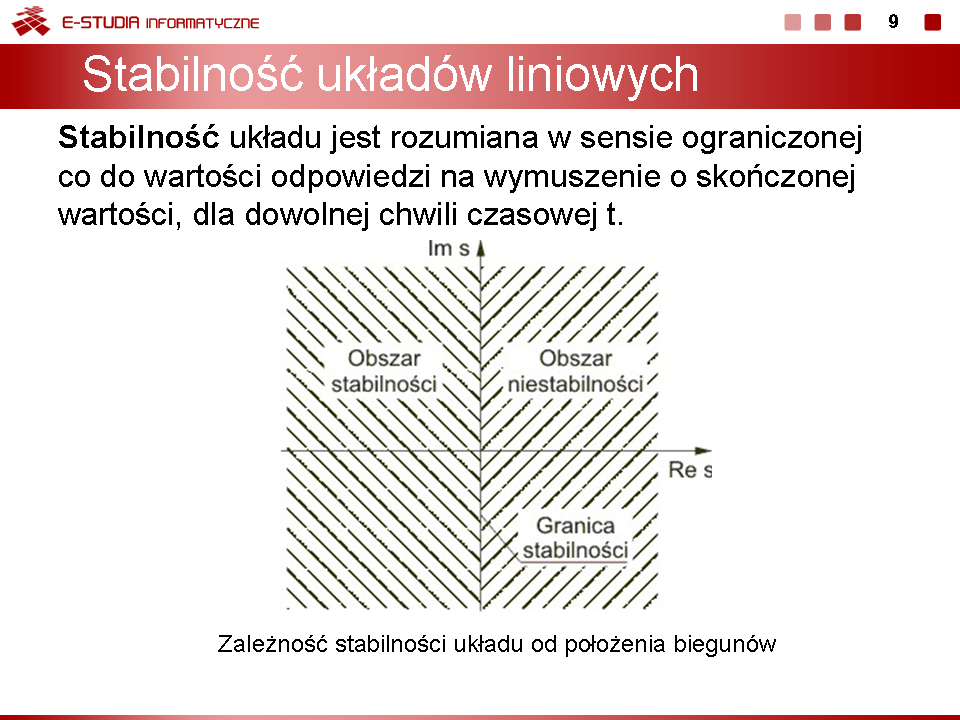
|valign="top"|Na slajdzie 9 zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | |valign="top"|Na slajdzie 9 zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | ||
Interesujący jest również wpływ położenia biegunów na charakter odpowiedzi impulsowej układu liniowego. | Interesujący jest również wpływ położenia biegunów na charakter odpowiedzi impulsowej układu liniowego. Slajd 10 przedstawia odpowiedzi impulsowe układu drugiego rzędu przy różnych położeniach biegunów. | ||
W zależności od wartości biegunów mamy do czynienia ze stanem aperiodycznym (bieguny położone na osi rzeczywistej) oraz oscylacyjnym (bieguny zespolone). Zanikanie odpowiedzi impulsowej do zera świadczy o stabilności asymptotycznej układu. Odpowiedź o ograniczonej amplitudzie nie zanikająca z czasem świadczy o stabilności zwykłej układu. Odpowiedź narastająca z czasem jest cechą układu niestabilnego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd11.png]] | |||
|valign="top"|'''Charakterystyki częstotliwościowe układów''' | |||
Charakterystyką częstotliwościową układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę '''transmitancji widmowej''' układu. | |||
Oznaczmy transmitancję widmową w postaci <math>T(j \omega)</math>. Jest ona zdefiniowana jako transmitancja operatorowa dla <math>s=j \omega</math>, to znaczy | |||
: <math>T(j\omega)=T(s)|_{s=j\omega}</math> | |||
Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji <math>\omega\,</math>. Przedstawiając ją w postaci wykładniczej, to jest <math>T(j\omega)=|T(j\omega)|e^{j\varphi (\omega)}</math> można zdefiniować dwa rodzaje charakterystyk częstotliwościowych: | |||
* '''charakterystyka amplitudowa''' przedstawia sobą zależność modułu transmitancji widmowej <math>T(j\omega)</math> od pulsacji <math>\omega\,</math> (częstotliwości f), to jest <math>|T(j\omega)|</math> | |||
* '''charakterystyka fazowa''' określa zależność argumentu transmitancji widmowej <math>T(j\omega)</math> od pulsacji (częstotliwości) to jest <math>\varphi (\omega)</math>. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji <math>\omega\,</math>. | |||
Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\,</math> do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | |||
: <math>20log_{10}(|T(j\omega)|)</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd12.png]] | |||
|valign="top"|''Przykład'' | |||
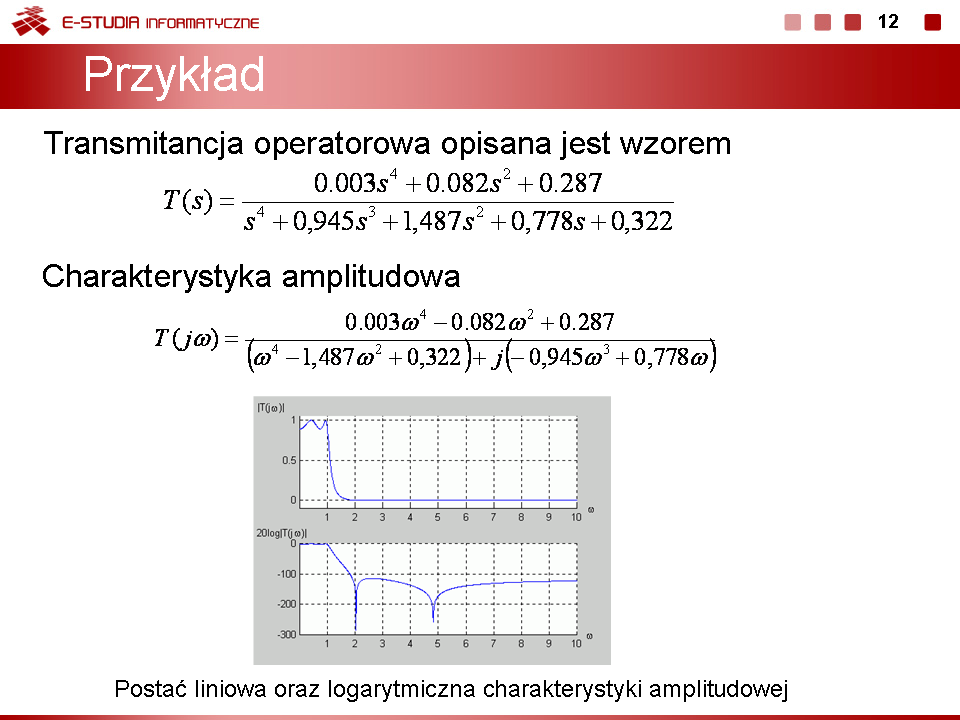
Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem | |||
<math>T(s)=\frac{0,003s^4+0,082s^2+0,287}{s^4+0,945s^3+1,487s^2+0,778s+0,322}</math> | |||
Charakterystyka amplitudowa jest określona wzorem | |||
<math>T(s)=\frac{0,003\omega^4-0,082\omega^2+0,287}{(\omega^4-1,487\omega^2+0,322)+j(-0,945\omega^3+0,778\omega)}</math> | |||
Na slajdzie 12 przedstawiono przykładowo charakterystykę amplitudową oraz logarytmiczną charakterystykę amplitudową odpowiadającą transmitancji danej wzorem | |||
Każdy rodzaj przedstawienia charakterystyki amplitudowej podkreśla inne szczegóły w jej przebiegu. Charakterystyka logarytmiczna podkreśla stosunkowo niewielkie w skali globalnej zmiany dynamiczne w tak zwanym paśmie zaporowym, gdzie amplituda sygnału jest bardzo mała w stosunku do pasma przepustowego, podczas gdy skala liniowa uwypukla globalny charakter przebiegu tracąc drobne szczegóły w zakresie częstotliwości gdzie wartości sygnałów są małe. | |||
Charakterystyka amplitudowa wskazuje na dobre (nie tłumione) przenoszenie częstotliwości małych. W miarę wzrostu wartości częstotliwości charakterystyka amplitudowa maleje, co oznacza, że sygnał wyjściowy ma coraz mniejszą amplitudę. Taki obwód ma więc charakter układu dolnoprzepustowego (szeregowo włączona cewka w miarę wzrostu częstotliwości ma coraz większą impedancję tłumiącą przebieg prądu przepływającego przez rezystor wyjściowy). | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 22:06, 1 sie 2006

|
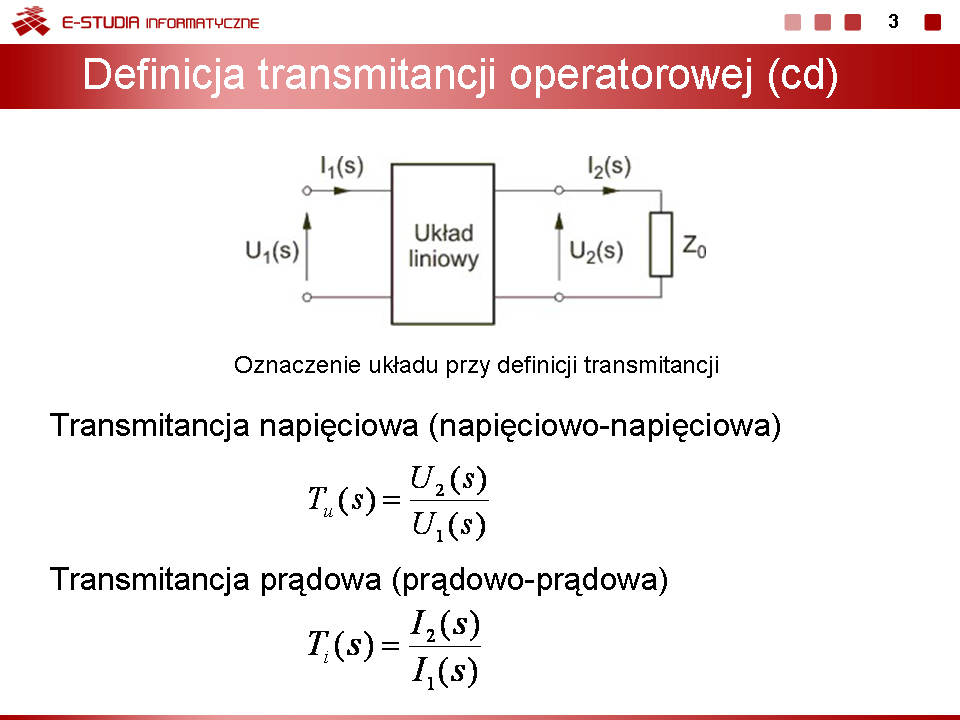
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |

|
Na slajdzie 9 przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s). |