MN04LAB: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „<math> ” na „<math>” |
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
||
| Linia 85: | Linia 85: | ||
<center><math>|fl_\nu(\|A x\|_2)-\|A x\|_2|\,\leq\,2(n+2)\sqrt{n}\,\nu\, | <center><math>|fl_\nu(\|A x\|_2)-\|A x\|_2|\,\leq\,2(n+2)\sqrt{n}\,\nu\, | ||
\left(\|A\|_2\|A^{-1}\|_2\right)\,\|A x\|_2 | \left(\|A\|_2\|A^{-1}\|_2\right)\,\|A x\|_2</math></center> | ||
</math></center> | |||
</div></div> | </div></div> | ||
| Linia 125: | Linia 124: | ||
Ponieważ nasze zadanie to wyznaczenie <math>x^* = f^{-1}(0)</math>, to | Ponieważ nasze zadanie to wyznaczenie <math>x^* = f^{-1}(0)</math>, to | ||
<center><math> | <center><math> | ||
\mbox{cond} _{abs} (f^{-1},0) = \frac{1}{f'(x^*)} | \mbox{cond} _{abs} (f^{-1},0) = \frac{1}{f'(x^*)}</math></center> | ||
</math></center> | |||
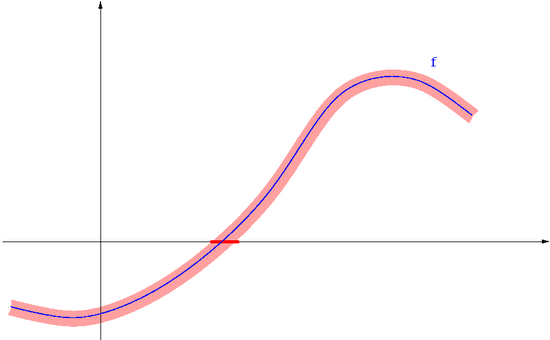
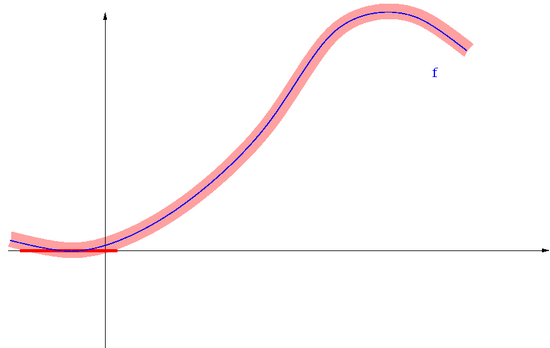
Znaczy to, że im bardziej płaska jest <math>f</math> w otoczeniu pierwiastka <math>x^*</math>, tym | Znaczy to, że im bardziej płaska jest <math>f</math> w otoczeniu pierwiastka <math>x^*</math>, tym | ||
Wersja z 21:34, 11 wrz 2023
Uwarunkowanie zadania i algorytmy numerycznie poprawne.
<<< Powrót do strony głównej przedmiotu Metody numeryczne
Oglądaj wskazówki i rozwiązania __SHOWALL__
Ukryj wskazówki i rozwiązania __HIDEALL__
Ćwiczenie
Aby obliczyć można zastosować dwa algorytmy: oraz . Pokazać, że oba algorytmy są numerycznie poprawne, ale drugi z nich wywołuje mniejszy błąd względny wyniku w przypadku, gdy i .
Rozwiązanie
Ćwiczenie
Pokazać, że naturalny algorytm obliczania cosinusa kąta między dwoma wektorami ,
jest numerycznie poprawny. Oszacować błąd względny wyniku w .
Ćwiczenie
Podaj przykład funkcji , której miejsce zerowe ma wspólczynnik uwarunkowania
- mały
- duży
Rozwiązanie