CWGI Ćwiczenie 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ </math>” na „</math>” |
m Zastępowanie tekstu – „,</math>” na „</math>” |
||
| Linia 51: | Linia 51: | ||
|valign="top"|Krawędzie poszczególnych par płaszczyzn oznaczymy kolejno: | |valign="top"|Krawędzie poszczególnych par płaszczyzn oznaczymy kolejno: | ||
<math>k_1=\alpha \cap \beta\ | <math>k_1=\alpha \cap \beta\</math>, <math>k_2=\beta \cap \gamma\</math>, <math>k_3=\alpha \cap \gamma\</math> | ||
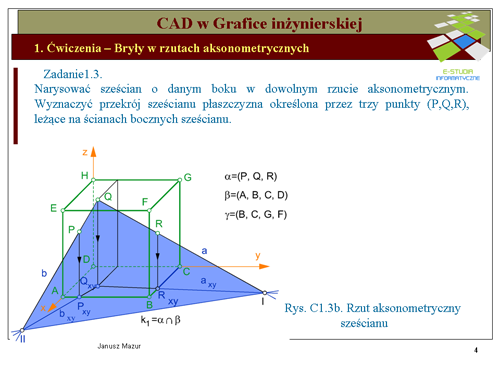
Wyznaczając konstrukcyjnie krawędzie <math>k_1\ | Wyznaczając konstrukcyjnie krawędzie <math>k_1\</math> i <math>k_2\</math>, możemy następnie, korzystając z twierdzenia o punkcie wspólnym trójki płaszczyzn, wyznaczyć poszukiwaną w zadaniu krawędź <math>k_3\</math>. | ||
'''Wyznaczanie krawędzi <math>k_1\ | '''Wyznaczanie krawędzi <math>k_1\</math>''' | ||
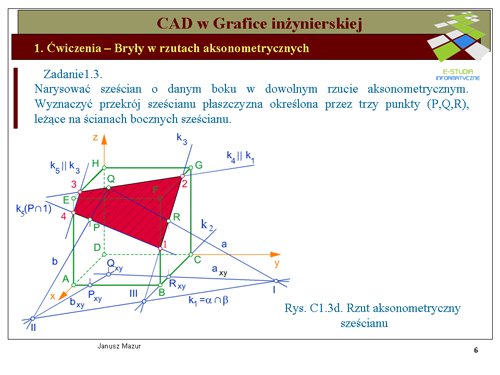
Poprowadźmy dwie proste należące do płaszczyzny <math>\alpha (PQR)\ | Poprowadźmy dwie proste należące do płaszczyzny <math>\alpha (PQR)\</math>: prostą <math>a\</math>, przechodzącą przez punkty <math>Q\</math>,, <math>R\</math>, oraz prostą b przechodzącą przez punkty <math>Q\</math>,, <math>P\</math>,. Proste te przecinają się w punkcie <math>Q\</math>,. Rzuty <math>a_{xy}\</math> i <math>b_{xy}\</math> tych prostych na płaszczyznę podstawy <math>\beta (ABCD)\</math>, będą przecinały się w punkcie <math>Q_{xy}\</math>. Proste <math>a\</math> i <math>a_{xy}\</math> przecinają się w punkcie oznaczonym cyfrą <math>I\</math>,. Punkt <math>I\</math>, jest, zatem wspólnym dla płaszczyzn <math>\alpha\</math> i <math>\beta\</math>, ponieważ należy do prostych <math>a\</math> i <math>a_{xy}\</math>, a te z kolei należą odpowiednio do płaszczyzn <math>\alpha\</math> i <math>\beta\</math>. Drugi punkt <math>II\</math>, wspólny płaszczyzn <math>\alpha\</math> i <math>\beta\</math> wyznaczymy prowadząc dwie, należące odpowiednio do płaszczyzn <math>\alpha \cap \beta\</math>, kolejne proste <math>b\</math> i <math>b_{xy}\</math> które przetną się właśnie w tym punkcie. Łącząc punkty <math>I\</math>, i <math>II\</math>, wyznaczymy pierwsza z poszukiwanych krawędzi <math>k_1 =\alpha \cap \beta\</math>. Jak widać na rysunku C1.3b krawędź <math>k_1\</math> leży na płaszczyźnie <math>\beta (ABCD)\</math>,, lecz nie przecina ściany <math>ABCD\</math>, sześcianu. | ||
|} | |} | ||
| Linia 69: | Linia 69: | ||
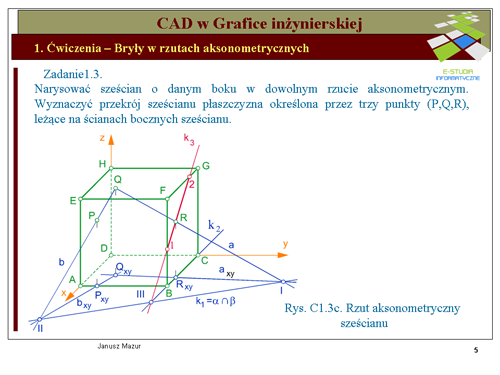
'''Wyznaczanie krawędzi <math>k_2\ | '''Wyznaczanie krawędzi <math>k_2\</math>''' | ||
Krawędź <math>k_2\ | Krawędź <math>k_2\</math> wyznaczymy w sposób natychmiastowy, albowiem stanowi ona wspólną krawędź ścian <math>ABCD\</math>, oraz <math>BCFG\</math>, sześcianu. | ||
'''Wyznaczanie krawędzi <math>k_3\ | '''Wyznaczanie krawędzi <math>k_3\</math>''' | ||
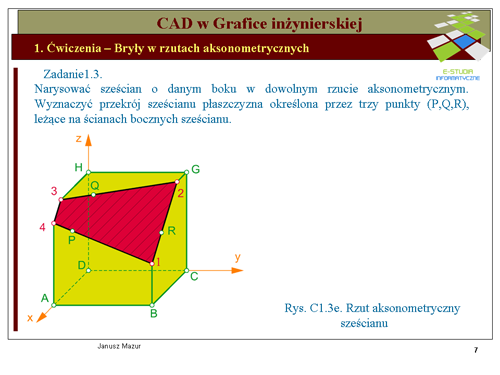
Krawędź <math>k_2\ | Krawędź <math>k_2\</math> przecina krawędź <math>k_1\</math> w punkcie oznaczonym cyfrą <math>III\</math>,. Punkt <math>III\</math>, jest, zatem punktem '''''wspólnym trójki płaszczyzn''''' <math>\alpha\</math>,, <math>\beta\</math>, i <math>\gamma\</math>,. Przez ten punkt, zgodnie z cytowanym wcześniej twierdzeniem, będzie przechodziła trzecia krawędź <math>k_3=\alpha \cap \gamma\</math>. Drugi punkt wspólny tych płaszczyzn jest punktem <math>R\</math>, (z założenia punkt należący do płaszczyzny <math>\alpha\</math>, i <math>\beta\</math>,). Punkty <math>III\</math>, i <math>R\</math>, wyznaczą nam poszukiwaną krawędź <math>k_3\</math>,, która jest krawędzią przekroju płaszczyzny <math>\alpha\</math>, z jedną ze ścian sześcianu. Krawędź <math>k_3\</math>, przecina krawędzie sześcianu: <math>BF\</math>, w punkcie <math>1\</math>, oraz <math>CG\</math>, w punkcie <math>2\</math>,. Punkty te wyznaczają odcinek będący krawędzią przekroju ściany <math>BCGF\</math>, sześcianu płaszczyzną <math>\alpha\</math>,. | ||
|} | |} | ||