Analiza matematyczna 2/Ćwiczenia 12: Całka krzwoliniowa. Twierdzenie Greena: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| Linia 131: | Linia 131: | ||
\iint\limits_D-1 dxdy | \iint\limits_D-1 dxdy | ||
= | = | ||
- </math> (pole kwadratu o boku <math>2</math>) <math> | -</math> (pole kwadratu o boku <math>2</math>) <math> | ||
= | = | ||
-4. | -4. | ||
Wersja z 10:07, 5 wrz 2023
Całka krzywoliniowa. Twierdzenie Greena
Ćwiczenie 12.1.
Policzyć
gdzie jest łukiem cykloidy danej parametrycznie:
Ćwiczenie 12.2.
Policzyć
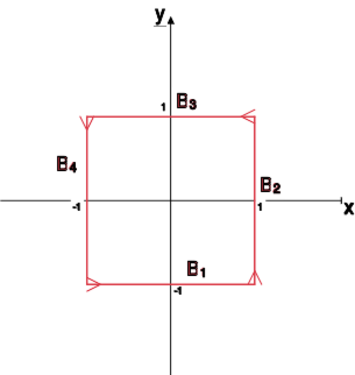
gdzie jest kwadratem o wierzchołkach w obieganym przeciwnie do ruchu wskazówek zegara.
Ćwiczenie 12.3.
W pewnym polu sił składowe pola wynoszą
Policzyć pracę potrzebną do przesunięcia punktu materialnego wzdłuż krzywej łączącej punkt z punktem , danej wzorem .
Ćwiczenie 12.4.
Znaleźć (lub odgadnąć) potencjał dla pola sił z ćwiczenia 12.3.
Ćwiczenie 12.5.
Korzystając z twierdzenia Greena, policzyć
gdzie jest okręgiem środku w i promieniu .
Ćwiczenie 12.6.
Policzyć całkę
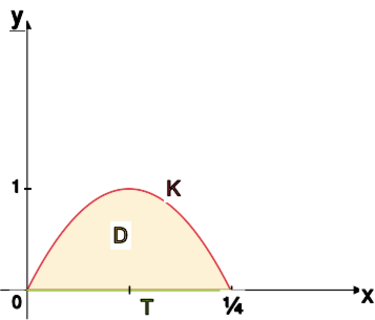
gdzie jest wykresem funkcji , dla .
Ćwiczenie 12.7.
Policzyć całkę krzywoliniową:
gdzie jest parabolą pomiędzy punktami a .
Ćwiczenie 12.8.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone elipsą
gdzie są dane.
Ćwiczenie 12.9.
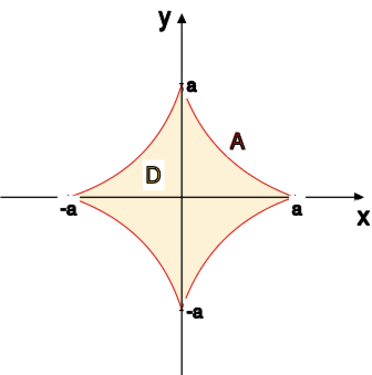
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone asteroidą
gdzie jest dane.