PS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| Linia 125: | Linia 125: | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
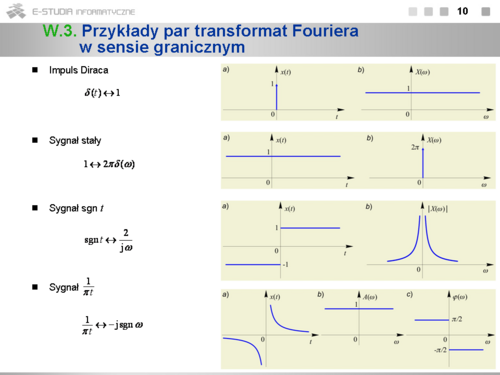
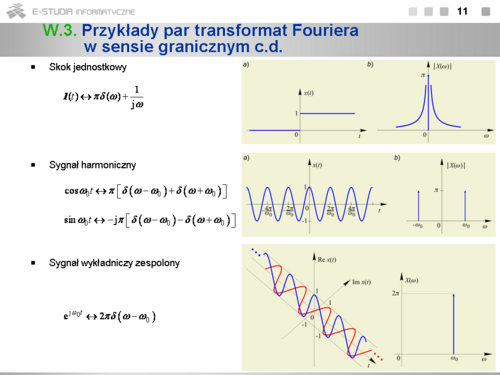
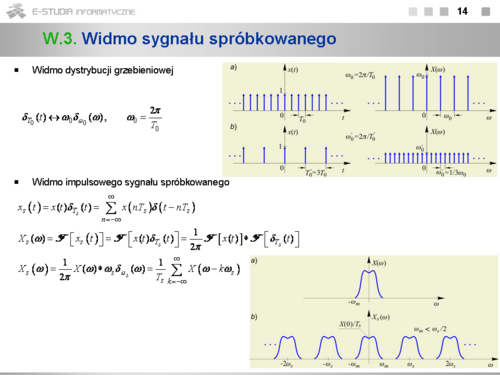
*Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0) </math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\</math>, , <math>k=0,\pm\ 1,...\</math>, , co oddaje jego dyskretny charakter. | *Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0)</math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\</math>, , <math>k=0,\pm\ 1,...\</math>, , co oddaje jego dyskretny charakter. | ||
*Widmo amplitudowe jest ciągiem dystrybucji Diraca w punktach <math>k\omega_0\</math>, i polach <math>2\pi |X_k|\</math>, , zaś widmo fazowe jest ciągiem zwykłych liczb <math>X_k\</math>, . | *Widmo amplitudowe jest ciągiem dystrybucji Diraca w punktach <math>k\omega_0\</math>, i polach <math>2\pi |X_k|\</math>, , zaś widmo fazowe jest ciągiem zwykłych liczb <math>X_k\</math>, . | ||
*Widmo unipolarnej fali prostokątnej z przykładu 3.5 jest ciągiem dystrybucji Diraca, których obwiednią jest funkcja <math>Sa\</math>,. | *Widmo unipolarnej fali prostokątnej z przykładu 3.5 jest ciągiem dystrybucji Diraca, których obwiednią jest funkcja <math>Sa\</math>,. | ||