Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
|||
| Linia 24: | Linia 24: | ||
a) Odwrotnością | a) Odwrotnością | ||
funkcji <math> f</math> jest funkcja | funkcji <math> f</math> jest funkcja | ||
<math> x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2} | <math> x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2}</math>.<br> | ||
b) Wyznaczamy <math> y</math> z równania <math> x=-y+2</math>. Stąd <math> g(x)=-x+2</math> jest | b) Wyznaczamy <math> y</math> z równania <math> x=-y+2</math>. Stąd <math> g(x)=-x+2</math> jest | ||
funkcją odwrotną do <math> f</math>. A więc funkcją odwrotną do <math> f</math> jest | funkcją odwrotną do <math> f</math>. A więc funkcją odwrotną do <math> f</math> jest | ||
| Linia 103: | Linia 103: | ||
Równość <math>g\circ g=f</math> zachodziłaby, gdyby odpowiednie współczynniki homografii <math>g\circ g</math> oraz <math>f</math> były równe, | Równość <math>g\circ g=f</math> zachodziłaby, gdyby odpowiednie współczynniki homografii <math>g\circ g</math> oraz <math>f</math> były równe, | ||
<center><math>0\neq a^2+b=b(a+d)=a+d=-(b+d^2) | <center><math>0\neq a^2+b=b(a+d)=a+d=-(b+d^2)</math>.</center> | ||
Ale jest to niemożliwe, gdyż z równości <math>b(a+d)=a+d</math> wynika, że <math>b=1</math>, co pociąga za sobą w konsekwencji nierówność: <math>1\leq a^2 +1=a^2 | Ale jest to niemożliwe, gdyż z równości <math>b(a+d)=a+d</math> wynika, że <math>b=1</math>, co pociąga za sobą w konsekwencji nierówność: <math>1\leq a^2 +1=a^2 | ||
+b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math>g:\mathbb{R}\mapsto\mathbb{R}</math>, aby <math>g\circ g=f</math>. | +b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math>g:\mathbb{R}\mapsto\mathbb{R}</math>, aby <math>g\circ g=f</math>. | ||
| Linia 138: | Linia 138: | ||
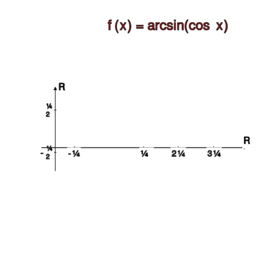
<center><math> \arcsin(\cos | <center><math> \arcsin(\cos | ||
x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x,</math></center> | x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x,</math></center> | ||
dla <math> 0\leq x\leq \pi</math>. Wobec parzystości rozważanej funkcji mamy dla <math> -\pi\leq x\leq\pi</math> równość <center><math> \arcsin(\cos x)=\frac{\pi}{2}-|x| | dla <math> 0\leq x\leq \pi</math>. Wobec parzystości rozważanej funkcji mamy dla <math> -\pi\leq x\leq\pi</math> równość <center><math> \arcsin(\cos x)=\frac{\pi}{2}-|x|</math>.</center> <br> | ||
[[File:an1c02.0020.svg|375x270px|thumb|right|Rysunek do ćwiczenia 2.3.(a)]] | [[File:an1c02.0020.svg|375x270px|thumb|right|Rysunek do ćwiczenia 2.3.(a)]] | ||
| Linia 180: | Linia 180: | ||
funkcji | funkcji | ||
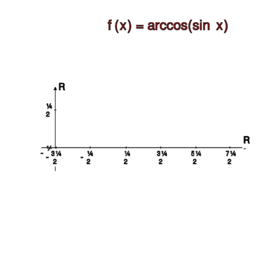
<math> y\mapsto \arccos y-\frac{\pi}{2}</math> dla <math> x\in [-\pi, 0]</math>, | <math> y\mapsto \arccos y-\frac{\pi}{2}</math> dla <math> x\in [-\pi, 0]</math>, | ||
otrzymamy <math> \arccos(\sin x)=\pi-\bigg|x+\frac{\pi}{2}\bigg| | otrzymamy <math> \arccos(\sin x)=\pi-\bigg|x+\frac{\pi}{2}\bigg|</math>. Stąd | ||
ostatecznie dla <math> x\in[-\pi, \pi]</math> mamy | ostatecznie dla <math> x\in[-\pi, \pi]</math> mamy | ||
| Linia 227: | Linia 227: | ||
zachodzą równości:<br> | zachodzą równości:<br> | ||
a) <math> \cosh(x+y)=\cosh x \cosh y+\sinh x\sinh y,</math><br> | a) <math> \cosh(x+y)=\cosh x \cosh y+\sinh x\sinh y,</math><br> | ||
b) <math> \sinh(x+y)=\sinh x\cosh y+\cosh x \sinh y | b) <math> \sinh(x+y)=\sinh x\cosh y+\cosh x \sinh y</math>. | ||
}}</span> | }}</span> | ||
| Linia 250: | Linia 250: | ||
</math></center> | </math></center> | ||
stąd <math> \cosh x \cosh y+\sinh x\sinh y=\cosh(x+y) | stąd <math> \cosh x \cosh y+\sinh x\sinh y=\cosh(x+y)</math>. | ||
b) Dokonując podobnych przekształceń jak w punkcie a), otrzymujemy: | b) Dokonując podobnych przekształceń jak w punkcie a), otrzymujemy: | ||
| Linia 263: | Linia 263: | ||
</math></center> | </math></center> | ||
stąd <math> \sinh x \cosh y+\cosh x\sinh y=\sinh(x+y) | stąd <math> \sinh x \cosh y+\cosh x\sinh y=\sinh(x+y)</math>. | ||
</div></div> | </div></div> | ||
<span id="cwiczenie_2_5">{{cwiczenie|2.5.|| | <span id="cwiczenie_2_5">{{cwiczenie|2.5.|| | ||
a) Niech <math> T_n(x):=\cos(n\arccos x)</math> dla <math> n=0,1,2, | a) Niech <math> T_n(x):=\cos(n\arccos x)</math> dla <math> n=0,1,2,..</math>.. | ||
Wykaż, że <math> T_0(x)=1</math>, <math> T_1(x)=x</math> oraz | Wykaż, że <math> T_0(x)=1</math>, <math> T_1(x)=x</math> oraz | ||
| Linia 276: | Linia 276: | ||
dla <math> n\geq 0</math>.<br> | dla <math> n\geq 0</math>.<br> | ||
b) Wykazać, że funkcja <math> T_n(x)=\cos(n\arccos x)</math> jest wielomianem | b) Wykazać, że funkcja <math> T_n(x)=\cos(n\arccos x)</math> jest wielomianem | ||
zmiennej <math> x</math>, dla <math> n=0,1,2,3, | zmiennej <math> x</math>, dla <math> n=0,1,2,3,..</math>.. | ||
}}</span> | }}</span> | ||
| Linia 308: | Linia 308: | ||
gdyż <math> \cos y=\cos(\arccos x)=x</math> oraz | gdyż <math> \cos y=\cos(\arccos x)=x</math> oraz | ||
<math> \cos ny=\cos(n\arccos x)=T_n(x) | <math> \cos ny=\cos(n\arccos x)=T_n(x)</math>. Przekształćmy także | ||
<center><math> \begin{align} | <center><math> \begin{align} | ||
| Linia 329: | Linia 329: | ||
b) Formuła wykazana w punkcie b) pozwala wyznaczyć <math> T_{n+2}</math> dla | b) Formuła wykazana w punkcie b) pozwala wyznaczyć <math> T_{n+2}</math> dla | ||
<math> n=0,1,2, | <math> n=0,1,2,..</math>.. Iloczyn i suma wielomianów jest wielomianem. | ||
Funkcje <math> T_0(x)=1</math> oraz <math> T_1(x)=x</math> są wielomianami zmiennej <math> x</math>, | Funkcje <math> T_0(x)=1</math> oraz <math> T_1(x)=x</math> są wielomianami zmiennej <math> x</math>, | ||
więc każda kolejna funkcja | więc każda kolejna funkcja | ||
| Linia 344: | Linia 344: | ||
a) Niech <math> U_n(x):=\cosh(n {\rm arcosh\, } x)</math> dla | a) Niech <math> U_n(x):=\cosh(n {\rm arcosh\, } x)</math> dla | ||
<math> n=0,1,2, | <math> n=0,1,2,..</math>.. Wykaż, że <math> U_0(x)=1</math>, <math> U_1(x)=x</math> oraz | ||
<math> U_{n+2}(x) =2xU_{n+1}(x)-U_{n}(x),\quad | <math> U_{n+2}(x) =2xU_{n+1}(x)-U_{n}(x),\quad | ||
| Linia 350: | Linia 350: | ||
b) Wykazać, że funkcja <math> U_n(x)=\cosh(n {\rm arcosh\, } x)</math> jest wielomianem | b) Wykazać, że funkcja <math> U_n(x)=\cosh(n {\rm arcosh\, } x)</math> jest wielomianem | ||
zmiennej <math> x</math>, dla <math> n=0,1,2,3, | zmiennej <math> x</math>, dla <math> n=0,1,2,3,..</math>..<br> | ||
c) Wykazać, że dla dowolnej liczby <math> n=0,1,2,3, | c) Wykazać, że dla dowolnej liczby <math> n=0,1,2,3,..</math>. istnieje | ||
wielomian <math> W_n</math> taki, że <math> U_n</math> oraz <math> T_n</math> są restrykcjami - | wielomian <math> W_n</math> taki, że <math> U_n</math> oraz <math> T_n</math> są restrykcjami - | ||
odpowiednio do przedziałów <math> [1, \infty)</math> oraz <math> [-1, 1]</math> - | odpowiednio do przedziałów <math> [1, \infty)</math> oraz <math> [-1, 1]</math> - | ||
| Linia 381: | Linia 381: | ||
gdyż <math> \cosh y=\cosh({\rm arcosh\, } x)=x</math> oraz | gdyż <math> \cosh y=\cosh({\rm arcosh\, } x)=x</math> oraz | ||
<math> \cosh(ny)=\cosh(n{\rm arcosh\, } x)=U_n(x) | <math> \cosh(ny)=\cosh(n{\rm arcosh\, } x)=U_n(x)</math>. Przekształćmy także | ||
<center><math> \begin{align} | <center><math> \begin{align} | ||
| Linia 401: | Linia 401: | ||
b) Zauważmy, że formuła wykazana w punkcie b) pozwala wyznaczyć | b) Zauważmy, że formuła wykazana w punkcie b) pozwala wyznaczyć | ||
<math> U_{n+2}</math> dla <math> n=0,1,2, | <math> U_{n+2}</math> dla <math> n=0,1,2,..</math>.. Iloczyn i suma wielomianów jest | ||
wielomianem. Ponadto funkcje <math> U_0(x)=1</math> oraz <math> U_1(x)=x</math> są | wielomianem. Ponadto funkcje <math> U_0(x)=1</math> oraz <math> U_1(x)=x</math> są | ||
wielomianami zmiennej <math> x</math>, więc każda kolejna funkcja | wielomianami zmiennej <math> x</math>, więc każda kolejna funkcja | ||
| Linia 424: | Linia 424: | ||
Wielomiany <math> T_n</math> oraz <math> U_n</math> są więc zacieśnieniem -- odpowiednio do przedziałów | Wielomiany <math> T_n</math> oraz <math> U_n</math> są więc zacieśnieniem -- odpowiednio do przedziałów | ||
<math> [-1,1]</math> oraz <math> [1,\infty)</math> - tego samego wielomianu <br> <math> W_n</math>, <math> n=0,1,2, | <math> [-1,1]</math> oraz <math> [1,\infty)</math> - tego samego wielomianu <br> <math> W_n</math>, <math> n=0,1,2,..</math>.. | ||
Zwróćmy uwagę na fakt, że dziedziną każdej z funkcji | Zwróćmy uwagę na fakt, że dziedziną każdej z funkcji | ||
<math> T_n(x)=\cos(n\arccos x)</math> jest przedział <math> [-1,1]</math> a dziedziną | <math> T_n(x)=\cos(n\arccos x)</math> jest przedział <math> [-1,1]</math> a dziedziną | ||
Wersja z 09:17, 5 wrz 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a)
b) .
Ćwiczenie 2.5.
a) Niech dla .. Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ..
Ćwiczenie 2.6.
a) Niech dla .. Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ..
c) Wykazać, że dla dowolnej liczby . istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .