PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „\displaystyle ” na „” |
m Zastępowanie tekstu – „\displaystyle” na „” |
||
| Linia 111: | Linia 111: | ||
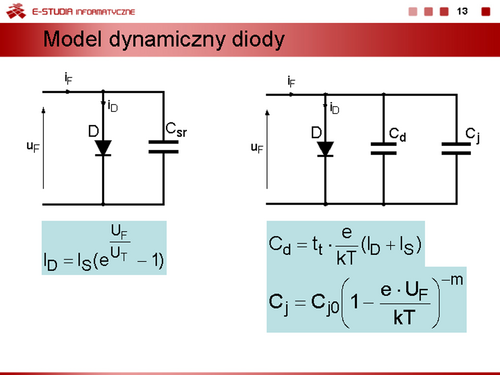
|valign="top"|Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności: | |valign="top"|Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności: | ||
<math>I_F=I_S (e^{ | <math>I_F=I_S (e^{\frac{U_F}{n\cdot U_T}}-1)</math> | ||
gdzie: | gdzie: | ||
| Linia 137: | Linia 137: | ||
|valign="top"|W ogólnym wypadku prąd nasycenia <math>I_S\,</math> zależy od temperatury złącza zgodnie z zależnością | |valign="top"|W ogólnym wypadku prąd nasycenia <math>I_S\,</math> zależy od temperatury złącza zgodnie z zależnością | ||
<math>I_S=C\cdot T^3 \cdot e^{ | <math>I_S=C\cdot T^3 \cdot e^{\frac{-E_{G0}}{U_T}}</math> | ||
gdzie: <math>C\,</math> - stała, <math>E_{G0}\,</math> - jest ekstrapolowaną (dla <math>\diplaystyle T = 0\, K</math>) szerokością przerwy energetycznej (<math>1,19\, V\,</math> dla krzemu, <math>0,78\, V\,</math> dla germanu, <math>1,56\, V\,</math> dla arsenku galu). | gdzie: <math>C\,</math> - stała, <math>E_{G0}\,</math> - jest ekstrapolowaną (dla <math>\diplaystyle T = 0\, K</math>) szerokością przerwy energetycznej (<math>1,19\, V\,</math> dla krzemu, <math>0,78\, V\,</math> dla germanu, <math>1,56\, V\,</math> dla arsenku galu). | ||
| Linia 143: | Linia 143: | ||
Ze względu na stałą <math>C\,</math> w modelach stosowanych w programach komputerowych zależność ta jest unormowana | Ze względu na stałą <math>C\,</math> w modelach stosowanych w programach komputerowych zależność ta jest unormowana | ||
<math>I_S(T)=I_S(T_0)\cdot \left(\frac{T}{T_0}\right)^3 \cdot e^{ | <math>I_S(T)=I_S(T_0)\cdot \left(\frac{T}{T_0}\right)^3 \cdot e^{\left[\frac{E_{G0}}{U_T(T_0)}\left(1-\frac{T_0}{T} \right)\right]}</math> | ||
|} | |} | ||
Wersja z 10:20, 28 sie 2023
 |
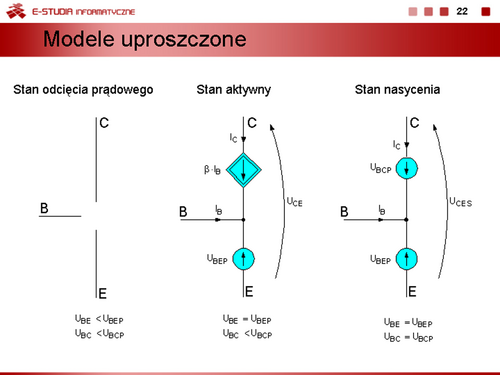
Modele elementów półprzewodnikowych |
 |
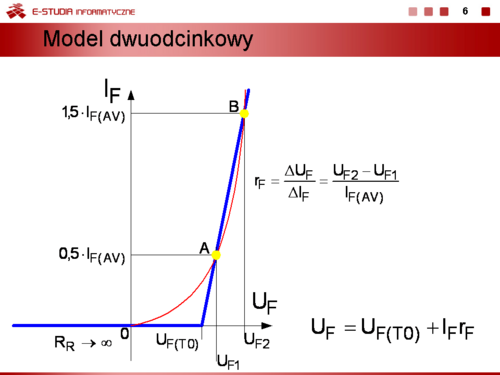
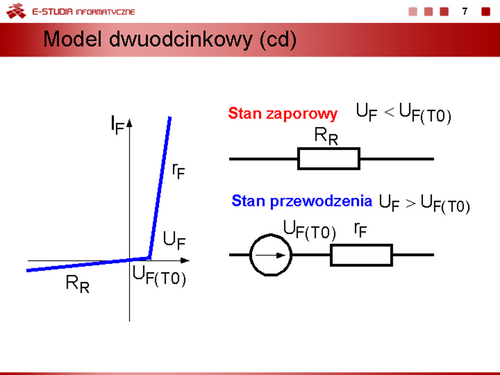
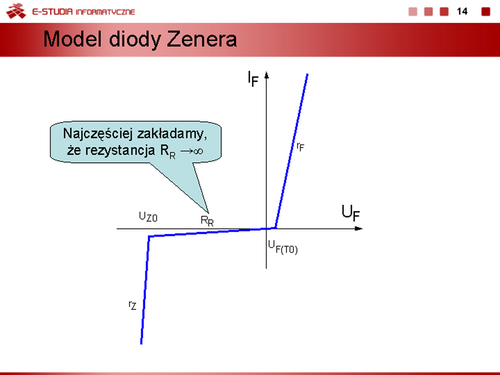
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. |
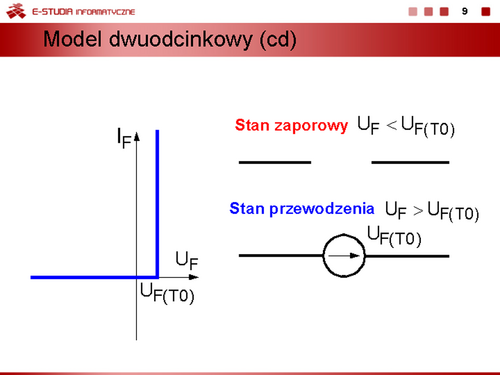 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
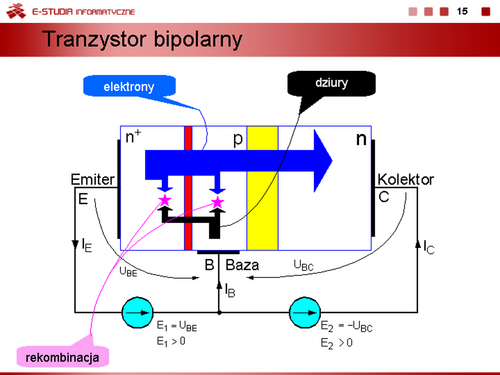
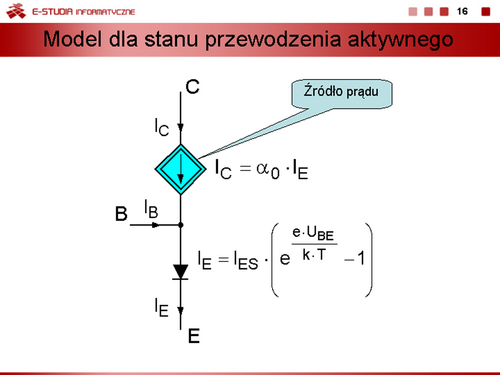
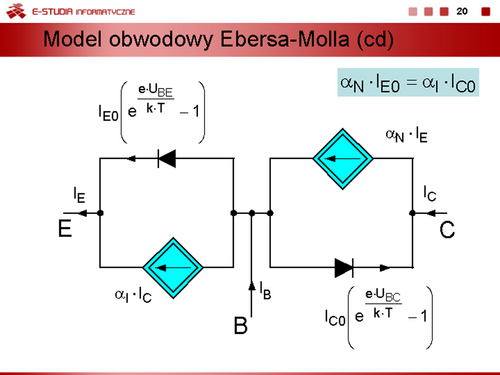
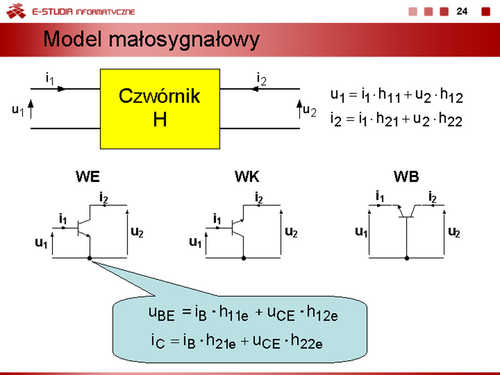
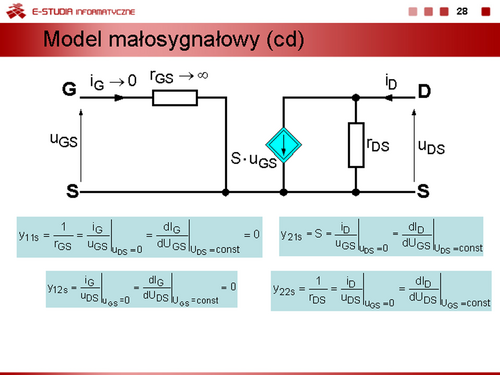
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
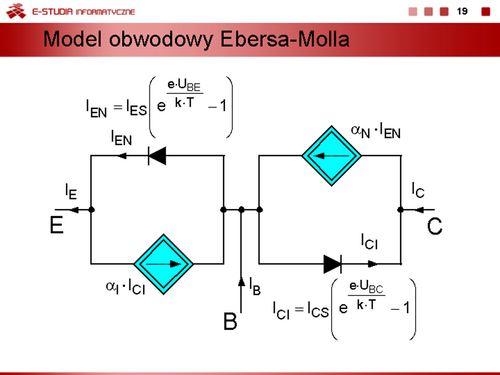 |
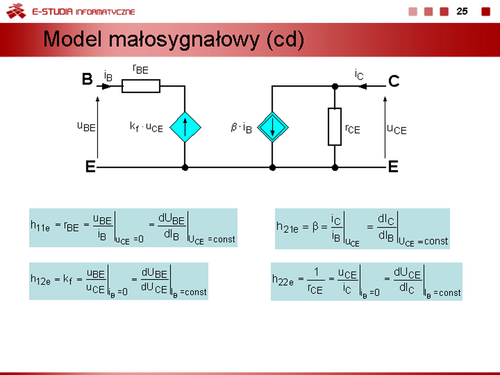
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976