Analiza matematyczna 2/Ćwiczenia 12: Całka krzwoliniowa. Twierdzenie Greena: Różnice pomiędzy wersjami
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*)px;"> <flashwrap>file=(.*).swf\|size=small<\/flashwrap> <div\.thumbcaption>(.*)<\/div><\/div> <\/div>" na "$2x$2px|thumb|$1|$4" |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 5: | Linia 5: | ||
Policzyć | Policzyć | ||
<center><math> | <center><math>\displaystyle\int\limits_C ydx+2x dy, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>C</math> jest łukiem cykloidy danej | ||
parametrycznie: | parametrycznie: | ||
<center><math> | <center><math>x=t-\sin t, \ y=1-\cos t, \ t\in [0, 2\pi]. | ||
</math></center> | </math></center> | ||
| Linia 28: | Linia 28: | ||
<center> | <center> | ||
<math> | <math>\begin{align} \displaystyle\int\limits_C ydx+2x dy | ||
&= | &= | ||
\displaystyle\int\limits_0^{2\pi}(1-\cos t)(t-\sin t)'+2(t-\sin | \displaystyle\int\limits_0^{2\pi}(1-\cos t)(t-\sin t)'+2(t-\sin | ||
| Linia 50: | Linia 50: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_K (x+y)dx+y^2 dy, | ||
</math> | </math> | ||
</center> | </center> | ||
gdzie <math> | gdzie <math>K</math> jest kwadratem o wierzchołkach | ||
w <math> | w <math>(-1,-1), (1,-1), (1,1), (-1,1)</math> obieganym przeciwnie do ruchu | ||
wskazówek zegara. | wskazówek zegara. | ||
}} | }} | ||
| Linia 64: | Linia 64: | ||
skorzystanie z definicji. Drugi sposób, to zastosowanie | skorzystanie z definicji. Drugi sposób, to zastosowanie | ||
twierdzenia Greena - nasza krzywa jest krzywą zamkniętą i | twierdzenia Greena - nasza krzywa jest krzywą zamkniętą i | ||
zorientowaną dodatnio, funkcje <math> | zorientowaną dodatnio, funkcje <math>P(x,y)=x+y</math> i <math>Q(x, y)=y^2</math> są | ||
ciągłe i mają ciągłe pochodne cząstkowe, więc twierdzenie Greena | ciągłe i mają ciągłe pochodne cząstkowe, więc twierdzenie Greena | ||
można stosować. | można stosować. | ||
| Linia 72: | Linia 72: | ||
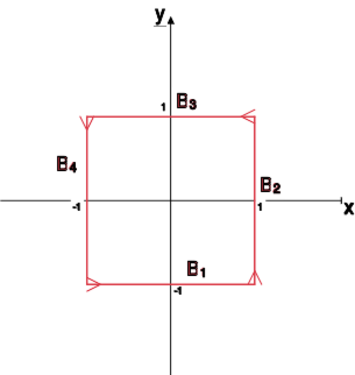
'''Sposób I''': Oznaczmy boki kwadratu. Niech<br> | '''Sposób I''': Oznaczmy boki kwadratu. Niech<br> | ||
<math> | <math>B_1</math> będzie odcinkiem łączącym <math>(-1,-1)</math> z <math>(1,-1)</math>;<br> | ||
<math> | <math>B_2</math> będzie odcinkiem łączącym <math>(1,-1)</math> z <math>(1,1)</math>;<br> | ||
<math> | <math>B_3</math> będzie odcinkiem łączącym <math>(1,1)</math> z <math>(-1,1)</math>;<br> | ||
<math> | <math>B_4</math> będzie odcinkiem łączącym <math>(-1,1)</math> z <math>(-1,-1).</math> | ||
[[File:Am2.12.5.svg|375x375px|thumb|left|Orientacja krzywej z ćwiczenia 12.2.]] | [[File:Am2.12.5.svg|375x375px|thumb|left|Orientacja krzywej z ćwiczenia 12.2.]] | ||
Zwróćmy uwagę na to, że musimy tak dobrać parametryzację | Zwróćmy uwagę na to, że musimy tak dobrać parametryzację | ||
odcinków <math> | odcinków <math>B_1,\ldots,B_4,</math> by ta parametryzacja dawała orientację | ||
zgodną z orientacją <math> | zgodną z orientacją <math>K</math> zobacz rysunek.<br> | ||
Wypiszmy zatem parametryzacje tych odcinków. Dla <math> | Wypiszmy zatem parametryzacje tych odcinków. Dla <math>B_1,\ldots,B_4</math> | ||
mamy odpowiednio: | mamy odpowiednio: | ||
<center> | <center> | ||
<math> | <math>\begin{align} | ||
\gamma_1(t) &= (t,-1), t\in[-1,1],\\ | \gamma_1(t) &= (t,-1), t\in[-1,1],\\ | ||
\gamma_2(t) &= (1,t), t\in[-1,1],\\ | \gamma_2(t) &= (1,t), t\in[-1,1],\\ | ||
| Linia 96: | Linia 96: | ||
<center> | <center> | ||
<math> | <math>\begin{align} & | ||
\displaystyle\int\limits_K (x+y)dx+y^2 dy\\ | \displaystyle\int\limits_K (x+y)dx+y^2 dy\\ | ||
&= | &= | ||
| Linia 113: | Linia 113: | ||
'''Sposób II.''' | '''Sposób II.''' | ||
Skorzystajmy z twierdzenia Greena. Oznaczmy przez <math> | Skorzystajmy z twierdzenia Greena. Oznaczmy przez <math>D</math> | ||
wnętrze kwadratu ograniczonego krzywą <math> | wnętrze kwadratu ograniczonego krzywą <math>K.</math> | ||
Policzmy najpierw | Policzmy najpierw | ||
<center><math> | <center><math>\frac{\partial Q}{\partial x} -\frac{\partial P}{\partial y} | ||
= | = | ||
\frac{\partial (y^2)}{\partial x}-\frac{\partial | \frac{\partial (y^2)}{\partial x}-\frac{\partial | ||
| Linia 127: | Linia 127: | ||
Dostajemy zatem: | Dostajemy zatem: | ||
<center><math> | <center><math>\displaystyle\int\limits_K (x+y)dx+y^2 dy | ||
= | = | ||
\iint\limits_D-1 dxdy | \iint\limits_D-1 dxdy | ||
= | = | ||
- </math> (pole kwadratu o boku <math> | - </math> (pole kwadratu o boku <math>2</math>) <math> | ||
= | = | ||
-4. | -4. | ||
| Linia 142: | Linia 142: | ||
W pewnym polu sił składowe pola wynoszą | W pewnym polu sił składowe pola wynoszą | ||
<center><math> | <center><math>P(x,y) | ||
= | = | ||
3x^2y+2xy^2+1, \quad | 3x^2y+2xy^2+1, \quad | ||
| Linia 151: | Linia 151: | ||
Policzyć pracę | Policzyć pracę | ||
potrzebną do przesunięcia punktu materialnego wzdłuż krzywej <math> | potrzebną do przesunięcia punktu materialnego wzdłuż krzywej <math>K</math> | ||
łączącej punkt <math> | łączącej punkt <math>(0,0)</math> z punktem <math>(1,1),</math> danej wzorem <math>y=x^{20}.</math> | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Zadanie można zrobić na dwa sposoby. Pierwszy sposób to | Zadanie można zrobić na dwa sposoby. Pierwszy sposób to | ||
sparametryzowanie krzywej: <math> | sparametryzowanie krzywej: <math>x=t, y=t^{20}, t\in[0,1]</math> i wstawienie | ||
do wzoru. Inny pomysł to zauważenie, że dane pole sił jest polem | do wzoru. Inny pomysł to zauważenie, że dane pole sił jest polem | ||
potencjalnym, zatem obliczana praca nie zależy od drogi. Można | potencjalnym, zatem obliczana praca nie zależy od drogi. Można | ||
więc wybrać dowolną drogę całkowania, najlepiej odcinek łączący | więc wybrać dowolną drogę całkowania, najlepiej odcinek łączący | ||
punkt <math> | punkt <math>(0,0)</math> z punktem <math>(1,1).</math> | ||
</div></div> | </div></div> | ||
| Linia 167: | Linia 167: | ||
'''Sposób I.''' | '''Sposób I.''' | ||
Parametryzujemy daną krzywą: | Parametryzujemy daną krzywą: | ||
<math> | <math>x=t, y=t^{20}, t\in[0,1]</math> i wstawiamy do wzoru na pracę | ||
<center><math> | <center><math>\begin{align} | ||
W | W | ||
&= | &= | ||
| Linia 184: | Linia 184: | ||
'''Sposób II.''' | '''Sposób II.''' | ||
Zauważmy, że dane pole jest potencjalne w <math> | Zauważmy, że dane pole jest potencjalne w <math>\displaystyle\mathbb{R}^2,</math> bo | ||
<center><math> | <center><math>\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial | ||
y} | y} | ||
= | = | ||
| Linia 193: | Linia 193: | ||
a zatem całka nie zależy od drogi całkowania. | a zatem całka nie zależy od drogi całkowania. | ||
Zamiast krzywej <math> | Zamiast krzywej <math>K</math> możemy wziąć zatem odcinek <math>T</math> łączący | ||
punkt <math> | punkt <math>(0,0)</math> z punktem <math>(1,1)</math> sparametryzowany następująco: | ||
<center><math> | <center><math>x=t, | ||
y=t, | y=t, | ||
t\in[0,1]. | t\in[0,1]. | ||
| Linia 203: | Linia 203: | ||
Licząc pracę, dostajemy: | Licząc pracę, dostajemy: | ||
<center><math> | <center><math>\begin{align} | ||
W | W | ||
&= | &= | ||
| Linia 224: | Linia 224: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Jak wiemy z wykładu, | Jak wiemy z wykładu, | ||
potencjał pola to taka funkcja <math> | potencjał pola to taka funkcja <math>\displaystyle\varrho,</math> że | ||
<center><math> | <center><math>(P(x,y),Q(x,y)) | ||
= | = | ||
\left(\frac{\partial \varrho}{\partial x}(x,y), | \left(\frac{\partial \varrho}{\partial x}(x,y), | ||
| Linia 236: | Linia 236: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Szukamy funkcji <math> | Szukamy funkcji <math>\displaystyle\varrho :\mathbb{R}^2\to \mathbb{R}</math> takiej, że | ||
<center><math> | <center><math>3x^2y+2xy^2+1 | ||
= | = | ||
\frac{\partial \varrho}{\partial x}(x,y) | \frac{\partial \varrho}{\partial x}(x,y) | ||
| Linia 245: | Linia 245: | ||
i | i | ||
<center><math> | <center><math>x^3+2x^2y+1 | ||
= | = | ||
\frac{\partial \varrho}{\partial y}(x,y). | \frac{\partial \varrho}{\partial y}(x,y). | ||
| Linia 251: | Linia 251: | ||
Policzmy | Policzmy | ||
całkę po <math> | całkę po <math>x</math> z obu stron pierwszej równości | ||
<center><math> | <center><math>\int \big(3x^2y+2xy^2+1\big)dx | ||
= | = | ||
\int \frac{\partial \varrho}{\partial x}(x,y)dx, | \int \frac{\partial \varrho}{\partial x}(x,y)dx, | ||
| Linia 260: | Linia 260: | ||
dostaniemy | dostaniemy | ||
<center><math> | <center><math>\varrho(x,y) | ||
= | = | ||
x^3y+x^2y^2+x+g(y), | x^3y+x^2y^2+x+g(y), | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>g</math> jest pewną | ||
różniczkowalną funkcją zmiennej <math> | różniczkowalną funkcją zmiennej <math>y.</math> (Dla sprawdzenia można | ||
policzyć pochodną po <math> | policzyć pochodną po <math>x</math> z obu stron tej równości). Aby znaleźć | ||
<math> | <math>g</math>, policzmy pochodną po <math>y</math> | ||
<center><math> | <center><math>\frac{\partial \varrho(x,y)}{\partial y} | ||
= | = | ||
\frac{\partial(x^3y+x^2y^2+y+g(y))}{\partial y} | \frac{\partial(x^3y+x^2y^2+y+g(y))}{\partial y} | ||
| Linia 279: | Linia 279: | ||
a skoro mamy mieć | a skoro mamy mieć | ||
<center><math> | <center><math>x^3+2x^2y+1 | ||
= | = | ||
\frac{\partial \varrho}{\partial y}(x,y), | \frac{\partial \varrho}{\partial y}(x,y), | ||
| Linia 286: | Linia 286: | ||
to musi być | to musi być | ||
<center><math> | <center><math>g'(y) | ||
= | = | ||
0, | 0, | ||
| Linia 293: | Linia 293: | ||
czyli | czyli | ||
<center><math> | <center><math>g(y) | ||
= | = | ||
</math> const. </center> | </math> const. </center> | ||
| Linia 300: | Linia 300: | ||
przykład: | przykład: | ||
<center><math> | <center><math>\varrho(x,y) | ||
= | = | ||
x^3y+x^2y^2+y+x | x^3y+x^2y^2+y+x | ||
</math></center> | </math></center> | ||
(wzięliśmy <math> | (wzięliśmy <math>g(y)\equiv 0</math>). | ||
Zauważmy, że policzona w poprzednim zadaniu całka | Zauważmy, że policzona w poprzednim zadaniu całka | ||
<center><math> | <center><math>\displaystyle\int\limits_T(3x^2y+2xy^2+1)dx+(x^3+2x^2y+1)dy | ||
= | = | ||
4 | 4 | ||
| Linia 325: | Linia 325: | ||
Korzystając z twierdzenia Greena, policzyć | Korzystając z twierdzenia Greena, policzyć | ||
<center><math> | <center><math>\displaystyle\int\limits_K -yx^2dx+xy^2dy, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>K</math> jest okręgiem | ||
środku w <math> | środku w <math>(0,0)</math> i promieniu <math>1.</math> | ||
}} | }} | ||
| Linia 339: | Linia 339: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Korzystamy z | Korzystamy z | ||
twierdzenia Greena. Niech <math> | twierdzenia Greena. Niech <math>D</math> oznacza koło o promieniu <math>1:</math> | ||
<center><math> | <center><math>\begin{align} | ||
\displaystyle\int\limits_K -yx^2dx+xy^2dy | \displaystyle\int\limits_K -yx^2dx+xy^2dy | ||
&= | &= | ||
| Linia 359: | Linia 359: | ||
Policzyć całkę | Policzyć całkę | ||
<center><math> | <center><math>\displaystyle\int\limits_K(e^x+e^y-y )dx+(xe^y)dy, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>K</math> jest wykresem funkcji | ||
<math> | <math>y=\sin x,</math> dla <math>x\in [0,\pi].</math> | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Krzywa <math> | Krzywa <math>K</math> nie jest krzywą zamkniętą, można jednak | ||
"dokleić" do niej odcinek <math> | "dokleić" do niej odcinek <math>[0,\pi]</math> - wtedy krzywa będzie | ||
ograniczać pewien obszar <math> | ograniczać pewien obszar <math>D.</math> Teraz można skorzystać z | ||
twierdzenia Greena. | twierdzenia Greena. | ||
</div></div> | </div></div> | ||
| Linia 375: | Linia 375: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
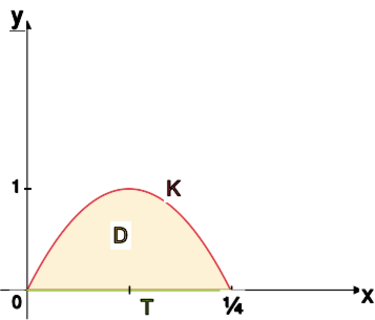
[[File:Am2.12.6.svg|375x375px|thumb|left|Obszar <math>D</math> ograniczony wykresem funkcji <math>\sin</math> oraz osią <math>Ox</math>]] | [[File:Am2.12.6.svg|375x375px|thumb|left|Obszar <math>D</math> ograniczony wykresem funkcji <math>\sin</math> oraz osią <math>Ox</math>]] | ||
Krzywą <math> | Krzywą <math>K</math> oczywiście możemy | ||
sparametryzować <math> | sparametryzować <math>x=t, y=\sin t, t\in [0,\pi].</math> Licząc całkę, | ||
dostajemy: | dostajemy: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_K(e^x+e^y-y )dx+(xe^y)dy | ||
= | = | ||
\displaystyle\int\limits_0^{\pi}(e^t+e^{\sin t} - \sin | \displaystyle\int\limits_0^{\pi}(e^t+e^{\sin t} - \sin | ||
| Linia 387: | Linia 387: | ||
</center> | </center> | ||
Znalezienie pierwotnej z <math> | Znalezienie pierwotnej z <math>e^{\sin t}</math> | ||
albo z <math> | albo z <math>te^{\sin t}\cos t</math> przekracza nasze możliwości. | ||
Spróbujmy zatem wykorzystać twierdzenie Greena. Skoro krzywa <math> | Spróbujmy zatem wykorzystać twierdzenie Greena. Skoro krzywa <math>K</math> | ||
nie jest zamknięta, musimy najpierw "dokleić" do niej inną krzywą, | nie jest zamknięta, musimy najpierw "dokleić" do niej inną krzywą, | ||
tak by razem ograniczały jakiś obszar. Weźmy zatem jako tą | tak by razem ograniczały jakiś obszar. Weźmy zatem jako tą | ||
dodatkową krzywą odcinek <math> | dodatkową krzywą odcinek <math>T:=[0, \pi].</math> Obszar ograniczony | ||
odcinkiem i wykresem funkcji <math> | odcinkiem i wykresem funkcji <math>\displaystyle\sin x</math> nazwiemy | ||
<math> | <math>D.</math><br> | ||
Aby zastosować | Aby zastosować | ||
do tego obszaru twierdzenie Greena, musimy mieć <math> | do tego obszaru twierdzenie Greena, musimy mieć <math>\displaystyle\partial D</math> | ||
zorientowany dodatnio, a zatem krzywą <math> | zorientowany dodatnio, a zatem krzywą <math>K</math> będziemy teraz | ||
przebiegać w kierunku od <math> | przebiegać w kierunku od <math>x=\pi</math> do <math>x=0,</math> przeciwnym do zadanego. | ||
Brzeg <math> | Brzeg <math>D</math> możemy więc zapisać jako <math>\displaystyle\partial D=-K+T.</math> Mamy zatem: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_{\partial D}(e^x+e^y-y )dx+(xe^y)dy | ||
= | = | ||
\displaystyle\int\limits_{-K}(e^x+e^y-y)dx+(xe^y)dy+\displaystyle\int\limits_T(e^x+e^y-y )dx+(xe^y)dy. | \displaystyle\int\limits_{-K}(e^x+e^y-y)dx+(xe^y)dy+\displaystyle\int\limits_T(e^x+e^y-y )dx+(xe^y)dy. | ||
| Linia 413: | Linia 413: | ||
<center> | <center> | ||
<math> | <math>\begin{align} \displaystyle\int\limits_{\partial D}(e^x+e^y-y)dx+(xe^y)dy | ||
&= | &= | ||
\iint\limits_D\left(\frac{\partial (xe^y)}{\partial x}-\frac{\partial (e^x+e^y-y )}{\partial | \iint\limits_D\left(\frac{\partial (xe^y)}{\partial x}-\frac{\partial (e^x+e^y-y )}{\partial | ||
| Linia 430: | Linia 430: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_T(e^x+e^y-y )dx+(xe^y)dy. | ||
</math> | </math> | ||
</center> | </center> | ||
Parametryzując <math> | Parametryzując <math>T</math> jako <math>x=t, y=0, t\in [0, \pi]</math>, mamy: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_T(e^x+e^y-y )dx+(xe^y)dy | ||
= | = | ||
\displaystyle\int\limits_0^{\pi}e^t+1dt | \displaystyle\int\limits_0^{\pi}e^t+1dt | ||
| Linia 448: | Linia 448: | ||
<center> | <center> | ||
<math> | <math>2 | ||
= | = | ||
\displaystyle\int\limits_{\partial D}(e^x+e^y-y )dx+(xe^y)dy | \displaystyle\int\limits_{\partial D}(e^x+e^y-y )dx+(xe^y)dy | ||
| Linia 458: | Linia 458: | ||
A zatem | A zatem | ||
<center><math> | <center><math>\displaystyle\int\limits_{K}(e^x+e^y-y )dx+(xe^y)dy | ||
= | = | ||
-\displaystyle\int\limits_{-K}(e^x+e^y-y)dx+(xe^y)dy=e^{\pi}+\pi-3. | -\displaystyle\int\limits_{-K}(e^x+e^y-y)dx+(xe^y)dy=e^{\pi}+\pi-3. | ||
| Linia 469: | Linia 469: | ||
Policzyć całkę krzywoliniową: | Policzyć całkę krzywoliniową: | ||
<center><math> | <center><math>\displaystyle\int\limits_K (e^{x}\sin y)dx+(e^{x}\cos y)dy, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>K</math> jest parabolą | ||
<math> | <math>y=-x^2+1</math> pomiędzy punktami <math>(-1,0)</math> a <math>(1,0).</math> | ||
}} | }} | ||
| Linia 486: | Linia 486: | ||
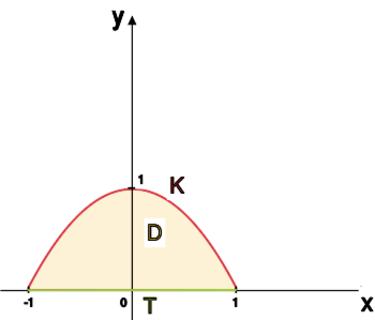
przy pomocy sparametryzowania krzywej będzie trudne. Postaramy sie | przy pomocy sparametryzowania krzywej będzie trudne. Postaramy sie | ||
skorzystać z twierdzenia Greena. Aby dostać krzywą zamkniętą, do | skorzystać z twierdzenia Greena. Aby dostać krzywą zamkniętą, do | ||
krzywej <math> | krzywej <math>K</math> "doklejamy" odcinek <math>T=[-1,1].</math> Otrzymany obszar | ||
oznaczamy przez <math> | oznaczamy przez <math>D.</math><br> | ||
Brzeg <math> | Brzeg <math>D</math> ma być zorientowany dodatnio, zatem na krzywej <math>K</math> | ||
musimy wziąć parametryzację dającą orientację przeciwną, | musimy wziąć parametryzację dającą orientację przeciwną, | ||
<math> | <math>\displaystyle\partial D=-K+T.</math> Mamy zatem: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_{\partial D} (e^{x}\sin y)dx+(e^{x}\cos y)dy | ||
= | = | ||
\iint\limits_D\frac{\partial(e^{x}\cos y)}{\partial x}-\frac{\partial(e^{x}\sin y)}{\partial y}\ dxdy | \iint\limits_D\frac{\partial(e^{x}\cos y)}{\partial x}-\frac{\partial(e^{x}\sin y)}{\partial y}\ dxdy | ||
| Linia 507: | Linia 507: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_{\partial D} (e^{x}\sin y)dx+(e^{x}\cos y)dy | ||
= | = | ||
\displaystyle\int\limits_K (e^{x}\sin y)dx+(e^{x}\cos y)dy+\displaystyle\int\limits_{T} (e^{x}\sin | \displaystyle\int\limits_K (e^{x}\sin y)dx+(e^{x}\cos y)dy+\displaystyle\int\limits_{T} (e^{x}\sin | ||
| Linia 514: | Linia 514: | ||
</center> | </center> | ||
Biorąc parametryzację odcinka <math> | Biorąc parametryzację odcinka <math>T</math>: <math>x=t, y=0, t\in[-1,1]</math>, | ||
dostajemy od razu | dostajemy od razu | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_{T} (e^{x}\sin y)dx+(e^{x}\cos y)dy | ||
= | = | ||
\displaystyle\int\limits_{-1}^1 | \displaystyle\int\limits_{-1}^1 | ||
| Linia 530: | Linia 530: | ||
<center> | <center> | ||
<math> | <math>\displaystyle\int\limits_K (e^{x}\sin y)dx-(e^{x}\cos y)dy | ||
= | = | ||
0. | 0. | ||
| Linia 541: | Linia 541: | ||
Za pomocą całki krzywoliniowej skierowanej | Za pomocą całki krzywoliniowej skierowanej | ||
obliczyć pole ograniczone elipsą <math> | obliczyć pole ograniczone elipsą <math>E</math> | ||
<center> | <center> | ||
<math> | <math>\frac{x^2}{a^2}+\frac{y^2}{b^2} | ||
= | = | ||
1, | 1, | ||
| Linia 550: | Linia 550: | ||
</center> | </center> | ||
gdzie <math> | gdzie <math>a, b>0</math> są dane. | ||
}} | }} | ||
| Linia 556: | Linia 556: | ||
[[File:AM2.M12.C.R05.mp4|253x253px|thumb|right|Elipsa]] | [[File:AM2.M12.C.R05.mp4|253x253px|thumb|right|Elipsa]] | ||
Parametryzacja elipsy to <math> | Parametryzacja elipsy to <math>x=a\cos t, y=b\sin t, t\in[0,2\pi].</math><br> | ||
</div></div> | </div></div> | ||
| Linia 564: | Linia 564: | ||
<center> | <center> | ||
<math> | <math>x=a\cos t, y=b\sin t, \ t\in[0,2\pi]. | ||
</math> | </math> | ||
</center> | </center> | ||
Jak wiemy z wykładu, pole powierzchni obszaru | Jak wiemy z wykładu, pole powierzchni obszaru | ||
ograniczonego krzywą <math> | ograniczonego krzywą <math>E</math> wyraża się wzorem: | ||
<center> | <center> | ||
<math> | <math>|D| | ||
= | = | ||
\oint_E xdy. | \oint_E xdy. | ||
| Linia 581: | Linia 581: | ||
<center> | <center> | ||
<math> | <math>|D| | ||
= | = | ||
\oint_E xdy | \oint_E xdy | ||
| Linia 600: | Linia 600: | ||
Za pomocą całki krzywoliniowej | Za pomocą całki krzywoliniowej | ||
skierowanej obliczyć pole ograniczone asteroidą <math> | skierowanej obliczyć pole ograniczone asteroidą <math>A</math> | ||
<center> | <center> | ||
<math> | <math>x^{\frac{2}{3}}+y^{\frac{2}{3}} | ||
= | = | ||
a^{\frac{2}{3}}, | a^{\frac{2}{3}}, | ||
| Linia 609: | Linia 609: | ||
</center> | </center> | ||
gdzie <math> | gdzie <math>a>0</math> | ||
jest dane. | jest dane. | ||
}} | }} | ||
| Linia 617: | Linia 617: | ||
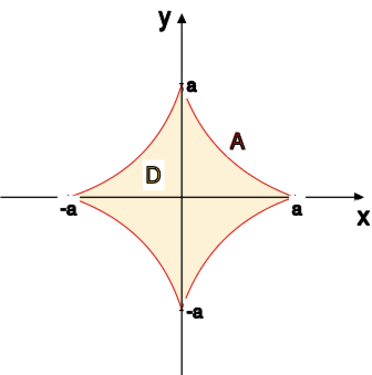
[[File:Am2.12.8.svg|375x375px|thumb|left|Asteroida]] | [[File:Am2.12.8.svg|375x375px|thumb|left|Asteroida]] | ||
Parametryzacja | Parametryzacja | ||
asteroidy to <math> | asteroidy to <math>x=a\cos^3t, y=a\sin^3t, t\in [0, 2\pi].</math><br> | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Już wiemy, że parametryzacja asteroidy | Już wiemy, że parametryzacja asteroidy | ||
to <math> | to <math>x=a\cos^3t, y=a\sin^3t, t\in [0, 2\pi],</math> zastosujmy zatem wzór | ||
na pole: | na pole: | ||
<center> | <center> | ||
<math> | <math>\begin{align} | ||
|D| | |D| | ||
&= | &= | ||
| Linia 645: | Linia 645: | ||
<center> | <center> | ||
<math> | <math>\begin{align} | ||
\int\cos^4 t dt | \int\cos^4 t dt | ||
&= | &= | ||
| Linia 658: | Linia 658: | ||
</center> | </center> | ||
(wzór na <math> | (wzór na <math>\displaystyle\int \cos^nt\,dt</math> | ||
można wyprowadzić rekurencyjnie) | można wyprowadzić rekurencyjnie) | ||
zatem dostajemy: | zatem dostajemy: | ||
<center> | <center> | ||
<math> | <math>3a^2\displaystyle\int\limits_0^{2\pi}\cos^4t-\cos^6t\ dt | ||
= | = | ||
3a^2\left(\frac{t}{16}+ \frac{1}{64} \sin 2t - \frac{1}{64} \sin | 3a^2\left(\frac{t}{16}+ \frac{1}{64} \sin 2t - \frac{1}{64} \sin | ||
Wersja z 08:47, 28 sie 2023
Całka krzywoliniowa. Twierdzenie Greena
Ćwiczenie 12.1.
Policzyć
gdzie jest łukiem cykloidy danej parametrycznie:
Ćwiczenie 12.2.
Policzyć
gdzie jest kwadratem o wierzchołkach w obieganym przeciwnie do ruchu wskazówek zegara.
Ćwiczenie 12.3.
W pewnym polu sił składowe pola wynoszą
Policzyć pracę potrzebną do przesunięcia punktu materialnego wzdłuż krzywej łączącej punkt z punktem danej wzorem
Ćwiczenie 12.4.
Znaleźć (lub odgadnąć) potencjał dla pola sił z ćwiczenia 12.3.
Ćwiczenie 12.5.
Korzystając z twierdzenia Greena, policzyć
gdzie jest okręgiem środku w i promieniu
Ćwiczenie 12.6.
Policzyć całkę
gdzie jest wykresem funkcji dla
Ćwiczenie 12.7.
Policzyć całkę krzywoliniową:
gdzie jest parabolą pomiędzy punktami a
Ćwiczenie 12.8.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone elipsą
gdzie są dane.
Ćwiczenie 12.9.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone asteroidą
gdzie jest dane.