PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 64: | Linia 64: | ||
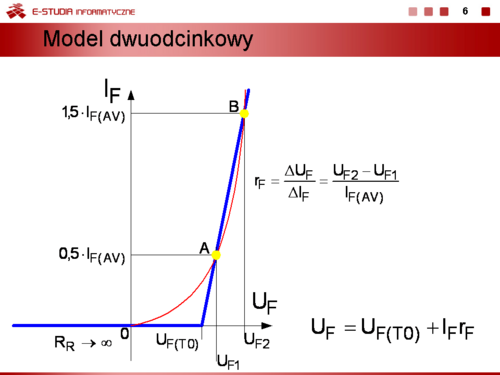
Dla tego modelu w stanie przewodzenia można napisać: | Dla tego modelu w stanie przewodzenia można napisać: | ||
<math> | <math>U_F=U_{F(T0)}+I_F r_F</math> | ||
gdzie: | gdzie: | ||
<math> | <math>U_{F(T0)}</math> - napięcie progu załączenia diody, | ||
<math> | <math>r_F\,</math> - rezystancja dynamiczna diody. | ||
Definicję rezystancji dynamicznej diody przedstawiono na slajdzie. | Definicję rezystancji dynamicznej diody przedstawiono na slajdzie. | ||
| Linia 88: | Linia 88: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd8.png|thumb|500px]] | ||
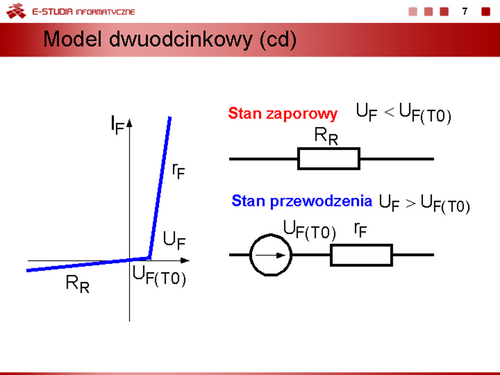
|valign="top"|Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym <math> | |valign="top"|Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym <math>R_R \to \infty</math>. W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. | ||
|} | |} | ||
| Linia 111: | Linia 111: | ||
|valign="top"|Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności: | |valign="top"|Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności: | ||
<math> | <math>I_F=I_S (e^{\displaystyle\frac{U_F}{n\cdot U_T}}-1)</math> | ||
gdzie: | gdzie: | ||
<math> | <math>I_F, U_F\,</math> – prąd i napięcie przewodzenia, | ||
<math> | <math>I_S\,</math> – prąd nasycenia płynący przy polaryzacji wstecznej złącza (prąd wsteczny), | ||
<math> | <math>n\,</math> – współczynnik emisji, | ||
<math> | <math>U_T = kT/e\,</math> - potencjał elektrokinetyczny lub potencjał termiczny elektronu (w temperaturze pokojowej około <math>25\, mV\,</math>), | ||
<math> | <math>k\,</math> - stała Boltzmana <math>1,38 \cdot 10^{-23}\, J/K</math>, | ||
<math> | <math>T\,</math> – temperatura bezwzględna, | ||
<math> | <math>e\,</math> – ładunek elementarny <math>1,6\cdot 10^{-19}\, C\,</math> | ||
|} | |} | ||
| Linia 135: | Linia 135: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd12.png|thumb|500px]] | ||
|valign="top"|W ogólnym wypadku prąd nasycenia <math> | |valign="top"|W ogólnym wypadku prąd nasycenia <math>I_S\,</math> zależy od temperatury złącza zgodnie z zależnością | ||
<math> | <math>I_S=C\cdot T^3 \cdot e^{\displaystyle\frac{-E_{G0}}{U_T}}</math> | ||
gdzie: <math> | gdzie: <math>C\,</math> - stała, <math>E_{G0}\,</math> - jest ekstrapolowaną (dla <math>\diplaystyle T = 0\, K</math>) szerokością przerwy energetycznej (<math>1,19\, V\,</math> dla krzemu, <math>0,78\, V\,</math> dla germanu, <math>1,56\, V\,</math> dla arsenku galu). | ||
Ze względu na stałą <math> | Ze względu na stałą <math>C\,</math> w modelach stosowanych w programach komputerowych zależność ta jest unormowana | ||
<math> | <math>I_S(T)=I_S(T_0)\cdot \left(\frac{T}{T_0}\right)^3 \cdot e^{\displaystyle\left[\frac{E_{G0}}{U_T(T_0)}\left(1-\frac{T_0}{T} \right)\right]}</math> | ||
|} | |} | ||
| Linia 155: | Linia 155: | ||
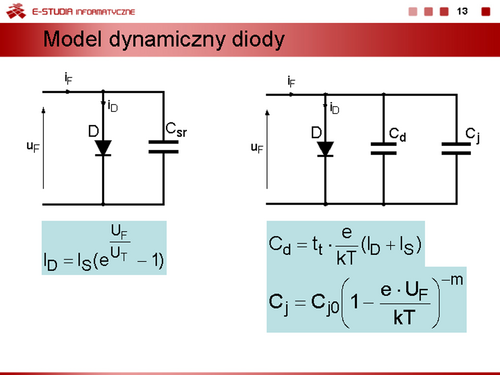
W obliczeniach komputerowych używa się dokładniejszego modelu uwzględniającego pojemność dyfuzyjną złącza <math>C_d\,</math> i pojemność warstwy zaporowej ( pojemność złączową) <math>C_j\,</math>. | W obliczeniach komputerowych używa się dokładniejszego modelu uwzględniającego pojemność dyfuzyjną złącza <math>C_d\,</math> i pojemność warstwy zaporowej ( pojemność złączową) <math>C_j\,</math>. | ||
<math> | <math>C_d=t_t \frac{e}{kT}(I_D+I_S)</math> | ||
gdzie <math>t_t\,</math> – czas przelotu. | gdzie <math>t_t\,</math> – czas przelotu. | ||
<math> | <math>C_j=C_{j0}\left(1-\frac{U_R}{U_D} \right)^{-m}=C_{j0}\left(1-\frac{e\cdot U_F}{kT} \right)^{-m}</math> , | ||
gdzie <math>C_{j0}\,</math> pojemność złącza przy zerowym napięciu polaryzacji, <math>m = 0,5\,</math> dla złącza skokowego, <math>m = 0,333\,</math> dla złącza liniowego, <math>U_R\,</math> napięcie wsteczne diody, <math>U_D\,</math> potencjał dyfuzyjny złącza. | gdzie <math>C_{j0}\,</math> pojemność złącza przy zerowym napięciu polaryzacji, <math>m = 0,5\,</math> dla złącza skokowego, <math>m = 0,333\,</math> dla złącza liniowego, <math>U_R\,</math> napięcie wsteczne diody, <math>U_D\,</math> potencjał dyfuzyjny złącza. | ||
| Linia 167: | Linia 167: | ||
Do opisu modelu bezinercyjnego stosuje się uproszczony wzór Shockleya | Do opisu modelu bezinercyjnego stosuje się uproszczony wzór Shockleya | ||
<math> | <math>I_D=I_S \bigg(e^{\frac{U_F}{U_T}}-1\bigg)</math> | ||
| Linia 178: | Linia 178: | ||
Konduktancję diody można wyznaczyć z zależności: | Konduktancję diody można wyznaczyć z zależności: | ||
<math> | <math>g_D=\frac{1}{r_D}=\frac{dI_D}{dU_F}=\frac{1}{U_T}(I_D+I_S)</math> | ||
Ponieważ w stanie przewodzenia <math>I_D >> I_S</math>. | Ponieważ w stanie przewodzenia <math>I_D >> I_S</math>. | ||
<math> | <math>g_D \approx \frac{I_D}{U_T}</math> | ||
potencjał elektrokinetyczny <math>U_T\,</math> w temperaturze 300 K jest równy około 26 mV | potencjał elektrokinetyczny <math>U_T\,</math> w temperaturze 300 K jest równy około 26 mV | ||
<math> | <math>U_T=\frac{kT}{e}=\frac{1,38\cdot 10^{-23} J/K \cdot 300K}{1,6\cdot 10^{-19}C}=25,875mV</math> | ||
Zatem szukana wartość konduktancji <math>g_D\,</math> jest równa | Zatem szukana wartość konduktancji <math>g_D\,</math> jest równa | ||
<math> | <math>g_D \approx \frac{I_D}{U_T}=\frac{3mA}{25,875mV}=0,0116S\approx 12mS</math> | ||
Pojemność dyfuzyjna diody Cd można obliczyć ze wzoru | Pojemność dyfuzyjna diody Cd można obliczyć ze wzoru | ||
<math> | <math>C_d=t_t \frac{e}{kT}(I_D+I_S)\approx t_t \frac{eI_D}{kT}=t_t \frac{I_D}{U_T}=t_t\cdot g_0=5ns\cdot 12mS=0,6nF</math> | ||
| Linia 205: | Linia 205: | ||
'''Rozwiązanie:''' | '''Rozwiązanie:''' | ||
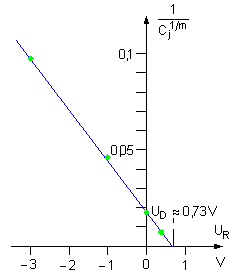
Metoda prób dobieramy wartość wykładnika m i rysujemy wykres funkcji <math> | Metoda prób dobieramy wartość wykładnika m i rysujemy wykres funkcji <math>\left( \frac{1}{C_j(U_R)}\right)^{-\frac{1}{m}}</math>, która powinna być linią prostą. Pojemność złącza obliczamy z zależności <math>C_j = C – C_0</math>. | ||
:[[Grafika:PEE_M13_Obraz1.gif]] | :[[Grafika:PEE_M13_Obraz1.gif]] | ||
| Linia 221: | Linia 221: | ||
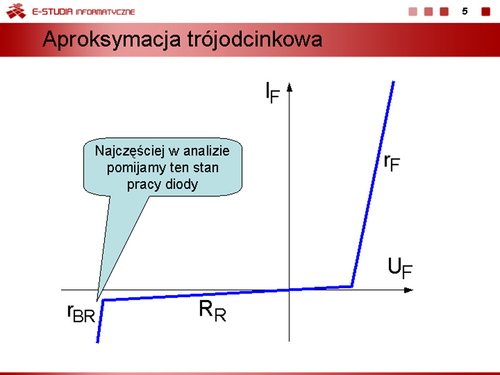
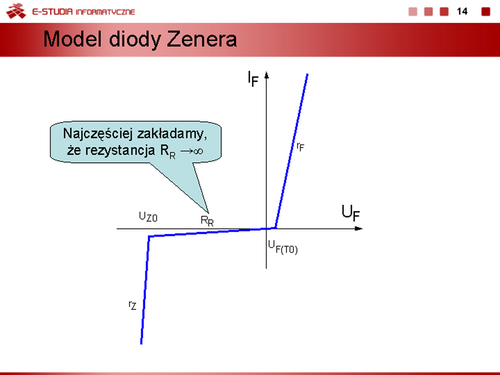
Czasami zakłada się, że pomiędzy punktami załączenia (napięcie progowe <math>U_{F(T0)}\,</math> w kierunku przewodzenia i przebicia (napięcie przebicia <math>U_{Z0}\,</math>) dla kierunku polaryzacji zaporowej stabilistor ma rezystancję <math>R_R\,</math> o kilka rzędów większą niż rezystancje <math>r_Z\,</math> i <math>r_F\,</math> | Czasami zakłada się, że pomiędzy punktami załączenia (napięcie progowe <math>U_{F(T0)}\,</math> w kierunku przewodzenia i przebicia (napięcie przebicia <math>U_{Z0}\,</math>) dla kierunku polaryzacji zaporowej stabilistor ma rezystancję <math>R_R\,</math> o kilka rzędów większą niż rezystancje <math>r_Z\,</math> i <math>r_F\,</math> | ||
Najczęściej przyjmuje się, że rezystancja <math> | Najczęściej przyjmuje się, że rezystancja <math>R_R\to \infty</math>. | ||
|} | |} | ||
| Linia 242: | Linia 242: | ||
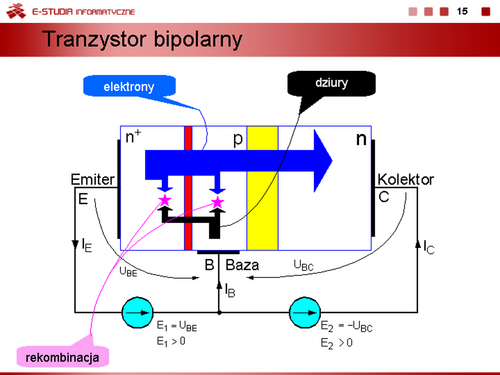
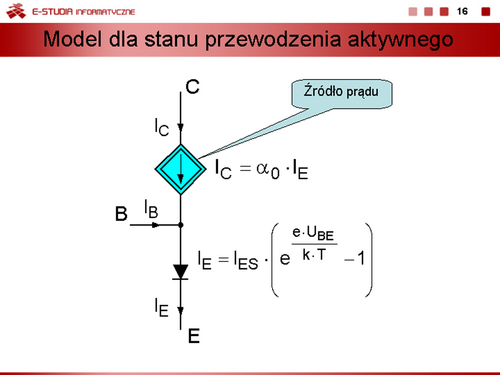
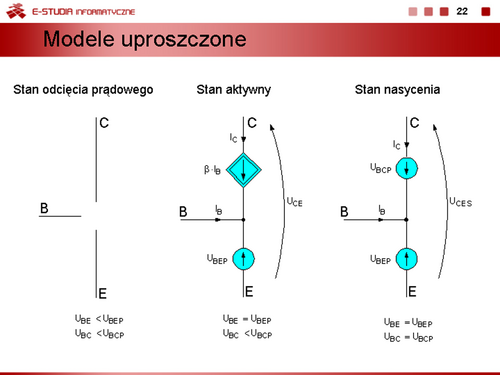
Dla tego stanu można zapisać: | Dla tego stanu można zapisać: | ||
<math> | <math>I_E=I_B+I_C=I_{ES}\bigg(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1\bigg)</math> | ||
<math> | <math>I_C=\beta_0\cdot I_B=\alpha_0\cdot I_E</math> | ||
<math> | <math>I_E=(\beta_0+1)I_B=\frac{I_C}{\alpha_0}</math> | ||
|} | |} | ||
| Linia 273: | Linia 273: | ||
|valign="top"|Można zatem zapisać równania, określające związki prądów <math>I_C\,</math>, <math>I_E\,</math> od napięć złączowych <math>U_{BE}\,</math>, <math>U_{BC}\,</math> w postaci | |valign="top"|Można zatem zapisać równania, określające związki prądów <math>I_C\,</math>, <math>I_E\,</math> od napięć złączowych <math>U_{BE}\,</math>, <math>U_{BC}\,</math> w postaci | ||
<math> | <math>I_E=I_{EN}-\alpha_I \cdot I_{CI}=I_{ES}\bigg(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)-\alpha_I\cdot I_{CS}\bigg(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | ||
<math> | <math>I_C=\alpha_N\cdot I_{EN}-I_{CI}=\alpha_N\cdot I_{ES}\bigg(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)- I_{CS}\bigg(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | ||
Równania te nazywamy równaniami Ebersa-Molla. | Równania te nazywamy równaniami Ebersa-Molla. | ||
| Linia 293: | Linia 293: | ||
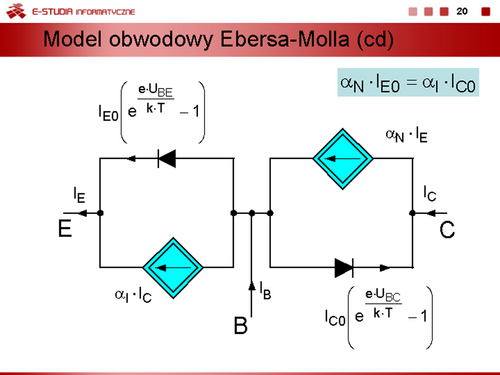
|valign="top"|Zwykle wygodniej jest posługiwać się modelem Ebersa-Molla, w którym sterowane źródła prądowe są uzależnione od prądów zewnętrznych tranzystora. | |valign="top"|Zwykle wygodniej jest posługiwać się modelem Ebersa-Molla, w którym sterowane źródła prądowe są uzależnione od prądów zewnętrznych tranzystora. | ||
<math> | <math>I_E=\alpha_I \cdot I_C+I_{E0}\bigg(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)</math> | ||
<math> | <math>I_C=\alpha_N \cdot I_E-I_{C0}\bigg(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | ||
gdzie <math> | gdzie <math>I_{E0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{ES}</math> | ||
:<math> | :<math>I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | ||
Prądy zerowe tranzystora <math>I_{C0} = I_{CB0},\, I_{E0} = I_{CE0}</math> nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że | Prądy zerowe tranzystora <math>I_{C0} = I_{CB0},\, I_{E0} = I_{CE0}</math> nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że | ||
<math> | <math>\alpha_N\cdot I_{E0}=\alpha_I\cdot I_{C0}</math> | ||
|} | |} | ||
| Linia 337: | Linia 337: | ||
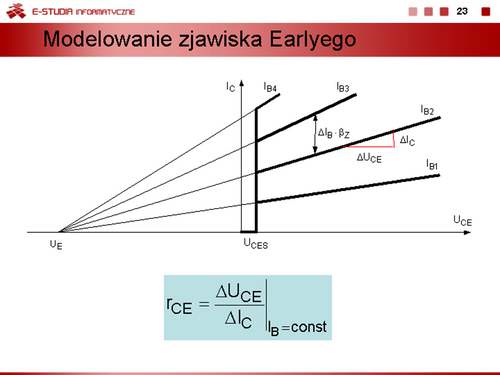
Uwzględniając potencjał <math>U_E\,</math> prąd kolektora można opisać zależnością: | Uwzględniając potencjał <math>U_E\,</math> prąd kolektora można opisać zależnością: | ||
<math> | <math>I_C=\beta_{N0}\bigg(1+\frac{U_{CE}}{U_E}\bigg)\cdot I_B=\beta_Z\cdot I_B</math> | ||
przy czym <math> | przy czym <math>\beta_Z=\beta_{N0}\bigg(1+\frac{U_{CE}}{U_E}\bigg)</math> | ||
<math>\beta_{N0}\,</math> – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy <math>U_{CE} = 0\, V\,</math>. | <math>\beta_{N0}\,</math> – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy <math>U_{CE} = 0\, V\,</math>. | ||
| Linia 345: | Linia 345: | ||
Znając potencjał Erlyego można wyznaczyć dynamiczną rezystancję wyjściową tranzystora | Znając potencjał Erlyego można wyznaczyć dynamiczną rezystancję wyjściową tranzystora | ||
<math> | <math>r_{CE}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}\approx \frac{U_E}{I_C}</math> | ||
|} | |} | ||
| Linia 374: | Linia 374: | ||
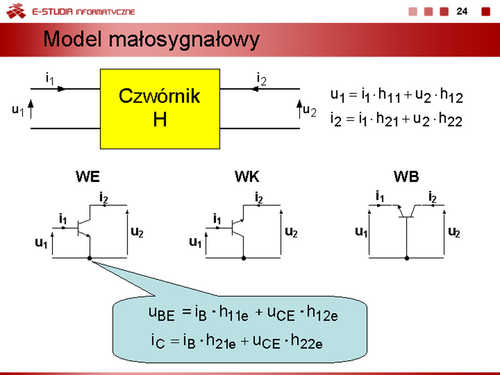
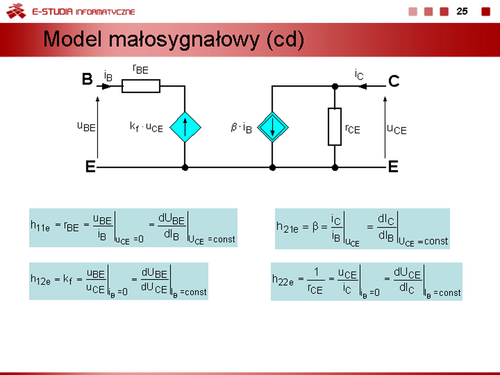
|valign="top"|Parametry hybrydowe tej macierzy często nazywane parametrami uniwersalnymi są definiowane następująco | |valign="top"|Parametry hybrydowe tej macierzy często nazywane parametrami uniwersalnymi są definiowane następująco | ||
<math> | <math>h_{11e}=r_{BE}=\frac{u_{BE}}{i_B}\bigg|_{u_{CE}=0}=\frac{dU_{BE}}{dI_B}\bigg|_{U_{CE}=const}</math> | ||
dynamiczna rezystancja wejściowa w stanie zwarcia na wyjściu, | dynamiczna rezystancja wejściowa w stanie zwarcia na wyjściu, | ||
<math> | <math>h_{12e}=k_f=\frac{u_{BE}}{u_{CE}}\bigg|_{i_B=0}=\frac{dU_{BE}}{dU_{CE}}\bigg|_{I_B=const}</math> | ||
współczynnik oddziaływania wstecznego w stanie rozwarcia na wejściu, | współczynnik oddziaływania wstecznego w stanie rozwarcia na wejściu, | ||
<math> | <math>h_{21e}=\beta=\frac{i_C}{i_B}\bigg|_{u_{CE=0}}=\frac{dI_C}{dI_B}\bigg|_{U_{CE}=const}</math> | ||
małosygnałowy współczynnik wzmocnienia prądowego w stanie zwarcia na wyjściu, | małosygnałowy współczynnik wzmocnienia prądowego w stanie zwarcia na wyjściu, | ||
<math> | <math>h_{22e}=\frac{1}{r_{CE}}=\frac{u_{CE}}{i_C}\bigg|_{i_B=0}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}</math> | ||
dynamiczna konduktancja (rezystancja) wyjściowa w stanie rozwarcia na wejściu. Schemat zastępczy tranzystora bipolarnego, w którym zastosowano parametry uniwersalne przedstawiono na slajdzie. | dynamiczna konduktancja (rezystancja) wyjściowa w stanie rozwarcia na wejściu. Schemat zastępczy tranzystora bipolarnego, w którym zastosowano parametry uniwersalne przedstawiono na slajdzie. | ||
| Linia 400: | Linia 400: | ||
Tranzystory JFET i MOSFET mają bardzo podobne charakterystyki. Zarówno dla jednych jak i drugich wyróżnia się zakres pracy liniowej i nieliniowej, które opisane są odpowiednio równaniami | Tranzystory JFET i MOSFET mają bardzo podobne charakterystyki. Zarówno dla jednych jak i drugich wyróżnia się zakres pracy liniowej i nieliniowej, które opisane są odpowiednio równaniami | ||
<math> | <math>I_D=\frac{I_{DSS}}{U_P^2}\left[2\cdot |U_{GS}-U_P|\cdot |U_{DS}|-U_{DS}^2\right]</math> dla zakresu pracy liniowej, | ||
<math> | <math>I_D=I_{DSS}\left(1-\bigg|\frac{U_{GS}}{U_P}\bigg| \right)^2</math> dla zakresu pracy nieliniowej. | ||
W modelach dla dużych sygnałów wykorzystuje się ten opis matematyczny tranzystora unipolarnego. | W modelach dla dużych sygnałów wykorzystuje się ten opis matematyczny tranzystora unipolarnego. | ||
| Linia 433: | Linia 433: | ||
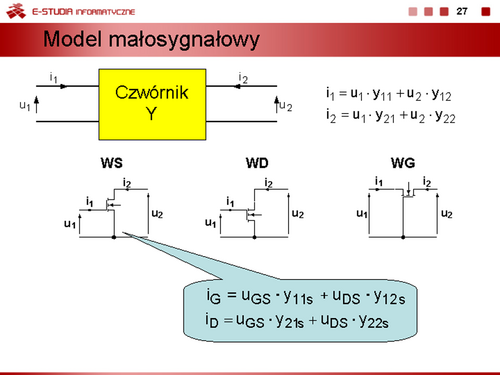
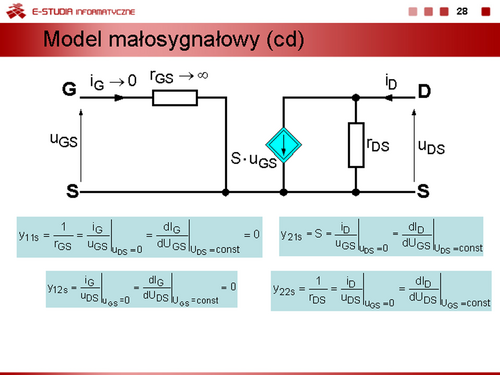
|valign="top"|W praktyce częściej zamiast parametrów admitancyjnych stosuje się parametry uniwersalne. Definicje tych parametrów są następujące: | |valign="top"|W praktyce częściej zamiast parametrów admitancyjnych stosuje się parametry uniwersalne. Definicje tych parametrów są następujące: | ||
<math> | <math>y_{11s}=\frac{1}{r_{GS}}=\frac{i_G}{u_{GS}}\bigg|_{u_{DS}=0}=\frac{dI_G}{dU_{GS}}\bigg|_{U_{DS}=const}=0</math> | ||
dynamiczna konduktancja wejściowa przy zwarciu na wyjściu (<math>r_{GS}\to \infty</math>), | dynamiczna konduktancja wejściowa przy zwarciu na wyjściu (<math>r_{GS}\to \infty</math>), | ||
<math> | <math>y_{12s}=\frac{i_G}{u_{DS}}\bigg|_{u_{GS}=0}=\frac{dI_G}{dU_{DS}}\bigg|_{U_{GS}=const}=0</math> | ||
oddziaływanie wsteczne (w tranzystorach unipolarnych nie występuje), | oddziaływanie wsteczne (w tranzystorach unipolarnych nie występuje), | ||
<math> | <math>y_{21s}=S=\frac{i_D}{u_{GS}}\bigg|_{u_{DS}=0}=\frac{dI_D}{dU_{GS}}\bigg|_{U_{DS}=const}</math> | ||
transkonduktancja dynamiczna (nachylenie charakterystyki bramkowej) przy zwarciu na wyjściu, | transkonduktancja dynamiczna (nachylenie charakterystyki bramkowej) przy zwarciu na wyjściu, | ||
<math> | <math>y_{22s}=\frac{1}{r_{DS}}=\frac{i_D}{u_{DS}}\bigg|_{u_{GS}=0}=\frac{dI_D}{dU_{DS}}\bigg|_{U_{GS}=const}</math> | ||
dynamiczna konduktancja, (rezystancja <math>r_{DS}\,</math>) wyjściowa przy zwarciu na wejściu. | dynamiczna konduktancja, (rezystancja <math>r_{DS}\,</math>) wyjściowa przy zwarciu na wejściu. | ||
Wersja z 08:56, 28 sie 2023
 |
Modele elementów półprzewodnikowych |
 |
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. |
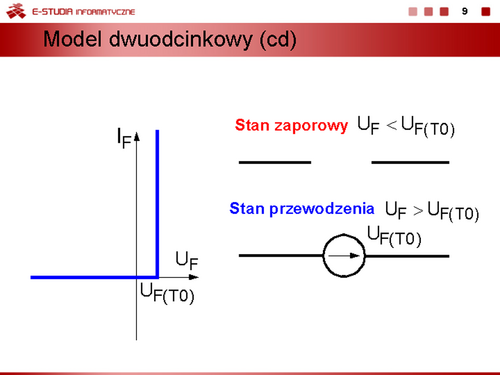 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
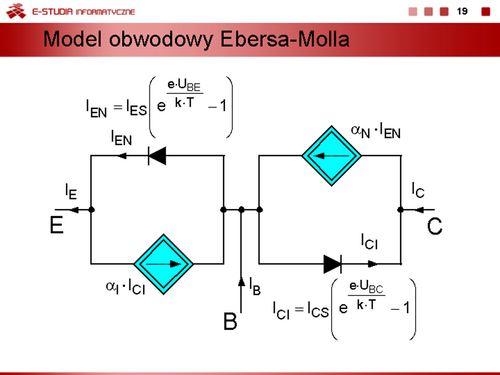 |
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976