PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 301: | Linia 301: | ||
:<math>\displaystyle I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | :<math>\displaystyle I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | ||
Prądy zerowe tranzystora <math>I_{C0} = I_{CB0},\, | Prądy zerowe tranzystora <math>I_{C0} = I_{CB0},\, I_{E0} = I_{CE0}</math> nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że | ||
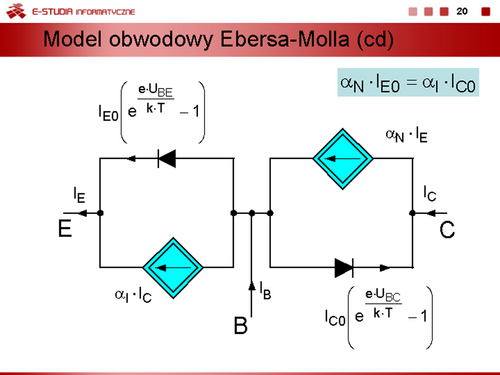
<math>\displaystyle \alpha_N\cdot I_{E0}=\alpha_I\cdot I_{C0}</math> | <math>\displaystyle \alpha_N\cdot I_{E0}=\alpha_I\cdot I_{C0}</math> | ||
| Linia 343: | Linia 343: | ||
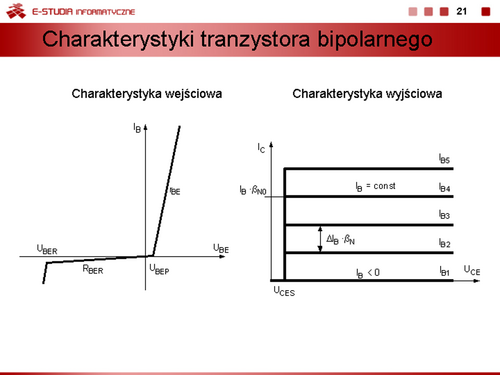
<math>\beta_{N0}\,</math> – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy <math>U_{CE} = 0\, V\,</math>. | <math>\beta_{N0}\,</math> – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy <math>U_{CE} = 0\, V\,</math>. | ||
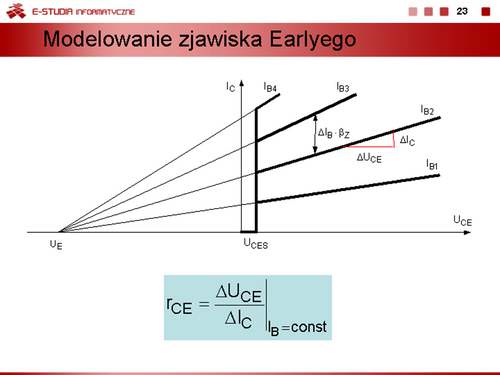
Znając potencjał Erlyego można wyznaczyć dynamiczną rezystancję wyjściową tranzystora | |||
<math>\displaystyle r_{CE}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}\approx \frac{U_E}{I_C}</math> | <math>\displaystyle r_{CE}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}\approx \frac{U_E}{I_C}</math> | ||
| Linia 454: | Linia 454: | ||
---- | ---- | ||
'''Literatura''' | |||
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | |||
Oficyna Wydawnicza PW, Warszawa 2005 | |||
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | |||
WNT, Warszawa 1981 | |||
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | |||
Wersja z 12:24, 16 sty 2007
 |
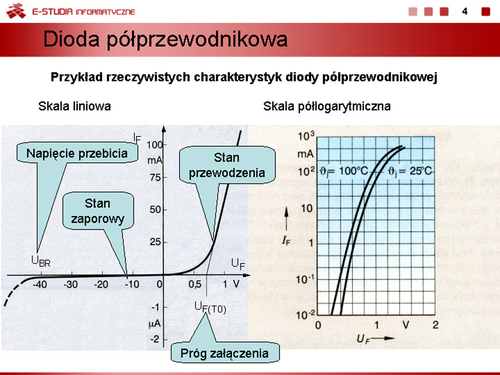
Modele elementów półprzewodnikowych |
 |
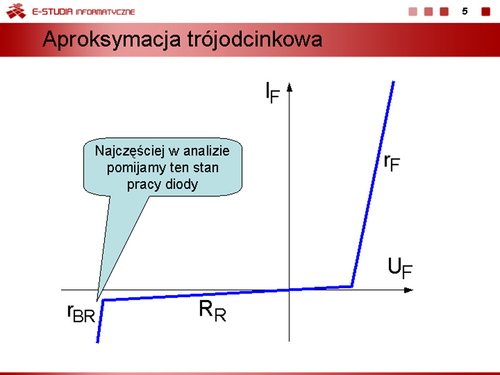
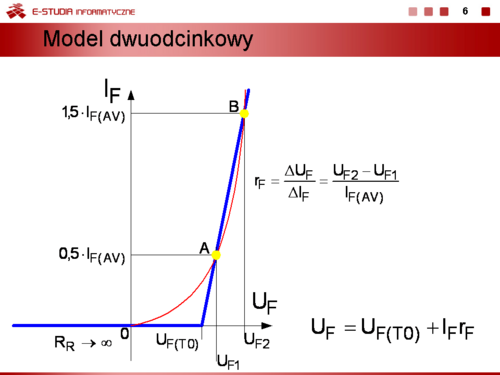
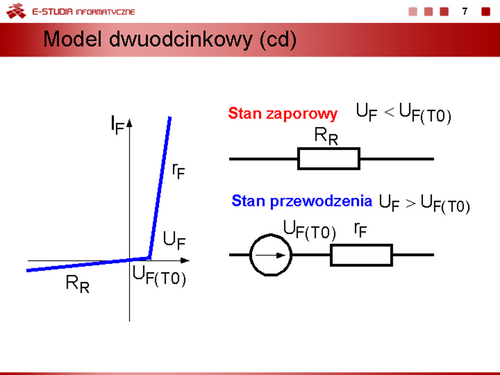
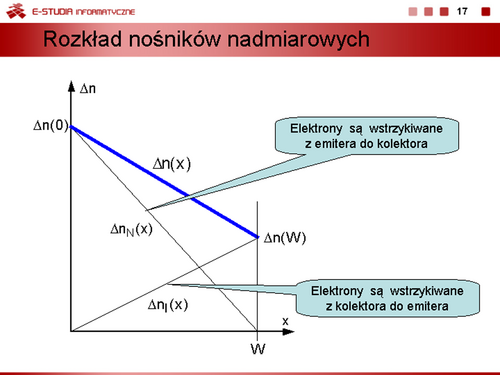
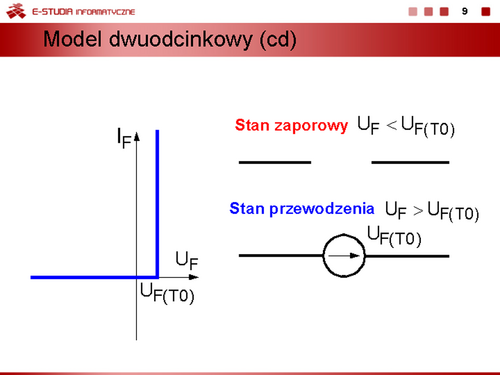
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. |
 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
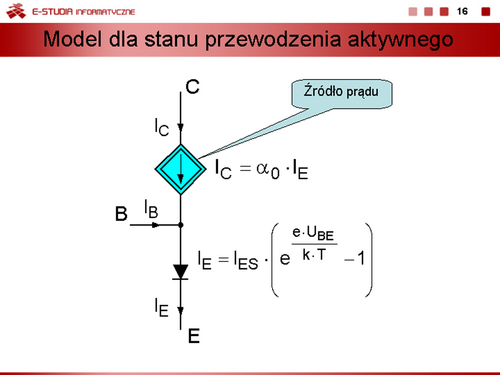
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
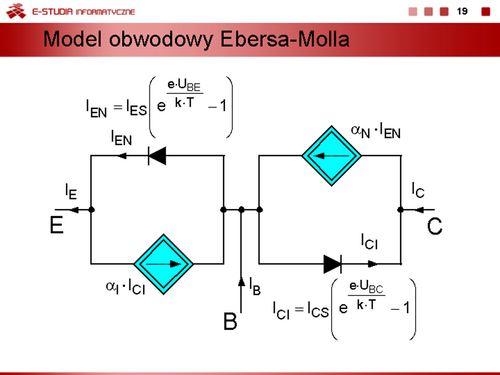 |
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976