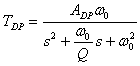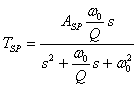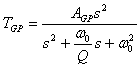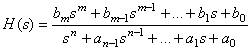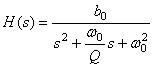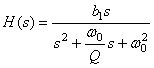PEE Lab 3: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 79: | Linia 79: | ||
Program badań: | Program badań: | ||
Wykreślić charakterystyki układu pierwszego rzędu: | Wykreślić charakterystyki układu pierwszego rzędu: | ||
* człon całkujący <math>H(s)=\frac{k}{s}</math>, | |||
* człon różniczkujący <math>H(s)=ks</math>, | |||
* przesuwnik fazowy <math>H(s)=\frac{(s-a)}{(s+a)}</math>, | |||
* człon inercyjny pierwszego rzędu <math>H(s)=\frac{(b_1 s+b_0)}{(a_1 s+a_0)}</math> przy dwu różnych wartościach parametrów założonych przez użytkownika. | |||
Wykreślić charakterystyki filtrów bikwadratowych (drugiego rzędu) | Wykreślić charakterystyki filtrów bikwadratowych (drugiego rzędu) | ||
dolnoprzepustowy | * dolnoprzepustowy | ||
[[Grafika:PEE_Lab_3_H_s_DP.gif]] | [[Grafika:PEE_Lab_3_H_s_DP.gif]] | ||
górnoprzepustowy | * górnoprzepustowy | ||
[[Grafika:PEE_Lab_3_H_s_SP.gif]] | [[Grafika:PEE_Lab_3_H_s_SP.gif]] | ||
środkowoprzepustowy | * środkowoprzepustowy | ||
[[Grafika:PEE_Lab_3_H_s_GP.gif]] | [[Grafika:PEE_Lab_3_H_s_GP.gif]] | ||
| Linia 103: | Linia 107: | ||
Wykreślić charakterystyki filtrów wyższego rzędu, np. czwartego i ósmego. Przykładowe transmitancje proponowane w badaniach | Wykreślić charakterystyki filtrów wyższego rzędu, np. czwartego i ósmego. Przykładowe transmitancje proponowane w badaniach | ||
[[Grafika:PEE_Lab_3_H_s_butt.gif]] | * Filtr Butterwortha: | ||
[[Grafika:PEE_Lab_3_H_s_butt.gif]] | |||
[[Grafika:PEE_Lab_3_H_s_butt_8.gif]] | [[Grafika:PEE_Lab_3_H_s_butt_8.gif]] | ||
* Filtr eliptyczny Cauera | |||
[[Grafika:PEE_Lab_3_H_s_cauer_4.gif]] | [[Grafika:PEE_Lab_3_H_s_cauer_4.gif]] | ||
[[Grafika:PEE_Lab_3_H_s_cauer_8.gif]] | [[Grafika:PEE_Lab_3_H_s_cauer_8.gif]] | ||
Zaobserwować charakterystyki amplitudowe w skali liniowej i logarytmicznej. | Zaobserwować charakterystyki amplitudowe w skali liniowej i logarytmicznej. | ||
| Linia 120: | Linia 125: | ||
C. Problemy do dyskusji: | C. Problemy do dyskusji: | ||
Napisać wyrażenie na transmitancję filtru bikwadratowego dolno | |||
Na podstawie wykreślonych charakterystyk amplitudowej i fazowej określić dobroć filtru i częstotliwość krytyczną. | * Napisać wyrażenie na transmitancję filtru bikwadratowego dolno, środkowo i górnoprzepustowego o następujących parametrach: <math>A=2</math>, <math>Q=2</math>, <math>f_0=1000Hz</math>, przy jednostkowych wzmocnieniach w pasmach przepustowych. | ||
Mając daną transmitancję operatorową filtru dolno, środkowo i górnoprzepustowego narysować charakterystyki amplitudowe i fazowe dla filtrów o transmitancjach | |||
* Na podstawie wykreślonych charakterystyk amplitudowej i fazowej określić dobroć filtru i częstotliwość krytyczną. | |||
* Mając daną transmitancję operatorową filtru dolno, środkowo i górnoprzepustowego narysować charakterystyki amplitudowe i fazowe dla filtrów o transmitancjach | |||
a) [[Grafika:PEE_Lab_3_H_zad1.gif]] | a) [[Grafika:PEE_Lab_3_H_zad1.gif]] | ||
| Linia 128: | Linia 136: | ||
c) [[Grafika:PEE_Lab_3_H_zad3.gif]] | c) [[Grafika:PEE_Lab_3_H_zad3.gif]] | ||
Literatura dodatkowa | ===Literatura dodatkowa=== | ||
1. Obwody elektryczne „Ćwiczenia laboratoryjne”, praca zbiorowa pod red. Stefana F. Filipowicza, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2002 | 1. Obwody elektryczne „Ćwiczenia laboratoryjne”, praca zbiorowa pod red. Stefana F. Filipowicza, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2002 | ||
Wersja z 07:24, 25 paź 2006
Ćwiczenie Nr 3: Badanie filtrów bikwadratowych i charakterystyk częstotliwościowych układów
Ćwiczenie jest ćwiczeniem wirtualnym. Student wykonuje pełny program badań przez Internet, wykorzystując opracowane do tego celu programy interakcyjne umieszczone poniżej
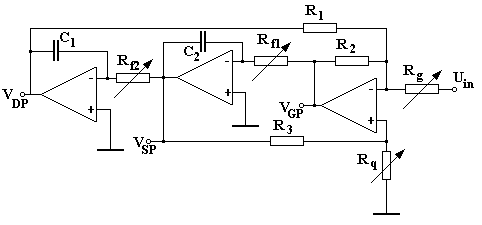
Badanie filtru bikwadratowego KHN
Schemat filtru KHN (Kerwina-Heulsmana-Newcomba [1]) wykorzystującego 3 wzmacniacze operacyjne przedstawiony jest na rys. 1.
Rys. 1 Schemat filtru bikwadratowego KHN
Filtr ten realizuje trzy podstawowe typy filtrów o następujących transmitancjach
Projektować będziemy filtr o zadanej wartości częstotliwości środkowej , dobroci oraz wartości wzmocnienia w paśmie . Dla zadanych wartości tych parametrów należy obliczyć wartości rezystancji rezystorów i pojemności kondensatorów korzystając z następujących wzorów:
Przy założeniu: , oraz Przyjmuje się: oraz lub . Wartości elementów oblicza się wg wzorów:
Na rys. 2 przedstawiono ikonę programu umożliwiającego zadawanie dowolnej wartości parametrów.
Rys. 2 Ikona programu do badania filtru KHN
Program badań:
Zaprojektować filtr KHN o podanych parametrach:
Filtr dolnoprzepustowy
Filtr środkowoprzepustowy
Filtr górnoprzepustowy
Zbadać jak wpływa zmiana o niewielkie wartości (do 10%) rezystorów , i na parametry filtru. Skorzystać z poniższej tabeli oznaczając strzałkami zmiany wielkości: ![]() (wzrost),
(wzrost), ![]() (zmniejszenie), b.z. (bez zmian). Badanie przeprowadzić dla 3 wybranych filtrów o różnych parametrach.
(zmniejszenie), b.z. (bez zmian). Badanie przeprowadzić dla 3 wybranych filtrów o różnych parametrach.
Badanie charakterystyk częstotliwościowych na podstawie transmitancji operatorowej
Badanie dotyczy charakterystyk częstotliwościowych układów dynamicznych opisanych transmitancją operatorową
Program „Charakterystyki” oblicza i wykreśla charakterystyki częstotliwościowe (amplitudową i fazową).
Program badań:
Wykreślić charakterystyki układu pierwszego rzędu:
- człon całkujący ,
- człon różniczkujący ,
- przesuwnik fazowy ,
- człon inercyjny pierwszego rzędu przy dwu różnych wartościach parametrów założonych przez użytkownika.
Wykreślić charakterystyki filtrów bikwadratowych (drugiego rzędu)
- dolnoprzepustowy
- górnoprzepustowy
- środkowoprzepustowy
dla dwu zadanych wartościach dobroci i jednej pulsacji środkowej .
Wykreślić charakterystyki filtrów wyższego rzędu, np. czwartego i ósmego. Przykładowe transmitancje proponowane w badaniach
- Filtr Butterwortha:
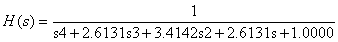

- Filtr eliptyczny Cauera
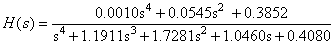
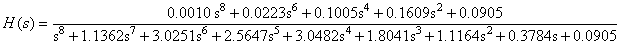
Zaobserwować charakterystyki amplitudowe w skali liniowej i logarytmicznej.
C. Problemy do dyskusji:
- Napisać wyrażenie na transmitancję filtru bikwadratowego dolno, środkowo i górnoprzepustowego o następujących parametrach: , , , przy jednostkowych wzmocnieniach w pasmach przepustowych.
- Na podstawie wykreślonych charakterystyk amplitudowej i fazowej określić dobroć filtru i częstotliwość krytyczną.
- Mając daną transmitancję operatorową filtru dolno, środkowo i górnoprzepustowego narysować charakterystyki amplitudowe i fazowe dla filtrów o transmitancjach
Literatura dodatkowa
1. Obwody elektryczne „Ćwiczenia laboratoryjne”, praca zbiorowa pod red. Stefana F. Filipowicza, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2002