Układy elektroniczne i technika pomiarowa/Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 395: | Linia 395: | ||
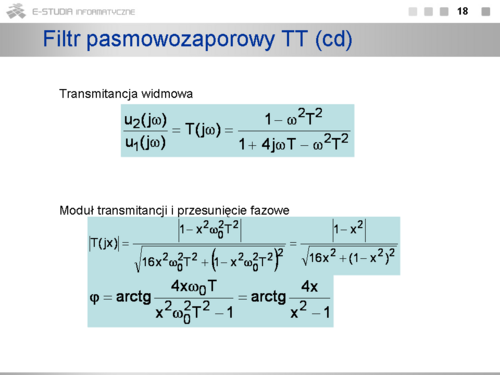
<math>|T(jx)|=\frac{|1-x^2\omega_0^2LC|}{\sqrt { x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{|1-x^2|}{\sqrt{x^2+(1-x^2)^2}}</math> | <math>|T(jx)|=\frac{|1-x^2\omega_0^2LC|}{\sqrt { x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{|1-x^2|}{\sqrt{x^2+(1-x^2)^2}}</math> | ||
Charakterystycznym parametrem filtrów pasmowych i rezonansowych jest pasmo przenoszenia B i dobroć filtru Q, definiowana jako: | Charakterystycznym parametrem filtrów pasmowych i rezonansowych jest pasmo przenoszenia B i dobroć filtru Q, definiowana jako: | ||
<math>Q=\frac{f_0}{B}</math> , gdzie f0 częstotliwość rezonansowa lub częstotliwość środkowa filtru. | <math>Q=\frac{f_0}{B}</math> , gdzie f0 częstotliwość rezonansowa lub częstotliwość środkowa filtru. | ||
| Linia 409: | Linia 404: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd23.png|thumb|500px]] | ||
|valign="top"|'''Filtry aktywne''' | |valign="top"|'''Filtry aktywne''' | ||
| Linia 423: | Linia 418: | ||
• łatwe i niezależne strojenie parametrów filtru (częstotliwość, wzmocnienie, dobroć) | • łatwe i niezależne strojenie parametrów filtru (częstotliwość, wzmocnienie, dobroć) | ||
• możliwość budowy filtrów uniwersalnych. | • możliwość budowy filtrów uniwersalnych. | ||
|} | |} | ||
| Linia 429: | Linia 424: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd24.png|thumb|500px]] | ||
|valign="top"|'''Filtry dolnoprzepustowe i górnoprzepustowe I rzędu''' | |valign="top"|'''Filtry dolnoprzepustowe i górnoprzepustowe I rzędu''' | ||
| Linia 461: | Linia 456: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd25.png|thumb|500px]] | ||
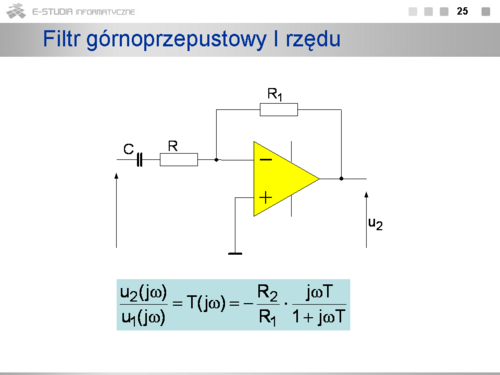
|valign="top"|'''Filtr górnoprzepustowy''' | |valign="top"|'''Filtr górnoprzepustowy''' | ||
| Linia 517: | Linia 512: | ||
<math>\frac{C_2}{C_1}>\frac{4b_1(1-k_u_0)}{a_1^2}</math> | <math>\frac{C_2}{C_1}>\frac{4b_1(1-k_u_0)}{a_1^2}</math> | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd26.png|thumb|500px]] | |||
|valign="top"| | |||
Wersja z 12:40, 24 paź 2006
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |