SW wykład 12 - Slajd11

<<powrót do strony wykładu

Zadanie programistyczne Przykład Problemy z logiką Hoare'a Poprawność całkowita Poprawność całkowita, c.d. Poprawność całkowita, c.d. Reguła dla pętli Poprawność systemu dowodzenia dla Tiny Pełność systemu dowodzenia dla Tiny Przykład Uogólnienie Poprawność i pełność Relacje dobrze ufundowane Dowodzenie poprawności całkowitej Przykład Przykład Kolejny problem Binarne warunki końcowe Warunki poprawności Reguły dowodzenia Reguły dowodzenia, c.d. Przykład Logika algorytmiczna System dowodzenia

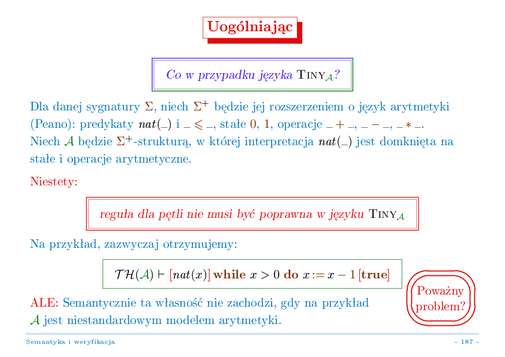
Przypomnijmy, że na poprzednim wykładzie (wykład 11, slajdy 5, 6) wprowadziliśmy pewne uogólnienie naszego języka TINY zastępując w nim liczby całkowite z odpowiednimi predykatami i operacjami arytmetycznymi dowolnym pierwotnym typem danych określonym jako algebra nad dowolną sygnaturą. Wszelkie pojęcia semantyczne wprowadzone dla języka TINY przenoszą się w sposób oczywisty na takie jego uogólnienie. Dotyczy to także pojęcia całkowitej poprawności instrukcji języka względem warunków wstępnego i końcowego zadanych formułami pierwszego rzędu.

Zastanówmy się jeszcze, jak system dowodzenia dla stwierdzeń całkowitej poprawności można stosować dla takiego uogólnienia języka TINY na dowolny pierwotny typ danych. Problemem jest reguła dla instrukcji pętli, której na ogół nie da się nawet sformułować dla dowolnego pierwotnego typu danych. Dlatego też wymagać tu będziemy, by pierwotny typ danych "definiował" predykaty i operacje arytmetyczne wykorzystywane w podstawowej wersji języka TINY. Dla dowolnej sygnatury wprowadzamy zatem jej rozszerzenie o odpowiednie predykaty, stałe i operacje arytmetyczne, rozważamy dowolną algebrę nad tak rozszerzoną sygnaturą, i rozpatrujemy uogólnienie języka TINY tylko dla takich pierwotnych typów danych.

Niestety, jak łatwo się przekonać, reguła dla instrukcji pętli w tak uogólnionym języku nie musi być poprawna: może pozwolić na "dowód" nieprawdziwych stwierdzeń całkowitej poprawności instrukcji. Problem w tym, że z powyższej konstrukcji nie wynika, że zasada indukcji może być stosowana dla wartości pierwotnego typu danych interpretowanych jako liczby naturalne (określeniu tych wartości służy predykat $nat$).