MN11

Funkcje sklejane (splajny)

<<< Powrót do strony głównej przedmiotu Metody numeryczne

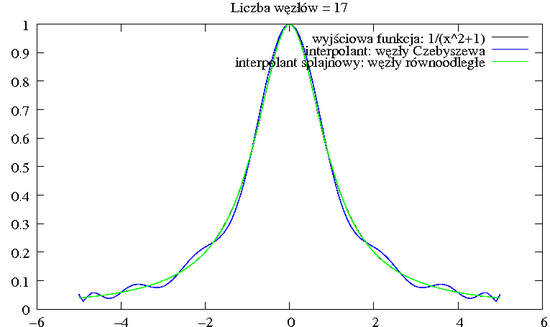
Interpolacja wielomianami interpolacyjnymi, chociaż korzysta z funkcji gładkich i łatwo reprezentowalnych w komputerze, ma jednak również pewne wady. Zauważmy, że błąd interpolacji może być bardzo duży (zjawisko Rungego), a poza tym interpolacja jest nielokalna: nawet mała zmiana warości funkcji w pojedynczym węźle może powodować dużą zmianę zachowania całego wielomianu interpolacyjnego. Czasem więc lepiej jest zastosować innego rodzaju interpolację, np. posługując się funkcjami sklejanymi, które tylko lokalnie są wielomianami, sklejonymi w taki sposób, by globalnie zachować pewien stopień gładkości, tzn. różniczkowalność zadaną liczbę razy.

Tego typu podejście okazało się bardzo owocne m.in. w grafice komputerowej (np. dla wizualizacji scenerii w grach komputerowych), a także np. posłużyło jako narzędzie konstrukcji skalowalnych czcionek komputerowych w Postscripcie (precyzyjniej, korzysta się tam z tzw. krzywych Beziera --- pewnych krzywych sklejanych zadanych na płaszczyźnie). Z krzywych Beziera powszechnie korzysta się również w systemach CAD (Computer Aided Design).

Zamiast terminu funkcje sklejane używa się też często terminów splajny (spline), albo funkcje gięte. Nazwy te biorą się stąd, że zadanie interpolacji naturalnym splajnem kubicznym można interpretować jako model matematyczny aparatu służącego do wytwarzania mebli giętych.

Funkcje sklejane

W ogólności przez funkcję sklejaną rozumie się każdą funkcję przedziałami wielomianową. Nas będą jednak interesować szczególne funkcje tego typu i dlatego termin funkcje sklejane zarezerwujemy dla funkcji przedziałami wielomianowych i posiadających dodatkowe własności, które teraz określimy.

Niech dany będzie przedział skończony $[a,b]$ i węzły

$a=x_0<x_1<\cdots <x_n=b,$

przy czym $n\ge 1$.

Definicja

Funkcję $s:R\to R$ nazywamy funkcją sklejaną rzędu $r$ ($r\ge 1$) odpowiadającą węzłom $x_j$, $0\le j\le n$, jeśli spełnione są następujące dwa warunki:

(i)

$s$ jest wielomianem stopnia co najwyżej $2r-1$ na każdym

z przedziałów $[x_{j-1},x_j]$, tzn. $s_{|[x_{j-1},x_j]}\in {\mathrm{\Pi }}_{2r-1}$, $1\le j\le n$,

(ii)

$s$ jest $(2r-2)$-krotnie różniczkowalna w sposób

ciągły na całej prostej, tzn. $s\in C^{(2r-2)}(R)$.

Jeśli ponadto

(iii)

$s$ jest wielomianem stopnia co najwyżej $r-1$ poza

$(a,b)$, tzn. $s_{|(-\mathrm{\infty },a]},s_{|[b,+\mathrm{\infty })}\in {\mathrm{\Pi }}_{r-1}$,

to $s$ jest naturalną funkcją sklejaną.

Klasę naturalnych funkcji sklejanych rzędu $r$ opartych na węzłach $x_j$ będziemy oznaczać przez ${{𝒮}}_r(x_0,\dots ,x_n)$, albo po prostu ${{𝒮}}_r$, jeśli węzły są ustalone.

Na przykład funkcją sklejaną rzędu pierwszego ($r=1$) jest funkcja ciągła i liniowa na poszczególnych przedziałach $[x_{j-1},x_j]$. Jest ona naturalna, gdy poza $(a,b)$ jest funkcją stała. Tego typu funkcje nazywamy liniowymi funkcjami sklejanymi.

Najważniejszymi z praktycznego punktu widzenia są jednak funkcje sklejane rzędu drugiego odpowiadające $r=2$. Są to funkcje, które są na $R$ dwa razy różniczkowalne w sposób ciągły, a na każdym z podprzedziałów są wielomianami stopnia co najwyżej trzeciego. W tym przypadku mówimy o kubicznych funkcjach sklejanych. Funkcja sklejana kubiczna $s$ jest naturalna, gdy poza $(a,b)$ jest wielomianem liniowym, a więc $s^{″}(a)=s^{″}(b)=0$.

Interpolacja i gładkość

Pokażemy najpierw ważny lemat, który okaże się kluczem do dowodu dalszych twierdzeń.

Niech $W^r(a,b)$ będzie klasą funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:[a,b]\toR} takich, że $f$ jest $(r-1)$ razy różniczkowalna na $[a,b]$ w sposób ciągły oraz $f^{(r)}(x)$ istnieje prawie wszędzie na $[a,b]$ i jest całkowalna z kwadratem, tzn.

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned W^r(a,b) &= \{\,f\in C^{(r-1)}([a,b]):\, f^{(r)}(x) \mbox{ istnieje p.w. na } [a,b] \\ && \qquad\qquad\qquad\qquad \mbox{ oraz } f^{(r)}\in{\cal L}_2(a,b)\,\}. \endaligned}

Oczywiście każda funkcja sklejana rzędu $r$ (niekoniecznie naturalna) należy do $W^r(a,b)$.

Lemat

Niech $f\in W^r(a,b)$ będzie funkcją zerującą się w węzłach, tzn.

$f(x_j)=0,0\le j\le n.$

Wtedy dla dowolnej naturalnej funkcji sklejanej $s\in {{𝒮}}_r$ mamy

$\underset{a}{\overset{b}{\int }}{f}^{(r)}(x)s^{(r)}(x)dx=0.$

Dowód

Dla $r=1$ funkcja $s^{\prime }$ jest przedziałami stała. Oznaczając przez $a_j$ jej wartość na $[x_{j-1},x_j]$ dostajemy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \int_a^b f'(x)s'(x)\,dx &= \sum_{j=1}^n\int_{t_{j-1}}^{t_j} f'(x)a_j\,dx \\ &= \sum_{j=1}^n a_j(f(x_j)-f(x_{j-1}))\,=\,0, \endaligned}

ponieważ $f$ zeruje się w $t_j$.

Rozpatrzmy teraz przypadek $r\ge 2$. Ponieważ

$(f^{(r-1)}{s}^{(r)}{)}^{\prime }=f^{(r)}{s}^{(r)}+f^{(r-1)}{s}^{(r+1)},$

to

$\underset{a}{\overset{b}{\int }}{f}^{(r)}(x)s^{(r)}(x)dx=f^{(r-1)}(x)s^{(r)}(x){|}_a^b-\underset{a}{\overset{b}{\int }}{f}^{(r-1)}(x)s^{(r+1)}(x)dx.$

Wobec tego, że $s$ jest poza przedziałem $(a,b)$ wielomianem stopnia co najwyżej $r-1$ oraz $s^{(r)}$ jest ciągła na $R$, mamy $s^{(r)}(a)=0=s^{(r)}(b)$, a stąd

$f^{(r-1)}(x)s^{(r)}(x){|}_a^b=0.$

Postępując podobnie, tzn. całkując przez części $r-1$ razy, otrzymujemy w końcu

$\underset{a}{\overset{b}{\int }}{f}^{(r)}(x)s^{(r)}(x)dx=(-1{)}^{r-1}\underset{a}{\overset{b}{\int }}{f}^{\prime }(x)s^{(2r-1)}(x)dx.$

Funkcja $s^{(2r-1)}$ jest przedziałami stała, a więc możemy teraz zastosować ten sam argument jak dla $r=1$, aby pokazać,

że ostatnia całka jest równa zeru.

Funkcje sklejane chcielibyśmy zastosować do interpolacji funkcji. Ważne jest więc, aby odpowiednie zadanie interpolacyjne miało jednoznaczne rozwiązanie.

Twierdzenie O istnieniu i jednoznaczności naturalnego splajnu interpolacyjnego

Jeśli $n+1\ge r$, to dla dowolnej funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:[a,b]\toR} istnieje dokładnie jedna naturalna funkcja sklejana $s_f\in {{𝒮}}_r$ interpolująca $f$ w węzłach $x_j$, tzn. taka, że

$s_f(x_j)=f(x_j),0\le j\le n.$

Dowód

Pokażemy najpierw, że jedyną naturalną funkcją sklejaną interpolującą dane zerowe jest funkcja zerowa. Rzeczywiście, jeśli $s(x_j)=0$ dla $0\le j\le n$, to podstawiając w poprzednim lemacie $f=s$, otrzymujemy

$\underset{a}{\overset{b}{\int }}(s^{(r)}(x){)}^{2}dx=0.$

Stąd $s^{(r)}$ jest funkcją zerową, a więc $s$ jest wielomianem stopnia co najwyżej $r-1$ zerującym się w co najmniej $n+1$ punktach $x_j$. Wobec tego, że $n+1>r-1$, otrzymujemy $s\equiv 0$.

Zauważmy teraz, że problem znalezienia naturalnej funkcji sklejanej $s$ interpolującej $f$ można sprowadzić do rozwiązania układu równań liniowych z macierzą kwadratową. Na każdym przedziale $[x_{i-1},x_i]$, $1\le i\le n$, jest ona postaci

$s(x)=w_i(x)=\sum _{j=0}^{2r-1}{a}_{i,j}{x}^j,$

dla pewnych współczynników Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle a_{i,j}\inR} , a na $(-\mathrm{\infty },a]$ i $[b,\mathrm{\infty })$ mamy odpowiednio

$s(x)=w_0(x)=\sum _{j=0}^{r-1}{a}_{0,j}{x}^j$

i

$s(x)=w_{n+1}(x)=\sum _{j=0}^{r-1}{a}_{n+1,j}{x}^j.$

Aby wyznaczyć $s$, musimy więc znaleźć ogółem $2r(n+1)$ współczynników $a_{i,j}$, przy czym są one związane $(2r-1)(n+1)$ warunkami jednorodnymi wynikającymi z gładkości,

$w_i^{(k)}(x_i)=w_{i+1}^{(k)}(x_i)$

dla $0\le i\le n$ i $0\le k\le 2r-2$, oraz $n+1$ niejednorodnymi warunkami interpolacyjnymi,

$w_i(x_i)=f(x_i)$

dla $0\le i\le n$. Otrzymujemy więc układ $2r(n+1)$ równań liniowych ze względu na $2r(n+1)$ niewiadomych $a_{i,j}$.

Naturalna funkcja sklejana interpolująca $f$ jest wyznaczona jednoznacznie wtedy i tylko wtedy, gdy układ ten ma jednoznaczne rozwiązanie. To zaś zachodzi, gdy zero jest jedynym rozwiązaniem układu jednorodnego. Rzeczywiście, układ jednorodny odpowiada zerowym warunkom interpolacyjnym, przy których, jak pokazaliśmy wcześniej, zerowa funkcja sklejana (której odpowiada $a_{i,j}=0$, $\mathrm{\forall }i,j$) jest jedynym rozwiązaniem zadania interpolacyjnego.

Naturalnych funkcji sklejanych możemy więc używać do interpolacji funkcji. Pokażemy teraz inną ich własność, która jest powodem dużego praktycznego zainteresowania funkcjami sklejanymi.

Twierdzenie O ekstremalnej własności splajnów naturalnych

Niech $f\in W^r(a,b)$ i niech $s_f\in {{𝒮}}_r$ będzie naturalną funkcją sklejaną rzędu $r$ interpolującą $f$ w węzłach $x_j$, $0\le j\le n$. Wtedy

$\underset{a}{\overset{b}{\int }}(f^{(r)}(x){)}^{2}dx\ge \underset{a}{\overset{b}{\int }}(s_f^{(r)}(x){)}^{2}dx.$

Dowód

Jeśli przedstawimy $f$ w postaci $f=s_f+(f-s_f)$, to

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \int_a^b\Big(f^{(r)}(x)\Big)^2\,dx &= \int_a^b\Big(s_f^{(r)}(x)\Big)^2\,dx\,+\, \int_a^b\Big((f-s_f)^{(r)}(x)\Big)^2\,dx \\ & & \qquad\qquad + 2\,\int_a^b s_f^{(r)}(x)(f-s_f)^{(r)}(x)\,dx. \endaligned}

Funkcja $f-s_f$ jest w klasie $W^r(a,b)$ i zeruje się w węzłach $x_j$, $0\le j\le n$. Z lematu wynika więc, że

$\underset{a}{\overset{b}{\int }}{s}_f^{(r)}(x)(f-s_f{)}^{(r)}(x)dx=0$, a stąd wynika teza.

Wartość całki $\underset{a}{\overset{b}{\int }}(f^{(r)}(x){)}^{2}dx$ może być w ogólności uważana za miarę gładkości funkcji. Dowiedzioną nierówność możemy więc zinterpretować w następujący sposób. Naturalna funkcja sklejana jest w klasie $W^r(a,b)$ najgładszą funkcją spełniającą dane warunki interpolacyjne w wybranych węzłach $x_j$.

Jak już wspomnieliśmy, najczęściej używanymi są kubiczne funkcje sklejane. Dlatego rozpatrzymy je oddzielnie.

Kubiczne funkcje sklejane

Jeśli zdecydowaliśmy się na użycie kubicznych funkcji sklejanych, powstaje problem wyznaczenia $s_f\in {{𝒮}}_2$ interpolującej daną funkcję $f$, tzn. takiej, że $s_f(x_i)=f(x_i)$ dla $0\le i\le n$. W tym celu, na każdym przedziale $[x_i,x_{i+1}]$ przedstawimy $s_f$ w postaci jej rozwinięcia w szereg Taylora w punkcie $x_i$,

$s_f(x)=w_i(x)=a_i+b_i(x-x_i)+c_i\frac{(x-x_i{)}^2}{2}+d_i\frac{(x-x_i{)}^3}{6},$

i podamy algorytm obliczania $a_i,b_i,c_i,d_i$ dla $0\le i\le n-1$.

Warunki brzegowe i warunki ciągłości dla ${s_f}^{″}$ dają nam ${w_0}^{″}(x_0)=0=w_{n^{″}-1}(x_n)$ oraz ${w_i}^{″}(x_{i+1})=w_{i^{″}+1}(x_{i+1})$, czyli

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned c_0 &= 0, \\ c_i+d_ih_i &= c_{i+1}, \qquad 0\le i\le n-2, \\ c_{n-1}+d_{n-1}h_{n-1} &= 0, \endaligned}

gdzie $h_i=x_{i+1}-x_i$. Stąd, przyjmując dodatkowo $c_n=0$, otrzymujemy

$d_i=\frac{c_{i+1}-c_i}{h_i},1\le i\le n-1.$

Z warunków ciągłości dla ${s_f}^{\prime }$ dostajemy z kolei

$b_i+c_i{h}_i+d_i\frac{h_i^2}{2}=b_{i+1},0\le i\le n-2,$

oraz

$b_{i+1}=b_i+h_i\frac{c_{i+1}+c_i}{2},0\le i\le n-2.$

Warunki ciągłości $s_f$ dają w końcu

$a_i+b_i{h}_i+c_i\frac{h_i^2}{2}+d_i\frac{h_i^3}{6}=a_{i+1},0\le i\le n-2.$

Powyższe równania definiują nam na odcinku $[a,b]$ naturalną kubiczną funkcję sklejaną. Ponieważ poszukiwana funkcja sklejana $s_f$ ma interpolować $f$, mamy dodatkowych $n+1$ warunków interpolacyjnych $w_i(x_i)=f(x_i)$, $0\le i\le n-1$, oraz $w_{n-1}(x_n)=f(x_n)$, z których

$a_i=f(x_i),0\le i\le n-1.$

Teraz możemy warunki ciągłości przepisać jako

$f(x_{i+1})=f(x_i)+b_i{h}_i+c_i{h}_i^2+d_i\frac{h_i^3}{6},$

przy czym wzór ten zachodzi również dla $i=n-1$. Po wyrugowaniu $b_i$ i podstawieniu $d_i$, mamy

$b_i=f(x_i,x_{i+1})+h_i\frac{c_{i+1}+2c_i}{6},0\le i\le n-1,$

gdzie $f(x_i,x_{i+1})$ jest odpowiednią różnicą dzieloną. Możemy teraz powyższe wyrażenie na $b_i$ podstawić, aby otrzymać

$c_i\frac{h_i}{6}+c_{i+1}\frac{h_i+h_{i+1}}{3}+c_{i+1}\frac{h_{i+1}}{6}=f(x_{i+1},x_{i+2})-f(x_i,x_{i+1}).$

Wprowadzając oznaczenie

$c_i^{*}=\frac{c_i}{6},$

możemy to równanie przepisać jako

$\frac{h_i}{h_i+h_{i+1}}{c}_i^{*}+2c_{i+1}^{*}+\frac{h_{i+1}}{h_i+h_{i+1}}{c}_{i+2}^{*}=f(x_i,x_{i+1},x_{i+2}),$

$0\le i\le n-2$, albo w postaci macierzowej

$\left(\begin{array}{cc}2& w_1\\ u_2& 2& w_2\\ & u_3& 2& w_3\\ & & \ddots & \ddots & \ddots \\ & & & u_{n-2}& 2& w_{n-2}\\ & & & & u_{n-1}& 2\end{array}\right)\left(\begin{array}{c}{c}_1^{*}\\ c_2^{*}\\ c_3^{*}\\ ⋮\\ c_{n-2}^{*}\\ c_{n-1}^{*}\end{array}\right)=\left(\begin{array}{c}{v}_1\\ v_2\\ v_3\\ ⋮\\ v_{n-2}\\ v_{n-1}\end{array}\right),$

gdzie

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned && u_i\,=\,\frac{h_{i-1}}{h_{i-1}+h_i},\qquad w_i\,=\,\frac{h_i}{h_{i-1}+h_i}, \\ && v_i\,=\,f(x_{i-1},x_i,x_{i+1}). \endaligned}

Ostatecznie, aby znaleźć współczynniki $a_i,b_i,c_i,d_i$ należy najpierw rozwiązać układ równań liniowych, a potem zastosować wzory definiujące pozostałe współczynniki.

Zauważmy, że macierz układu równań liniowych jest trójdiagonalna i ma dominującą przekątną. Układ można więc rozwiązać kosztem proporcjonalnym do wymiaru $n$ używając algorytmu przeganiania. Koszt znalezienia wszystkich współczynników kubicznej funkcji sklejanej interpolującej $f$ jest więc też proporcjonalny do $n$.

MATLAB i Octave mają wbudowaną funkcję wyznaczającą naturalny kubiczny splajn interpolujący zadane wartości:

s = spline(x,y);

Aby wyznaczyć wartości takiego splajnu w zadanych punktach $X$, także musimy użyć specjalnej funkcji,

Y = ppval(s,X);

Na końcu oszacujemy jeszcze błąd interpolacji naturalnymi kubicznymi funkcjami sklejanymi na przedziale $[a,b]$. Będziemy zakładać, że $f$ jest dwa razy różniczkowalna w sposób ciągły.

Twierdzenie O błędzie interpolacji splajnem kubicznym

Jeśli $f\in F_M^1([a,b])$ to

$\Vert f-s_f{\Vert }_{C([a,b])}\le 5M\underset{1\le i\le n}{\max }(x_i-x_{i-1}{)}^2.$

W szczególności, dla podziału równomiernego $x_i=a+i\frac{b-a}{n}$, $0\le i\le n$, mamy

$\Vert f-s_f{\Vert }_{C([a,b])}\le 5M(\frac{b-a}{n}{)}^2.$

Dowód

Wykorzystamy obliczoną wcześniej postać interpolującej funkcji sklejanej $s_f$. Dla $x\in [x_i,x_{i+1}]$ mamy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned w_i(x) &= f(x_i)\,+\,\left(\frac{f(x_{i+1})-f(x_i)}{h_i} -h_i(c_{i+1}^*+2c_i^*)\right)(x-x_i) \\ &&\qquad\qquad \,+\, 3c_i^*(x-x_i)^2\,+\,\frac{c_{i+1}^*-c_i^*}{h_i}(x-x_i)^3. \endaligned}

Z rozwinięcia $f$ w szereg Taylora w punkcie $x_i$ dostajemy $f(x)=f(x_i)+f^{\prime }(x_i)(x-x_i)+f^{″}({\xi }_1)(x-x_i{)}^2/2$ oraz $(f(x_{i+1})-f(x_i))/h_i=f^{\prime }(x_i)+h_i{f}^{″}({\xi }_2)/2$. Stąd

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \lefteqn{f(x)-s_f(x) \,=\, f(x)-w_i(x)} \\ &= \frac{f''(\xi_1)}2(x-x_i)^2-\left(\frac{f''(\xi_2)}2 -(c_{i+1}^*+2c_i^*)\right)h_i(x-x_i) \\ & & \qquad\qquad\qquad -3c_i^*(x-x_i)^2 -\frac{c_{i+1}^*-c_i^*}{h_i}(x-x_i)^3, \endaligned}

oraz

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned |f(x)-s_f(x)| &\le &(M+2|c_{i+1}^*|+6|c_i^*|)h_i^2 \\ &= (M+8\max_{1\le i\le n-1}|c_i^*|)h_i^2. \endaligned}

Niech teraz $\underset{1\le i\le n-1}{\max }|c_i^{*}|=|c_s^{*}|$. Z postaci układu otrzymujemy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned |c_s^*| &= 2|c_s^*|-|c_s^*|(u_s+w_s) \,\le\, |u_sc_{s-1}^*+2c_s^*+w_sc_{s+1}| \\ &= |f(x_{s-1},x_s,x_{s+1})|\,\le\, \Big|\frac{f''(\xi_3)}2\Big|\,\le\,\frac 12 M, \endaligned}

a stąd

$|f(x)-s_f(x)|\le 5M{h}_i^2,$

co kończy dowód.

Przykład

Porównanie interpolacji splajnowej i Lagrange'a.

Interpolacja splajnowa wydaje się lepiej spełniać zadanie odtworzenia kształtu funkcji

Jak widać, w przeciwieństwie do wielomianu interpolacyjnego, splajn interpolacyjny praktycznie pokrywa się z wykresem funkcji, tutaj: $f(x)=\frac{1}{1+x^2}$.

Uwaga

Niech

$W_M^r(a,b)=\{f\in W^r(a,b):\underset{a}{\overset{b}{\int }}{(f^{(r)}(x))}^{2}dx\le M\}.$

Ustalmy węzły $a=x_0<\cdots <x_n=b$. Dla $f\in W_M^r(a,b)$, niech $s_f$ będzie naturalną funkcją sklejaną interpolującą $f$ w $x_j$, $0\le j\le n$, a $a_f$ dowolną inną aproksymacją korzystającą jedynie z informacji o wartościach $f$ w tych węzłach, tzn.

$a_f=\varphi (f(x_0),\dots ,f(x_n)).$

Załóżmy, że błąd aproksymacji mierzymy nie w normie Czebyszewa, ale w normie średniokwadratowej zdefiniowanej jako

$\Vert g{\Vert }_{{{ℒ}}_2(a,b)}=\sqrt{\underset{a}{\overset{b}{\int }}(g(x){)}^{2}dx}.$

Wtedy

$\underset{f\in W_M^r(a,b)}{\sup }\Vert f-s_f{\Vert }_{{{ℒ}}_2(a,b)}\le \underset{f\in W_M^r(a,b)}{\sup }\Vert f-a_f{\Vert }_{{{ℒ}}_2(a,b)}.$

Aproksymacja naturalnymi funkcjami sklejanymi jest więc optymalna w klasie $W_M^r(a,b)$.

Można również pokazać, że interpolacja $s_f^{*}$ naturalnymi funkcjami sklejanymi na węzłach równoodległych Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle x_j=a+(b-a)j/ń} , $0\le j\le n$, jest optymalna co do rzędu w klasie $W_M^r(a,b)$, wśród wszystkich aproksymacji korzystających jedynie z informacji o wartościach funkcji w $n+1$ dowolnych punktach, oraz

$\underset{f\in W_M^r(a,b)}{\max }\Vert f-s_f^{*}{\Vert }_{{{ℒ}}_2(a,b)}\asymp n^{-r}.$

Uwaga

Tak jak wielomiany, naturalne funkcje sklejane interpolujące dane funkcje można reprezentować przez ich współczynniki w różnych bazach. Do tego celu można na przykład użyć bazy kanonicznej $K_j$, $0\le j\le n$ zdefiniowanej równościami

$K_j(x_i)=\{\begin{array}{ll}0& i\ne j,\\ 1& i=j,\end{array}$

przy której $s_f(x)=\sum _{j=0}^{n}f(x_j)K_j(x)$. Baza kanoniczna jest jednak niewygodna w użyciu, bo funkcje $K_j$ w ogólności nie zerują się na żadnym podprzedziale, a tym samym manipulowanie nimi jest utrudnione.

Częściej używa się bazy B-sklejanej. Można ją zdefiniować dla splajnów dowolnego rzędu za pomocą wzoru rekurencyjnego (przyjmując, że dla dowolnego $i$, $x_i<x_{i+1}$):

Parser nie mógł rozpoznać (nieznana funkcja „\beginmatrix”): {\displaystyle \displaystyle B_i^0(x) = \left\{ \beginmatrix 1, & \mbox{ jeśli } x_i \leq x < x_{i+1},\\ 0, & \mbox{ w przeciwnym przypadku} ; \endmatrix \right. } Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle B_i^r(x) &= \frac{x-x_i}{x_{i+r}-x_i} B_i^{r-1}(x) + \frac{x_{i+r+1}-x}{x_{i+r+1}-x_{i+1}} B_{i+1}^{r-1}(x). }

W przypadku naturalnych splajnów kubicznych, $r=2$, baza B-sklejana jest jawnie zdefiniowana przez następujące warunki:

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned B_j(x_j) &= 1, \qquad \mbox{ dla } 0\le j\le n, \\ B_j(x) &= 0,\qquad \mbox{ dla } x\le x_{j-2}, j\ge 2, \mbox{ oraz dla } x\ge x_{j+2}, j\le n-2. \endaligned}

Dla $B_0$ i $B_1$ dodatkowo żądamy, aby

${B_0}^{″}(x_0)=0={B_1}^{″}(x_0),B_1(x_0)=0,$

a dla $B_{n-1}$ i $B_n$ podobnie

$B_{n^{″}-1}(x_n)=0={B_n}^{″}(x_n),B_{n-1}(x_{n-1})=0.$

Wtedy $B_j$ nie zeruje się tylko na przedziale $(x_{j-2},x_{j+2})$. Wyznaczenie współczynników rozwinięcia w bazie $\{B_i{\}}_{i=0}^n$ funkcji sklejanej interpolującej $f$ wymaga rozwiązania układu liniowego z macierzą trójdiagonalną $\{B_j(x_i){\}}_{i,j=0}^n$, a więc koszt obliczenia tych współczynników jest proporcjonalny do $n$.

Uwaga

Oprócz naturalnych funkcji sklejanych często rozpatruje się też okresowe funkcje sklejane. Są to funkcje Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle \tilde s:R\toR} spełniające warunki (i), (ii) \link{splinedef}{definicji funkcji sklejanej}, oraz warunek:

(iii)'

${\tilde{s}}^{(i)}$ jest dla $0\le i\le r-1$

funkcją okresową o okresie $(b-a)$, tzn. ${\tilde{s}}^{(i)}(x)={\tilde{s}}^{(i)}(x+(b-a))$, $\mathrm{\forall }x$.

Klasę okresowych funkcji sklejanych rzędu $r$ oznaczymy przez ${\widetilde{{𝒮}}}_r$. Funkcje te mają podobne własności jak naturalne funkcje sklejane. Dokładniej, niech

${\tilde{W}}^r(a,b)=\{f\in W^r(a,b):f^{(i)}(a)=f^{(i)}(b),0\le i\le r-1\},$

tzn. ${\tilde{W}}^r(a,b)$ jest klasą funkcji z $W^r(a,b)$, które można przedłużyć do funkcji, krórych wszystkie pochodne do rzędu $r-1$ włącznie są $(b-a)$-okresowe na $R$. Wtedy dla dowolnej funkcji $f\in {\tilde{W}}^r(a,b)$ zerującej się w węzłach $x_j$, oraz dla dowolnej $\tilde{s}\in {\widetilde{{𝒮}}}_r$ mamy

$\underset{a}{\overset{b}{\int }}{f}^{(r)}(x){\tilde{s}}^{(r)}(x)dx=0.$

Wynika z niego jednoznaczność rozwiązania zadania interpolacyjnego dla okresowych funkcji $f$ (tzn. takich, że $f(a)=f(b)$), jak również odpowiednia własność minimalizacyjna okresowych funkcji sklejanych. Dokładniej, jeśli $f\in {\tilde{W}}^r(a,b)$ oraz ${\tilde{s}}_f\in {\widetilde{{𝒮}}}_r$ interpoluje $f$ w węzłach $x_j$, $0\le j\le n$, to

$\underset{a}{\overset{b}{\int }}(f^{(r)}(x){)}^{2}dx\ge \underset{a}{\overset{b}{\int }}({\tilde{s}}_f^{(r)}(x){)}^{2}dx.$

Dygresja o najlepszej aproksymacji

Klasyczne zadanie aproksymacyjne w przestrzeniach funkcji definiuje się w następujący sposób.

Niech $F$ będzie pewną przestrzenią liniową funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:[a,b]\toR} , w której określona została norma $\Vert \cdot \Vert$. Niech $V_n\subset F$ będzie podprzestrzenią w $F$ wymiaru $n$. Dla danej $f\in F$, należy znaleźć funkcję $v_f\in F$ taką, że

$\Vert f-v_f\Vert =\underset{v\in V_n}{\min }\Vert f-v\Vert .$

Okazuje się, że tak postawione zadanie ma rozwiązanie $v_f$, choć nie zawsze jest ono wyznaczone jednoznacznie.

Jako przykład, rozpatrzmy $F=W^r(a,b)$. Utożsamiając funkcje $f_1,f_2\in W^r(a,b)$ takie, że $f_1(x)-f_2(x)\in {\mathrm{\Pi }}_{r-1}$, zdefiniujemy w $W^r(a,b)$ normę

$\Vert f\Vert =\sqrt{\underset{a}{\overset{b}{\int }}{(f^{(r)}(x))}^{2}dx}.$

Dla ustalonych węzłów $a=x_0<\cdots <x_n=b$, niech

$V_{n+1}={{𝒮}}_r$

będzie podprzestrzenią w $W^r(a,b)$ naturalnych funkcji sklejanych rzędu $r$ opartych węzłach $x_j$, $0\le j\le n$. Oczywiście $\text{dim}{{𝒮}}_r=n+1$, co wynika z jednoznaczności rozwiązania w ${{𝒮}}_r$ zadania interpolacji. Okazuje się, że wtedy optymalną dla $f\in W^r(a,b)$ jest naturalna funkcja sklejana $s_f$ interpolująca $f$ w węzłach $x_j$, tzn.

$\Vert f-s_f\Vert =\underset{s\in {{𝒮}}_r}{\min }\Vert f-s\Vert .$

Rzeczywiście, ponieważ norma w przestrzeni $W^r(a,b)$ generowana jest przez iloczyn skalarny

$(f_1,f_2)=\underset{a}{\overset{b}{\int }}{f}_1^{(r)}(x)f_2^{(r)}(x)dx,$

jest to przestrzeń unitarna. Znane twierdzenie mówi, że w przestrzeni unitarnej najbliższą danej $f$ funkcją w dowolnej domkniętej podprzestrzeni $V$ jest rzut prostopadły $f$ na $V$, albo równoważnie, taka funkcja $v_f\in V_{n+1}$, że iloczyn skalarny

$(f-v_f,v)=0,\mathrm{\forall }v\in V.$

W naszym przypadku, ostatnia równość jest równoważna

$\underset{a}{\overset{b}{\int }}(f-v_f{)}^{(r)}(x)s^{(r)}(x)dx=0,\mathrm{\forall }s\in {{𝒮}}_r.$

To zaś jest prawdą, gdy $v_f$ interpoluje $f$ w punktach $x_j$, czyli $v_f=s_f$.

Dodajmy jeszcze, że nie zawsze interpolacja daje najlepszą aproksymację w sensie klasycznym.

Literatura

W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj rozdział 6.4 w

• D. Kincaid, W. Cheney Analiza numeryczna, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X.

Warto także zapoznać się (nieobowiązkowo) z rozdziałami 6.5 i 6.6 tamże.