Układy elektroniczne i technika pomiarowa/Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
| Linia 158: | Linia 158: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd20.png]] | ||
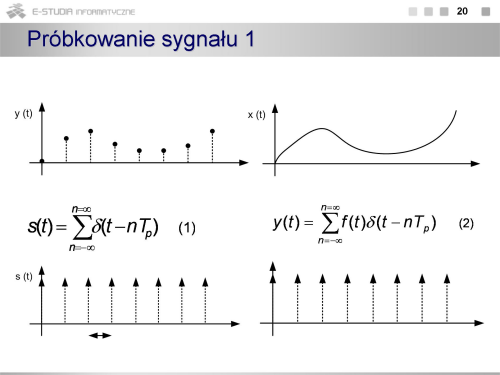
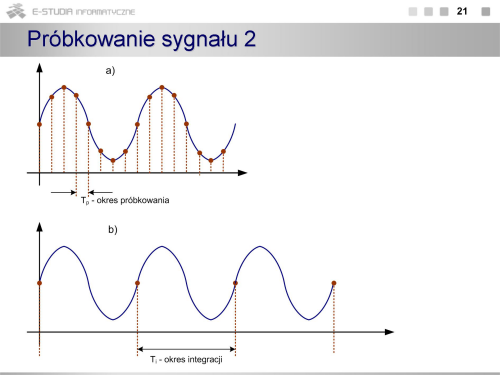
|valign="top"| | |valign="top"|Próbkowanie polega na rejestracji wartości sygnału z odstępem czasowym określanym jako okres próbkowania. Problem próbkowania od strony teoretycznej jest rozważany w ramach wykładu z Teorii Sygnałów. Elementarnym zagadnieniem jest tutaj kwestia dopasowania częstotliwości próbkowania do pasma przetwarzanych sygnałów. Z twierdzenia Nyquista, opisanego zależnością (1) wynika, że aby można było odtworzyć sygnał z jego próbek bez zniekształceń, częstotliwość próbkowania musi być przynajmniej 2 razy większa od częstotliwości najwyższej harmonicznej występującej w sygnale. W rzeczywistości sygnały pomiarowe rzadko mają ograniczone pasmo, a ponadto częstotliwość maksymalna musiałaby być znana przed rozpoczęciem procesu przetwarzania. Stąd spełnienie warunku (1) wymaga zastosowania dodatkowego układu wejściowego tzw. filtru antyaliasingowego. W praktyce relacja pomiędzy częstotliwością próbkowania, a częstotliwością sygnału zależy zarówno od celu przetwarzania (pomiar parametrów, rejestracja, analiza widmowa) jak i charakteru zmienności sygnału (ciągły sygnał okresowy, przebieg jednokrotny, sygnał logiczny). Inne zatem będą warunki próbkowania w multimetrach, oscyloskopach cyfrowych, analizatorach widma czy analizatorach stanów logicznych. Proces próbkowania może być realizowany zarówno przez sam przetwornik analogowo-cyfrowy jak i przez specjalny układ próbkująco-pamiętający (S/H). Układy scalone, realizujące przetwarzanie analogowo-cyfrowe, często zawierają w swojej strukturze układ S/H i właściwy przetwornik a/c. | ||
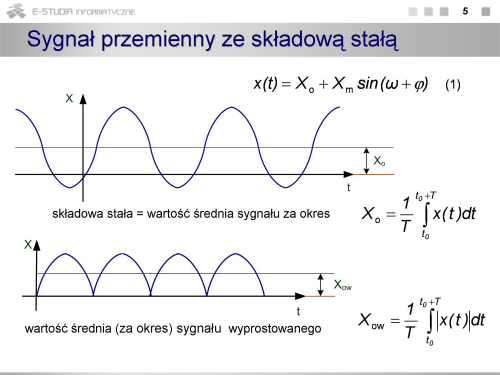
Na rys. (b) pokazano przetwarzanie, którego celem nie jest wyznaczenie chwilowych wartości sygnału, ale wartości średniej w pewnym przedziale czasowym określanym jako czas integracji. W odniesieniu do przetworników a/c rysunek sygnalizuje podstawowy podział tych przetworników na układy przetwarzające wartość chwilową i wartość średnią. | |||
|} | |} | ||
| Linia 165: | Linia 167: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd21.png]] | ||
|valign="top"| | |valign="top"|Matematycznie próbkowanie można interpretować jak mnożenie sygnału ciągłego x(t) przez funkcję próbkującą s(t) w postaci impulsów Diraca (1). | ||
|} | |} | ||
| Linia 172: | Linia 174: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd22.png]] | ||
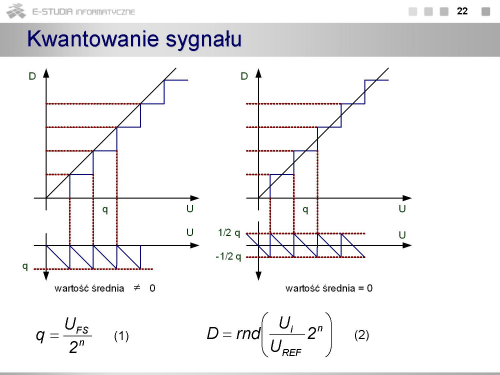
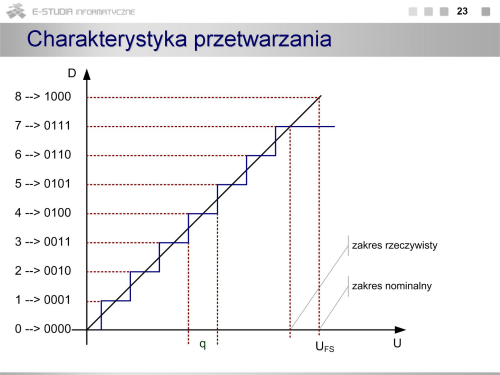
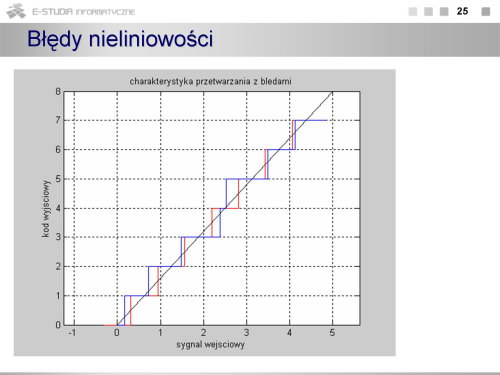
|valign="top"| | |valign="top"|Kwantowanie sygnału polega na przyporządkowaniu ciągłym przedziałom wartości sygnału analogowego pewnych wartości dyskretnych w postaci cyfrowej. Nieuchronnie następuje przy tym strata informacji, ponieważ nieskończonej liczbie wartości sygnału w każdym przedziale jest przypisana tylko jedna wartość cyfrowa. Odwzorowanie ciągłych wartości sygnału analogowego (w praktyce napięcia) na cyfrowe będzie tym dokładniejsze im przedział wartości analogowych będzie mniejszy. Ten elementarny przedział jest określany jako przedział kwantowania i opisany jako q (UFS jest pełnym zakresem przetwarzania, a n liczbą bitów przetwornika). | ||
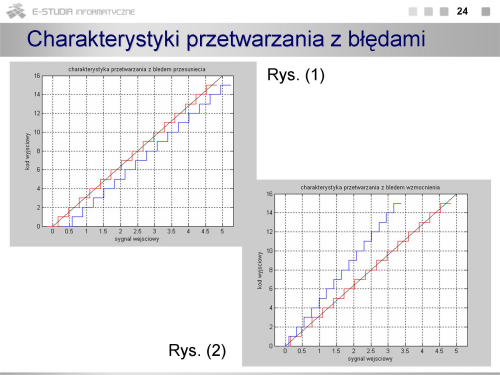
Matematycznie proces kwantowania (czasami również całego przetwarzania a/c) jest opisany równaniem (2), gdzie Ui – napięcie wejściowe, UREF – napięcie odniesienia określające zakres przetwarzania. Na rysunkach pokazano charakterystykę przejściową unipolarnego przetwornika a/c (o dodatniej polaryzacji napięcia wejściowego). Charakterystyka ma postać przebiegu schodkowego. Na rysunku pokazano również fragment teoretycznej (o nieskończenie małym przedziale kwantowania) charakterystyki przetwarzania łączącej punkt o współrzędnych [0V, najmniejszy co do wartości bezwzględnej stan przetwornika] z punktem o współrzędnych [UFS , maksymalny stan przetwornika]. Taki opis charakterystyki wynika z stąd, że przetwornik może działać w dowolnym kodzie i niekoniecznie najmniejszy stan przetwornika musi oznaczać, że wszystkie bity są równe 0. Poniżej charakterystyki przejściowej pokazano jak zmienia się błąd kwantowania stanowiący różnicę pomiędzy wartościami rzeczywistymi z charakterystyki schodkowej, a wartościami z idealnej charakterystyki przetwarzania. Z rysunku widać, że charakterystyka rzeczywista znajduje się zawsze poniżej charakterystyki idealnej, a błąd kwantowania zmienia się od 0 do q. Wartość średnia tego błędu jest różna od zera. Dodatkowy problem stanowi przejście przez 0, gdyby taki przetwornik miał pracować jako bipolarny (powstaje nieciągłość lub charakterystyka w ogóle nie przechodzi przez 0). | |||
Charakterystykę przejściową kształtuje się (tak jak na rysunku) przez przemieszczenie jej o wartość odpowiadającą ½ q. Wówczas wartość średnia błędu kwantowania wynosi 0, a charakterystyka dla przetwornika bipolarnego ma przebieg monotoniczny. | |||
|} | |} | ||
Wersja z 16:54, 28 wrz 2006
wersja beta
Moduł 10 - Przetwarzanie wielkości elektrycznych

|

|
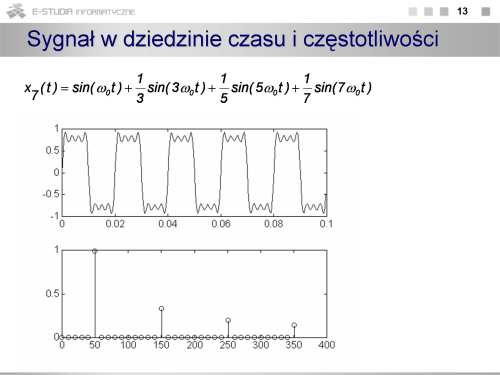
Sygnały pomiarowe
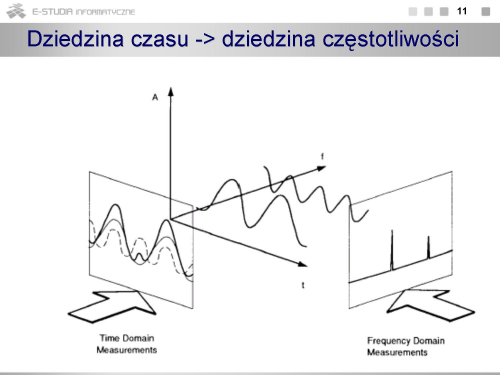
|
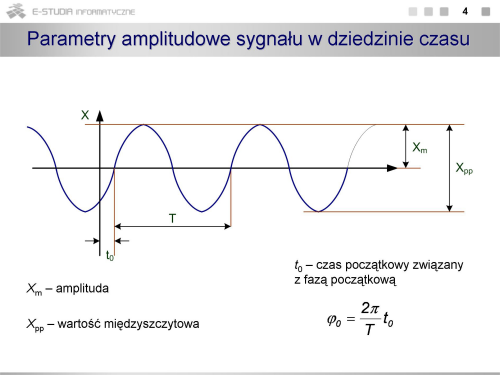
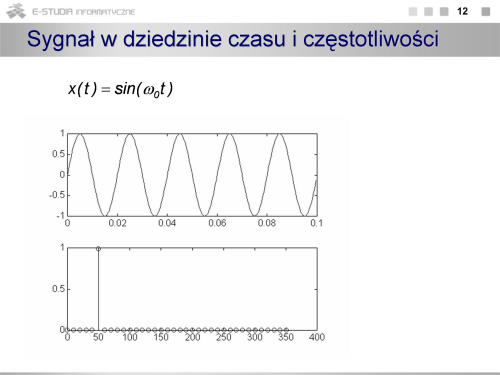
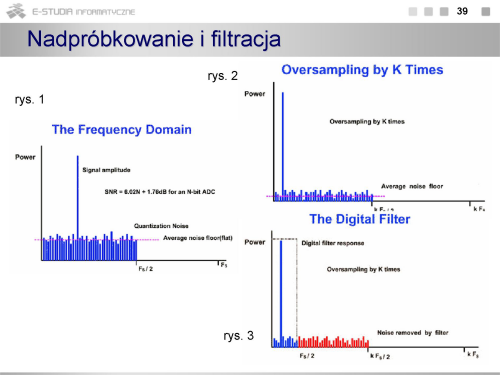
Na rysunku przedstawiono poglądowo obraz sygnału w dziedzinie częstotliwości. Stanowią go prążki o wysokości odpowiadającej wartości harmonicznych. |
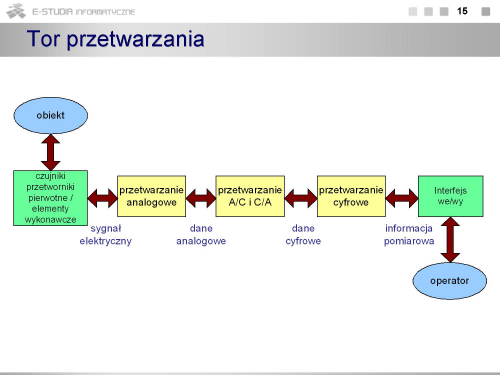
Tor przetwarzania sygnałów
Przetwarzanie analogowo-cyfrowe
|
Matematycznie próbkowanie można interpretować jak mnożenie sygnału ciągłego x(t) przez funkcję próbkującą s(t) w postaci impulsów Diraca (1). |
|
|
|

|

|
|

|
|
|
|
|

|
|

|
|

|
|
|