Układy elektroniczne i technika pomiarowa/Moduł 2

wersja beta

---

Moduł 2 - Sprzężenie zwrotne

Wykład 2. Sprzężenie zwrotne

---

Wstęp Koncepcję sprzężenia zwrotnego, w latach trzydziestych dwudziestego wieku, opublikował H. S. Black i obecnie jest ono (sprzężenie zwrotne) powszechnie stosowne w analogowych układach elektronicznych. W niniejszym module opisano podstawowe elementy teorii sprzężenia zwrotnego. Wprowadzono klasyfikację sprzężeń zwrotnych oraz omówiono podstawowe pojęcia związane z opisem sygnałów i ich transmisją w analogowych układach elektronicznych. Przedstawiono także wpływ sprzężenia zwrotnego na podstawowe parametry układu elektronicznego, takie jak: wzmocnienie, impedancję wejściową i wyjściową, charakterystyki częstotliwościowe, zakłócenia i szumy oraz stabilność i liniowość.

---

Słowniczek sprzężenie zwrotne – transmisja całego lub części sygnału wyjściowego w układzie elektronicznym i po zsumowaniu z sygnałem sterującym ponowne zadanie go na wejście układu stopień sprzężenia zwrotnego lub współczynnik redukcji wzmocnienia – wyrażenie, jeden minus wzmocnienie pętli sprzężenia zwrotnego, występujące w mianowniku transmitancji układu zamkniętego

---

sygnał sprzężenia zwrotnego – sygnał wyjściowy czwórnika sprzężenia zwrotnego, który jest sumowany z sygnałem sterującym układ elektroniczny transmitancja czwórnika sprzężenia zwrotnego – transmitancja widmowa układu liniowego, szczególny przypadek transmitancji operatorowej układu liniowego. Jest to stosunek sygnałów harmonicznych wyjściowego do wejściowego czwórnika sprzężenia zwrotnego zapisanych w postaci liczb zespolonych transmitancja układu otwartego - transmitancja widmowa układu liniowego, szczególny przypadek transmitancji operatorowej układu liniowego. Jest to stosunek sygnałów harmonicznych wyjściowego do wejściowego układu elektronicznego ( np. wzmacniacza) zapisanych w postaci liczb zespolonych

---

układ regulacji automatycznej – układ sterowania, w którym zastosowano sprzężenie zwrotne, układ zamknięty układ zamknięty – układ ze sprzężeniem zwrotnym wzmocnienie pętli sprzężenia zwrotnego – moduł iloczynu transmitancji widmowej układu otwartego i transmitancji widmowej czwórnika sprzężenia zwrotnego

---

Pojęcia podstawowe Termin sprzężenie zwrotne jest związany z teorią transmisji sygnałów i oznacza, że napięcie wyjściowe dowolnego liniowego układu analogowego, np. wzmacniacza akustycznego, w odpowiedniej proporcji oraz w miarę potrzeby odpowiednio odfiltrowane ponownie jest kierowane do wejścia wzmacniacza i dodaje się lub odejmuje się od sygnału sterującego. Kiedy sygnał sprzężenia zwrotnego odejmuje się od sygnału sterującego wzmacniacz, występuje sprzężenie zwrotne ujemne. Jeżeli sygnały sterujący i sprzężenia zwrotnego dodają się, występuje sprzężenie zwrotne dodatnie.

---

Podobnie jak w układach regulacji automatycznej gdzie bloki są opisane transmitancją widmową tak i poszczególne fragmenty lub całe układy elektroniczne można traktować jak czwórniki i także można je opisać odpowiednią transmitancją widmową np. $K(j\omega ),\beta (j\omega )$.

---

---

Weźmy pod uwagę schemat blokowy układu przedstawiony na rysunku. Układ składa się z dwóch czwórników o transmitancjach: $K(j\omega )$ – dla czwórnika wzmacniacza, $\beta (j\omega )$ – dla czwórnika sprzężenia zwrotnego. Ponieważ w ogólnym wypadku transmitancje widmowe obu czwórników zależą od częstotliwości dlatego są funkcjami zmiennych zespolonych. Transmitancję widmową $K(j\omega )$ nazywamy transmitancją układu otwartego, a transmitancję widmową $\beta (j\omega )$ transmitancją czwórnika sprzężenia zwrotnego. Przyjmując oznaczenia: $X(j\omega )$ – sygnał sterujący, $X_s(j\omega )$ – sygnał wyjściowy czwórnika sprzężenia zwrotnego, $X_i(j\omega )$ – sygnał wejściowy czwórnika wzmacniacza, $Y(j\omega )$ – sygnał wyjściowy, który jest jednocześnie sygnałem wejściowym czwórnika sprzężenia zwrotnego, przedstawiony na rysunku schemat można opisać równaniami: $K(j\omega )=\frac{Y(j\omega )}{X_i(j\omega )}$ 2.1 $\beta (j\omega )=\frac{X_s(j\omega )}{Y(j\omega )}$ 2.2 Łatwo zauważyć, że dla sprzężenia zwrotnego ujemnego $X(j\omega )-X_s(j\omega )=X_i(j\omega )$ 2.3 a dla sprzężenia zwrotnego dodatniego $X(j\omega )+X_s(j\omega )=X_i(j\omega )$ 2.4

---

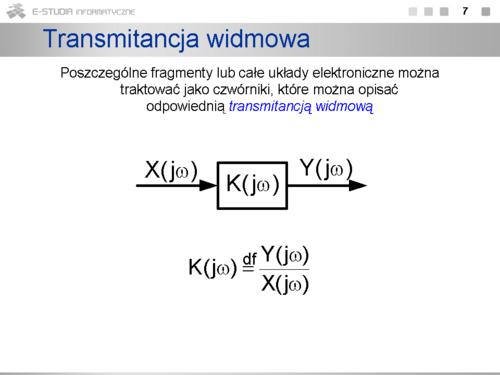
Transmitancja układu ze sprzężeniem zwrotnym $K_z(j\omega )$, zwanego krótko układem zamkniętym, uwzględniając zależności 2.1, 2.2, oraz 2.3. lub 2.4, jest opisana zależnością: Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle K_z(j\omega)= \frac{Y(j\omega)}{X(j\omega)}=\frac{K(j\omega)}{1-K(j\omega)\cdot \beta(j\omega)}}} 2.5 Ponieważ czwórnik sprzężenia zwrotnego najczęściej spełnia zależność $\beta (j\omega )>0$ (sprzężenie nie odwraca fazy sygnału), aby zrealizować ujemne sprzężenie zwrotne, czwórnik wzmacniacza powinien spełnić zależność $K(j\omega )<0$ (odwraca fazę), a dla sprzężenia zwrotnego dodatniego $K(j\omega )>0$ (nie odwraca fazy).

---

Iloczyn $|K(j\omega )\cdot \beta (j\omega )|$ jest nazywany wzmocnieniem pętli sprzężenia zwrotnego. Jeżeli wzmocnienie pętli jest duże mówimy, że w układzie zastosowano silne sprzężenie zwrotne. Dołączenie czwórnika sprzężenia zwrotnego zmienia wzmocnienie układu otwartego. W zależności od warunku jaki spełnia wyrażenie $1-K(j\omega )\cdot \beta (j\omega )$ można wyróżnić trzy podstawowe skutki działania sprzężenia zwrotnego:

---

$\begin{array}{ccc}Przypadek1.& |1-K(j\omega )\cdot \beta (j\omega )|>1;& |K_z(j\omega )|<|K(j\omega )|\end{array}$ 2.6 W układzie występuje ujemne sprzężenie zwrotne. Wzmocnienia w układzie zamkniętym w stosunku do wzmocnienia jakie było w układzie otwartym zmniejsza się.

---

$\begin{array}{ccc}Przypadek2.& |1-K(j\omega )\cdot \beta (j\omega )|>1;& |K_z(j\omega )|>|K(j\omega )|\end{array}$ 2.7 W układzie występuje dodatnie sprzężenie zwrotne, które powoduje w układzie zamkniętym zwiększenie wzmocnienia w stosunku do wzmocnienia jakie było w układzie otwartym.

---

$\begin{array}{ccc}Przypadek3.& |1-K(j\omega )\cdot \beta (j\omega )|=0;& |K_z(j\omega )|\to \mathrm{\infty }\end{array}$ 2.8 Dodatnie sprzężenie zwrotne jest tak silne, że możliwa jest praca układu zamkniętego bez zewnętrznego sygnału sterującego. W układach elektronicznych wykorzystuje się wszystkie trzy wyżej wymienione przypadki. Pierwszy jest stosowany we wzmacniaczach głównie w celu poprawy ich parametrów eksploatacyjnych. W przypadku układów ze wzmacniaczami operacyjnymi wzmocnieniem pętli sprzężenia zwrotnego jest bardzo duże. Oznacza to, że oddziaływanie pętli sprzężenia zwrotnego jest tak silne, że o właściwościach statycznych i dynamicznych układu zamkniętego decydują wyłącznie elementy z jakich jest zbudowana pętla sprzężenia zwrotnego. Do budowy tej pętli stosuje się elementy pasywne (np. kondensator i rezystory) o stabilnych parametrach nie wrażliwych np. na zmianę temperatury. Drugi przypadek jest powszechnie stosowany w układach przełączających, głównie w technice cyfrowej, w których pętla sprzężenia zwrotnego działa forsująco, powodując szybką zmianę stanu łączników elektronicznych. Umożliwia to uzyskanie sygnałów impulsowych o dużej stromości narastania i opadania. Trzeci przypadek występuje w układach generatorów drgań sinusoidalnych z pętlą sprzężenia zwrotnego.

---

Klasyfikacja sprzężeń zwrotnych Podstawowy podział sprzężeń zwrotnych to podział na sprzężenie zwrotne dodatnie i sprzężenie zwrotne ujemne. Tę cechę należy bezwzględnie podać, aby ocenić właściwości układu z punktu widzenia transmisji i przetwarzania sygnałów. Ponad to sprzężenia zwrotne dzielimy: ze względu na sposób wprowadzenia sygnału sprzężenia zwrotnego na wejście wzmacniacza na sprzężenie zwrotne szeregowe i sprzężenie zwrotne równoległe, ze względu na sposób próbkowania (pomiaru) sygnału sprzężenia zwrotnego na wyjściu wzmacniacza na sprzężenie zwrotne prądowe i sprzężenie zwrotne napięciowe, ze względu na kształt charakterystyki częstotliwościowej czwórnika sprzężenia zwrotnego na sprzężenie zwrotne selektywne i sprzężenie zwrotne liniowe (nieselektywne). ze względu na liczbę czwórników (stopni wzmacniających) w torze wzmacniacza na sprzężenie zwrotne jednostopniowe i sprzężenie zwrotne wielostopniowe, ze względu na rodzaj zastosowanych do budowy pętli sprzężenia zwrotnego elementów na sprzężenie zwrotne pasywne i sprzężenie zwrotne aktywne.

---

Sprzężenie zwrotne: a) szeregowe, b) równoległe c) napięciowe, d) prądowe Te cechy sprzężenia zwrotnego (szeregowe czy równoległe, napięciowe czy prądowe) należy bezwzględnie podać, jeżeli chcemy dokładnie określić, z punktu widzenia transmisji sygnałów, rodzaj zastosowanego w układzie sprzężenia zwrotnego i jednoznacznie opisać skutki jego zastosowania.

---

Przykłady realizacji rzeczywistych układów ze sprzężeniem zwrotnym. Proste przykłady zastosowania ujemnego sprzężenia zwrotnego: a) sprzężenie napięciowe-równoległe, b) sprzężenie prądowe-szeregowe.

---

W zależności od rodzaju zastosowanego sprzężenia zwrotnego poszczególne transmitancje widmowe $K(j\omega )$ i $\beta (j\omega )$ maja różną postać, stosownie do tego, jakie sygnały są rozważane na wejściu i na wyjściu układu. Dla sprzężenia napięciowego-szeregowego $\begin{array}{cc}K(j\omega )=\frac{U(j\omega )}{U_i(j\omega )}=K_u(j\omega );& \beta (j\omega )=\frac{U_s(j\omega )}{U(j\omega )}={\beta }_u(j\omega )\end{array}$ 2.9 Dla sprzężenia napięciowego-równoległego $\begin{array}{cc}K(j\omega )=\frac{U(j\omega )}{I_i(j\omega )}=K_{ui}(j\omega );& \beta (j\omega )=\frac{I_s(j\omega )}{U(j\omega )}={\beta }_{iu}(j\omega )\end{array}$ 2.10 Dla sprzężenia prądowego-szeregowego $\begin{array}{cc}K(j\omega )=\frac{I(j\omega )}{U_i(j\omega )}=K_{iu}(j\omega );& \beta (j\omega )=\frac{U_s(j\omega )}{I(j\omega )}={\beta }_{ui}(j\omega )\end{array}$ 2.11 Dla sprzężenia prądowego-równoległego $\begin{array}{cc}K(j\omega )=\frac{I(j\omega )}{I_i(j\omega )}=K_i(j\omega );& \beta (j\omega )=\frac{I_s(j\omega )}{I(j\omega )}={\beta }_i(j\omega )\end{array}$ 2.12

---

---

---

---

---

---

---

---