Układy elektroniczne i technika pomiarowa/Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 90: | Linia 90: | ||
Ponieważ w ogólnym wypadku transmitancje widmowe obu czwórników zależą od częstotliwości dlatego są funkcjami zmiennych zespolonych. | Ponieważ w ogólnym wypadku transmitancje widmowe obu czwórników zależą od częstotliwości dlatego są funkcjami zmiennych zespolonych. | ||
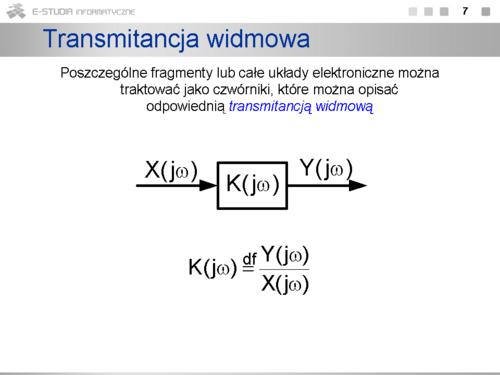
Transmitancję widmową <math>K(j\omega)\,</math> nazywamy transmitancją układu otwartego, a | Transmitancję widmową <math>K(j\omega)\,</math> nazywamy ''transmitancją układu otwartego'', a | ||
transmitancję widmową <math>\beta(j\omega)\,</math> transmitancją czwórnika sprzężenia zwrotnego. | transmitancję widmową <math>\beta(j\omega)\,</math> ''transmitancją czwórnika sprzężenia zwrotnego''. | ||
Przyjmując oznaczenia: | Przyjmując oznaczenia: | ||
| Linia 105: | Linia 105: | ||
:{| width="100%" | :{| width="100%" | ||
| width="95%" align="left" | <math>\displaystyle K(j\omega)=\frac{Y(j\omega)}{X_i(j\omega)}</math> | | width="95%" align="left" | <math>\displaystyle K(j\omega)=\frac{Y(j\omega)}{X_i(j\omega)}</math> | ||
| align="right" | '' | | align="right" | ''2.1'' | ||
|} | |} | ||
:{| width="100%" | :{| width="100%" | ||
| width="95%" align="left" | <math>\displaystyle \beta(j\omega)=\frac{X_s(j\omega)}{Y(j\omega)}</math> | | width="95%" align="left" | <math>\displaystyle \beta(j\omega)=\frac{X_s(j\omega)}{Y(j\omega)}</math> | ||
| align="right" | '' | | align="right" | ''2.2'' | ||
|} | |} | ||
| Linia 117: | Linia 117: | ||
:{| width="100%" | :{| width="100%" | ||
| width="95%" align="left" | <math>\displaystyle X(j\omega)-X_s(j\omega)= X_i(j\omega)</math> | | width="95%" align="left" | <math>\displaystyle X(j\omega)-X_s(j\omega)= X_i(j\omega)</math> | ||
| align="right" | '' | | align="right" | ''2.3'' | ||
|} | |} | ||
| Linia 124: | Linia 124: | ||
:{| width="100%" | :{| width="100%" | ||
| width="95%" align="left" | <math>\displaystyle X(j\omega)+X_s(j\omega)= X_i(j\omega)</math> | | width="95%" align="left" | <math>\displaystyle X(j\omega)+X_s(j\omega)= X_i(j\omega)</math> | ||
| align="right" | '' | | align="right" | ''2.4'' | ||
|} | |} | ||
| Linia 133: | Linia 133: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M2_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M2_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Transmitancja układu ze sprzężeniem zwrotnym <math>K_z(j\omega)\,</math>, zwanego krótko ''układem zamkniętym'', uwzględniając zależności 2.1, 2.2, oraz 2.3. lub 2.4, jest opisana zależnością: | ||
:{| width="100%" | |||
| width="95%" align="left" | <math>\displaystyle K_z(j\omega) \frac{Y(j\omega)}{X(j\omega)}=\frac{K(j\omega}{1-K(j\omega}\cdot \beta(j\omega</math> | |||
| align="right" | ''2.5'' | |||
|} | |||
Ponieważ czwórnik sprzężenia zwrotnego najczęściej spełnia zależność <math>\beta(j\omega)>0\,</math> (sprzężenie nie odwraca fazy sygnału), aby zrealizować ujemne sprzężenie zwrotne, czwórnik wzmacniacza powinien spełnić zależność <math>K(j\omega)<0\,</math> (odwraca fazę), a dla sprzężenia zwrotnego dodatniego <math>K(j\omega)>0\,</math> (nie odwraca fazy). | |||
|} | |} | ||
---- | ---- | ||
| Linia 139: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M2_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M2_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Iloczyn <math>|K(j\omega)\cdot \beta(jω)|\,</math> jest nazywany '''wzmocnieniem pętli sprzężenia zwrotnego.''' Jeżeli wzmocnienie pętli jest duże mówimy, że w układzie zastosowano silne sprzężenie zwrotne. | ||
Dołączenie czwórnika sprzężenia zwrotnego zmienia wzmocnienie układu otwartego. | |||
W zależności od warunku jaki spełnia wyrażenie <math>1-K(j\omega)\cdot \beta(j\omega)\,</math> można wyróżnić trzy podstawowe skutki działania sprzężenia zwrotnego: | |||
|} | |} | ||
---- | ---- | ||
Wersja z 12:09, 28 wrz 2006
wersja beta
UKŁADY ELEKTRONICZNE I TECHNIKA POMIAROWA
Moduł 2 - Sprzężenie zwrotne
 |
Wykład 2. Sprzężenie zwrotne |
 |
 |
Transmitancja układu ze sprzężeniem zwrotnym , zwanego krótko układem zamkniętym, uwzględniając zależności 2.1, 2.2, oraz 2.3. lub 2.4, jest opisana zależnością:
Ponieważ czwórnik sprzężenia zwrotnego najczęściej spełnia zależność (sprzężenie nie odwraca fazy sygnału), aby zrealizować ujemne sprzężenie zwrotne, czwórnik wzmacniacza powinien spełnić zależność (odwraca fazę), a dla sprzężenia zwrotnego dodatniego (nie odwraca fazy). |
 |
Iloczyn Parser nie mógł rozpoznać (błąd składni): {\displaystyle |K(j\omega)\cdot \beta(jω)|\,}
jest nazywany wzmocnieniem pętli sprzężenia zwrotnego. Jeżeli wzmocnienie pętli jest duże mówimy, że w układzie zastosowano silne sprzężenie zwrotne.
Dołączenie czwórnika sprzężenia zwrotnego zmienia wzmocnienie układu otwartego. W zależności od warunku jaki spełnia wyrażenie można wyróżnić trzy podstawowe skutki działania sprzężenia zwrotnego: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |