|
|
| Linia 91: |
Linia 91: |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd15.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd15.png|thumb|500px]] |
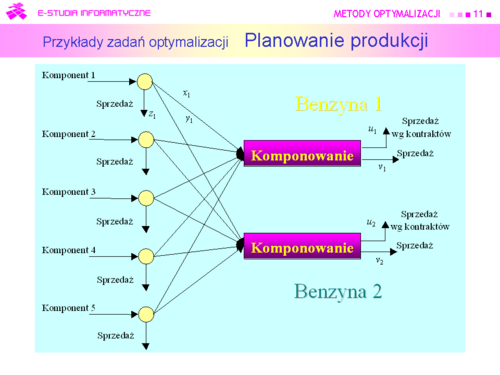
| |valign="top"|We wzorze określającym zysk: | | |valign="top"|We wzorze określającym zysk: |
| <math>p^u_j</math> – cena jednostki j-tej benzyny w kontrakcie, | | <math>p^u_j</math> – cena jednostki ''j''-tej benzyny w kontrakcie, |
|
| |
|
| <math>p^v_j</math> – cena jednostki j-tej benzyny w wolnej sprzedaży, | | <math>p^v_j</math> – cena jednostki ''j''-tej benzyny w wolnej sprzedaży, |
|
| |
|
| <math>p^z_i</math> – cena jednostki i-tego komponentu w wolnej sprzedaży, | | <math>p^z_i</math> – cena jednostki ''i''-tego komponentu w wolnej sprzedaży, |
|
| |
|
| <math>c^s_i</math> – koszt wytworzenia jednostki komponentu i, | | <math>c^s_i</math> – koszt wytworzenia jednostki komponentu ''i'', |
|
| |
|
| <math>c^b_i</math> – koszty komponowania przeliczone na jednostkę komponentu i. | | <math>c^b_i</math> – koszty komponowania przeliczone na jednostkę komponentu ''i''. |
|
| |
|
| |} | | |} |
| Linia 299: |
Linia 299: |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] |
| |valign="top"|Przypadku | | |valign="top"|Przypadku |
| <math>x_i^– = -\infty albo x_i^+ = \infty,</math> | | <math>x_i^- = -\infty albo x_i^+ = \infty</math>, |
| nie wykluczamy | | nie wykluczamy |
|
| |
|
| Linia 519: |
Linia 519: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd84.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd84.png|thumb|500px]] |
| |valign="top"|Jest to funkcja <math>n\cdot m + n +n\cdot m = n(2m + 1)</math> zmiennych. Przy czterech miejscach lokalizacji, n = 4, i dwudziestu pięciu odbiorcach, m = 25, daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego bo trzeba uwzględnić różne produkty a także różne ich rodzaje), jest to niewiele. | | |valign="top"|Jest to funkcja <math>n\cdot m + n +n\cdot m = n(2m + 1)</math> zmiennych. Przy czterech miejscach lokalizacji, ''n'' = 4, i dwudziestu pięciu odbiorcach, ''m'' = 25, daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego bo trzeba uwzględnić różne produkty a także różne ich rodzaje), jest to niewiele. |
| |} | | |} |
| ---- | | ---- |
| Linia 525: |
Linia 525: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd85.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd85.png|thumb|500px]] |
| |valign="top"|Ograniczenia (85.C) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu i nie zostanie wybudowana nowa fabryka to, <math>y_i = 0</math>, zatem na mocy (85.A) i (85.B), dla każdego j wielkość przewozu <math>x_i_j = 0</math>. | | |valign="top"|Ograniczenia (85.C) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu i nie zostanie wybudowana nowa fabryka to, <math>y_i = 0</math>, zatem na mocy (85.A) i (85.B), dla każdego ''j'' wielkość przewozu <math>x_i_j = 0</math>. |
| |} | | |} |
| ---- | | ---- |