|
|
| Linia 92: |
Linia 92: |
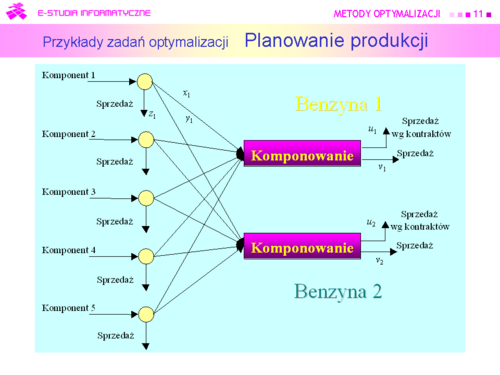
| |valign="top"|We wzorze określającym zysk: | | |valign="top"|We wzorze określającym zysk: |
| <math>p^u_j</math> – cena jednostki j-tej benzyny w kontrakcie, | | <math>p^u_j</math> – cena jednostki j-tej benzyny w kontrakcie, |
| | |
| <math>p^v_j</math> – cena jednostki j-tej benzyny w wolnej sprzedaży, | | <math>p^v_j</math> – cena jednostki j-tej benzyny w wolnej sprzedaży, |
| | |
| <math>p^z_i</math> – cena jednostki i-tego komponentu w wolnej sprzedaży, | | <math>p^z_i</math> – cena jednostki i-tego komponentu w wolnej sprzedaży, |
| | |
| <math>c^s_i</math> – koszt wytworzenia jednostki komponentu i, | | <math>c^s_i</math> – koszt wytworzenia jednostki komponentu i, |
| | |
| <math>c^b_i</math> – koszty komponowania przeliczone na jednostkę komponentu i. | | <math>c^b_i</math> – koszty komponowania przeliczone na jednostkę komponentu i. |
|
| |
|
| Linia 120: |
Linia 124: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] |
| |valign="top"|Współczynniki<math> \eta i i \mu j</math> można traktować dla benzyn np. jako liczbę oktanową. | | |valign="top"|Współczynniki<math> \eta \i \ i \mu j</math> można traktować dla benzyn np. jako liczbę oktanową. |
| |} | | |} |
| ---- | | ---- |
| Linia 156: |
Linia 160: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd25.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd25.png|thumb|500px]] |
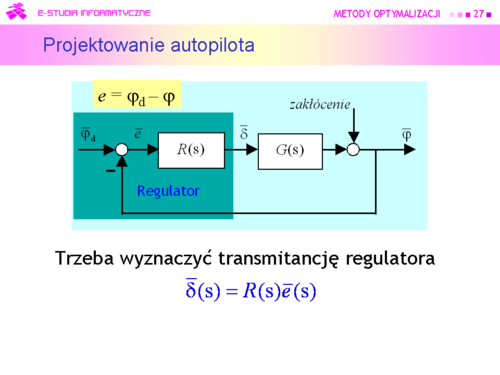
| |valign="top"|Automatycy przy projektowaniu układów sterowania zamiast „opisem różniczkowym” obiektu liniowego wolą posługiwać się równoważnym opisem transmitancyjnym przyjmując, że funkcja <math>\omega(\cdot)</math> będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący <math>\delta(\cdot)</math> mają transformaty Laplace’a. | | |valign="top"|Automatycy przy projektowaniu układów sterowania zamiast „opisem różniczkowym” obiektu liniowego wolą posługiwać się równoważnym opisem transmitancyjnym przyjmując, że funkcja <math>\varphi(\cdot)</math> będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący <math>\delta(\cdot)</math> mają transformaty Laplace’a. |
| |} | | |} |
| ---- | | ---- |