PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 327: | Linia 327: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd25.png|thumb|500px]] | ||
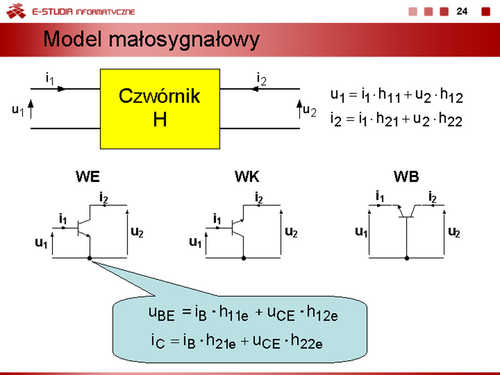
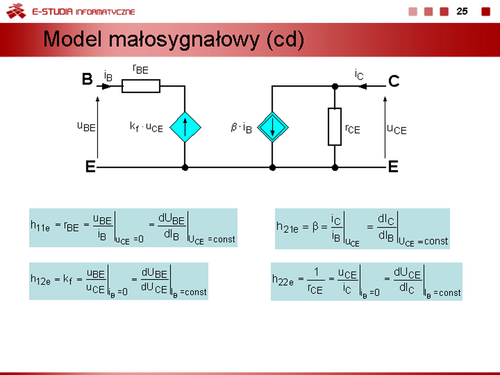
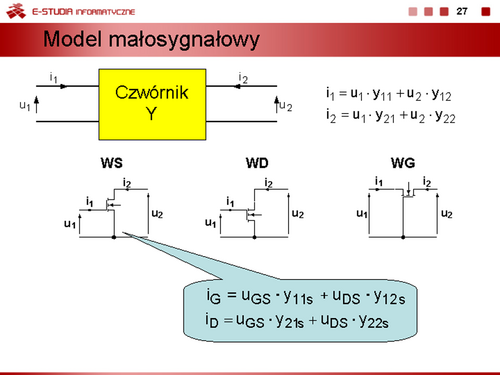
|valign="top"| | |valign="top"|Parametry hybrydowe tej macierzy często nazywane parametrami uniwersalnymi są definiowane następująco | ||
<math>\displaystyle h_{11e}=r_{BE}=\frac{u_{BE}}{i_B}\bigg|_{u_{CE}=0}=\frac{dU_{BE}}{dI_B}\bigg|_{U_{CE}=const}</math> | |||
dynamiczna rezystancja wejściowa w stanie zwarcia na wyjściu, | |||
<math>\displaystyle h_{12e}=k_f=\frac{u_{BE}}{u_{CE}}\bigg|_{i_B=0}=\frac{dU_{BE}}{dU_{CE}}\bigg|_{I_B=const}</math> | |||
współczynnik oddziaływania wstecznego w stanie rozwarcia na wejściu, | |||
<math>\displaystyle h_{21e}=\beta=\frac{i_C}{i_B}\bigg|_{u_{CE=0}}=\frac{dI_C}{dI_B}\bigg|_{U_{CE}=const}</math> | |||
małosygnałowy współczynnik wzmocnienia prądowego w stanie zwarcia na wyjściu, | |||
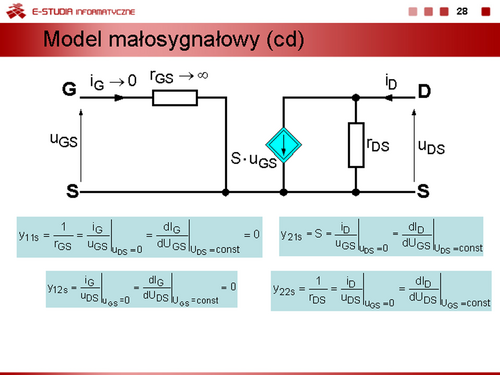
<math>\displaystyle h_{22e}=\frac{1}{r_{CE}}=\frac{u_{CE}}{i_C}\bigg|_{i_B=0}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}</math> | |||
dynamiczna konduktancja (rezystancja) wyjściowa w stanie rozwarcia na wejściu. Schemat zastępczy tranzystora bipolarnego, w którym zastosowano parametry uniwersalne przedstawiono na slajdzie. | |||
|} | |} | ||
Wersja z 03:02, 13 wrz 2006
 |
Wykład 13. Modele elementów półprzewodnikowych |
 |
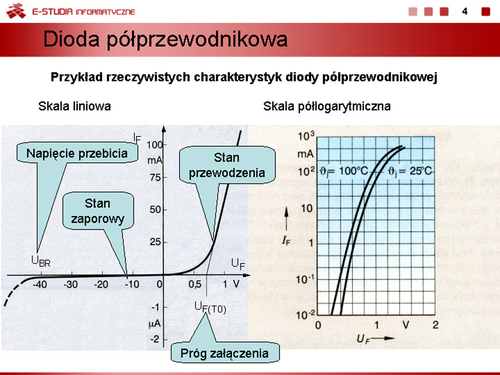
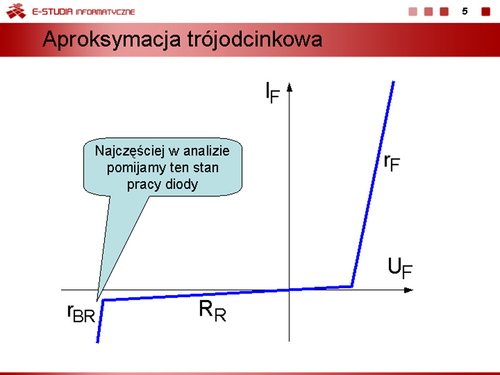
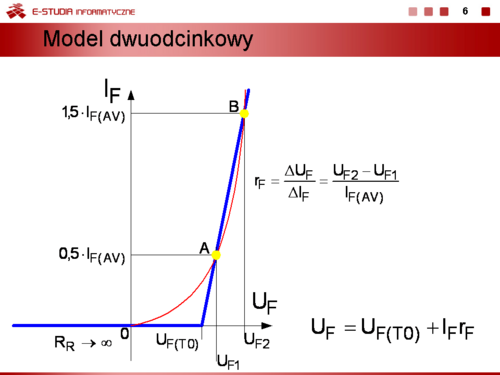
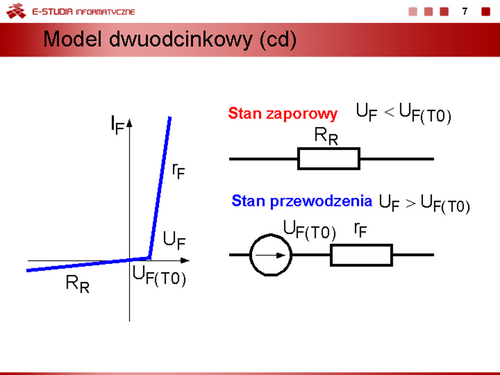
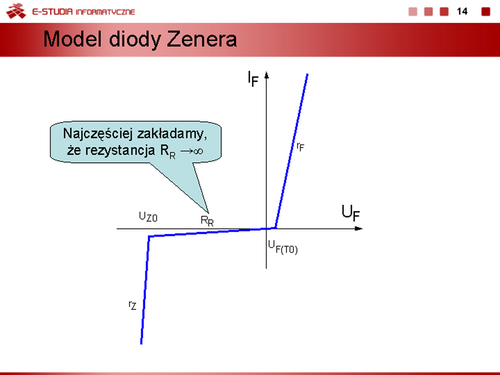
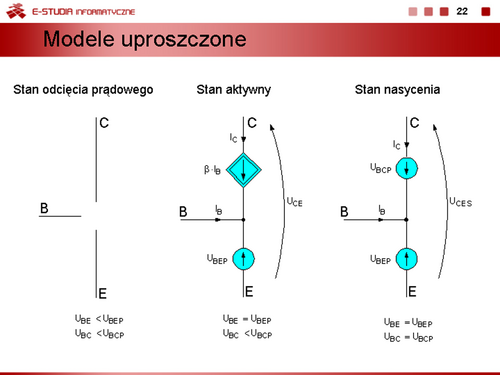
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . |
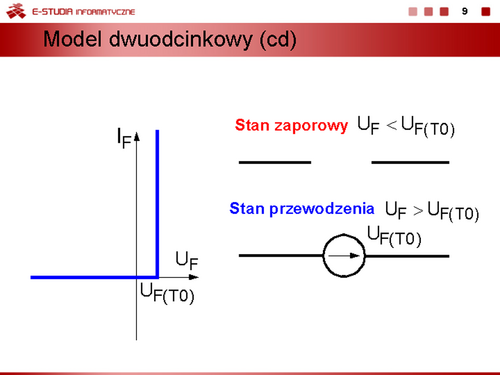 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
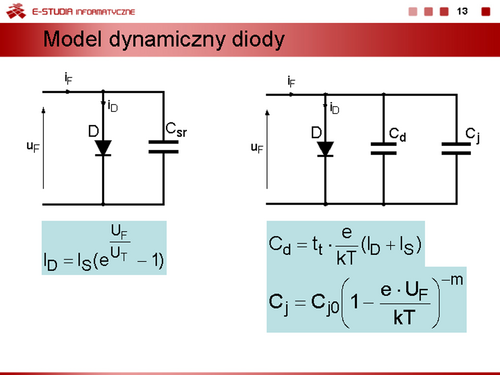
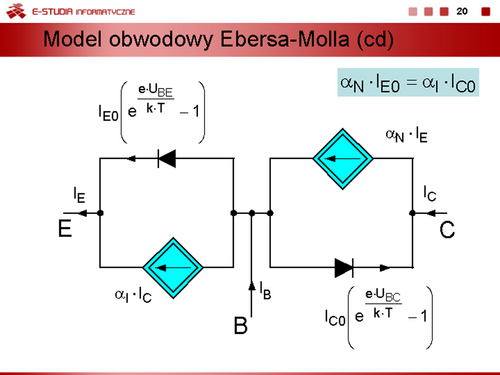
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
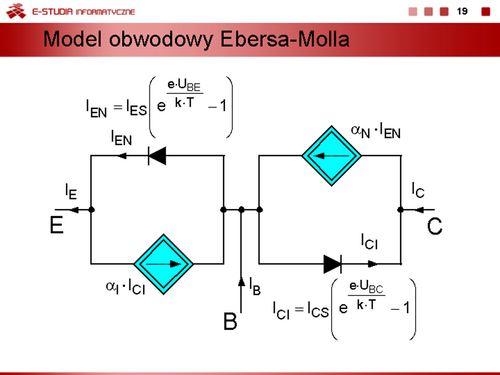 |
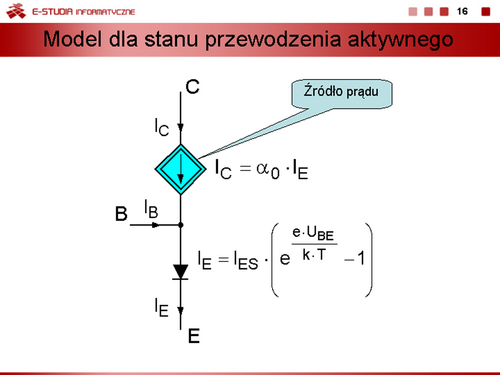
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
 |
 |
 |