PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 256: | Linia 256: | ||
:<math>\displaystyle I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | :<math>\displaystyle I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | ||
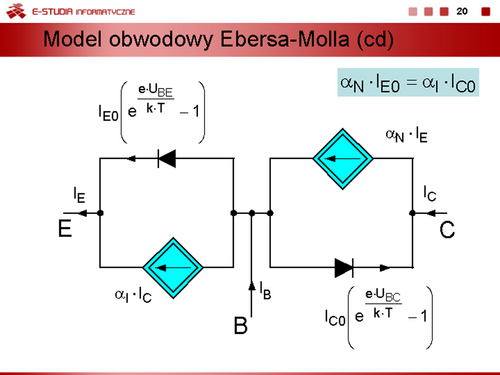
Prądy zerowe tranzystora | Prądy zerowe tranzystora <math>I_{C0} = I_{CB0},\, IE0 = I_{CE0}</math> nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że | ||
<math>\displaystyle \alpha_N\cdot I_{E0}=\alpha_I\cdot I_{C0}</math> | |||
|} | |} | ||
| Linia 264: | Linia 266: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd21.png|thumb|500px]] | ||
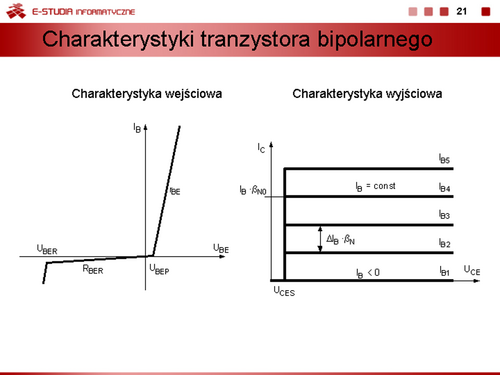
|valign="top"| | |valign="top"|W wypadku prostych obliczeń wystarczająco dobre jest zastąpienie charakterystyk wejściowej i wyjściowej tranzystora odcinkami prostych podobnie jak to ma miejsce przy modelowaniu diod. | ||
Charakterystyka wejściowa jest aproksymowana trzema odcinkami odpowiednio dla stanu przebicia, zaporowego i przewodzenia. Stan przebicia złącza baza-emiter charakteryzuje napięcie przebicia <math>U_{BER}\,</math>. Praktycznie zawsze pomijane. Napięcie progowe, przy którym złącze zaczyna przewodzić jest równe <math>U_{BEP}\,</math>, rezystancja odpowiadająca odcinkowi charakterystyki pomiędzy napięciami <math>U_{BER}\,</math> i <math>U_{BEP}\,</math> ma wartość <math>R_{BE}\,</math>. Często pomija się ją zakładając, że <math>R_{BE} \to \infty\,</math>. Stan przewodzenia charakteryzuje dynamiczna rezystancja wejściowa tranzystora <math>r_{BE}\,</math>. | |||
Charakterystyki wyjściowe to zbiór prostych równoległych, dla których parametrem jest prąd bazy <math>I_B\,</math>. Napięcie <math>U_{CES}\,</math> jest szczątkowym napięciem kolektor-emiter na granicy obszaru aktywnego i obszaru nasycenia. W przybliżeniu jest ono równe różnicy napięć na przewodzących złączach emiterowym i kolektorowym. | |||
<math>U_{CES}=U_{BEP}-U_{BCP}</math> | |||
Ponieważ napięcie <math>U_{BEP}\,</math> jest większe od napięcia <math>U_{BCP}\,</math> to napięcie <math>U_{CES}\,</math> jest dodatnie. Zwykle przyjmuje się, że ma ono wartość około <math>0,2\, V\,</math>. | |||
|} | |} | ||
| Linia 271: | Linia 281: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd22.png|thumb|500px]] | ||
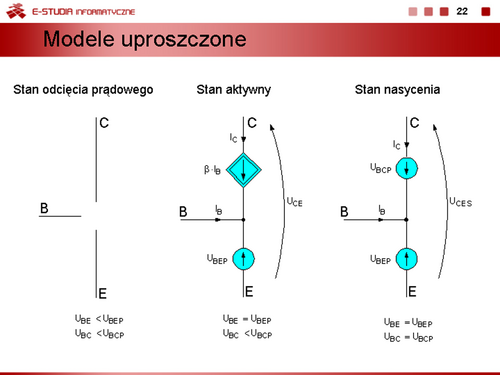
|valign="top"| | |valign="top"|Dla poszczególnych odcinków charakterystyk odpowiadających stanom nasycenia, aktywnemu i odcięcia prądowego można narysować obwodowe, linearyzowane schematy zastępcze tranzystora bipolarnego przedstawione na slajdzie 22. | ||
|} | |} | ||
| Linia 278: | Linia 288: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd23.png|thumb|500px]] | ||
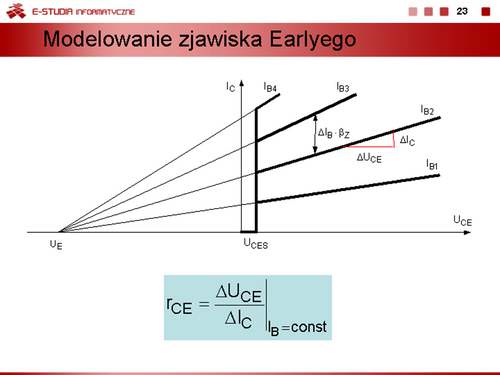
|valign="top"| | |valign="top"|Jeżeli w konkretnym zastosowaniu tranzystora wymagane jest zamodelowanie charakterystyk wyjściowych z uwzględnieniem ich nachylenia, które charakteryzuje dynamiczna rezystancja wyjściowa tranzystora <math>r_{CE}\,</math> lub jej odwrotność dynamiczna (przyrostowa) konduktancja <math>g_{CE}\,</math> wykorzystuje się model uwzględniający zjawisko Earlyego. Polega ono na zmianie długości bazy w warstwach zaporowych złączy wnikających w głąb bazy pod wpływem przyłożonego napięcia. W wyniku skracania się bazy przy dużych napięciach kolektor-emiter wzmocnienie prądowe tranzystora zwiększa się, a to objawia się zwiększaniem nachylenia charakterystyk wyjściowych proporcjonalnie do natężenia prądu bazy. Najprościej zjawisko Earlyego uwzględnia się dobierając eksperymentalnie tzw. potencjał Earlyego <math>U_E\,</math>. | ||
Uwzględniając potencjał <math>U_E\,</math> prąd kolektora można opisać zależnością: | |||
<math>\displaystyle I_C=\beta_{N0}\bigg(1+\frac{U_{CE}}{U_E}\bigg)\cdot I_B=\beta_Z\cdot I_B</math> | |||
przy czym <math>\displaystyle \beta_Z=\beta_{N0}\bigg(1+\frac{U_{CE}}{U_E}\bigg)</math> | |||
<math>\beta_{N0}\,</math> – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy <math>U_{CE} = 0\, V\,</math>. | |||
Z zależności tej można wyznaczyć dynamiczną rezystancję wyjściową tranzystora | |||
<math>\displaystyle r_{CE}=\frac{dU_{CE}}{dI_C}\bigg|_{I_B=const}\approx \frac{U_E}{I_C}</math> | |||
|} | |} | ||
Wersja z 02:46, 13 wrz 2006
 |
Wykład 13. Modele elementów półprzewodnikowych |
 |
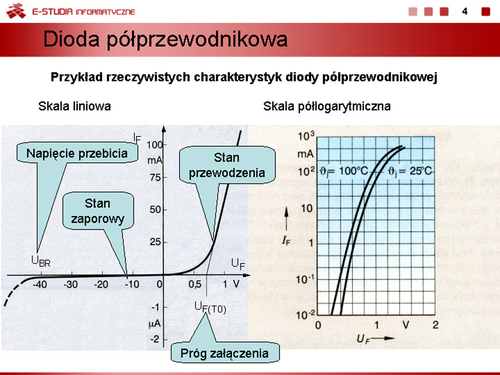
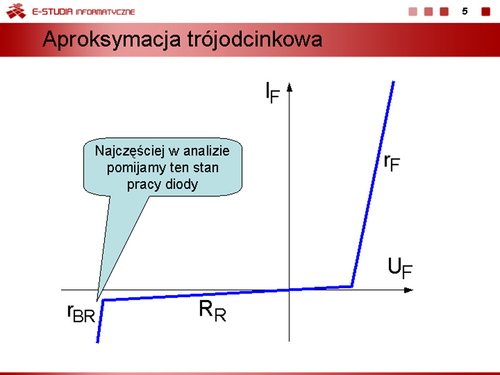
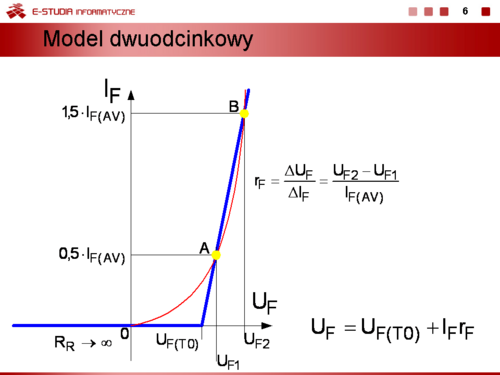
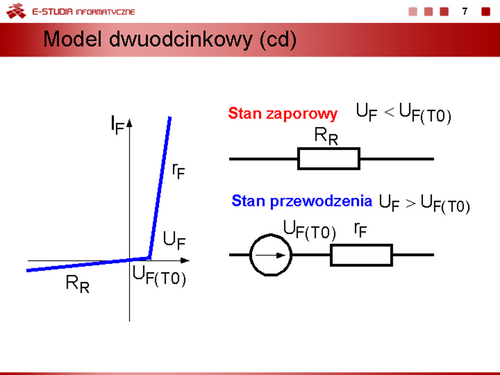
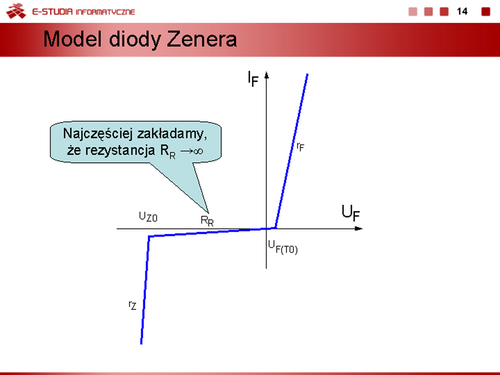
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . |
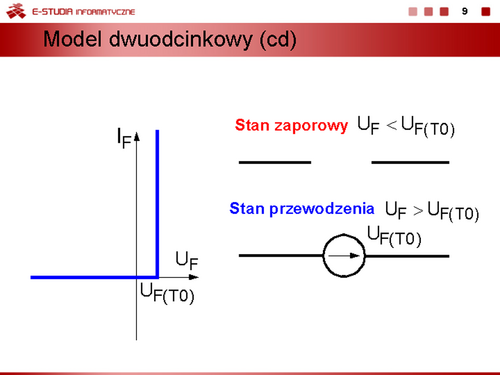 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
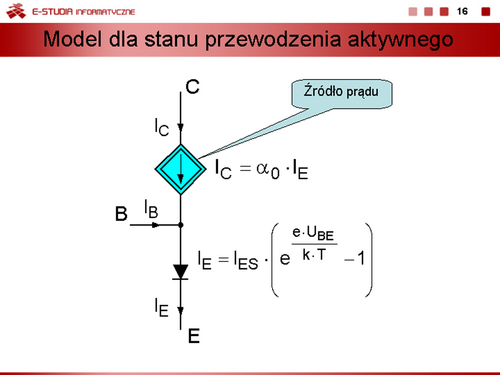
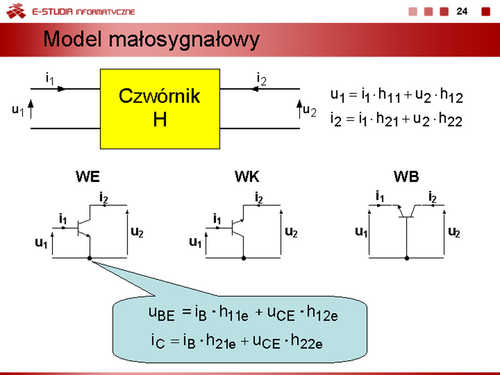
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
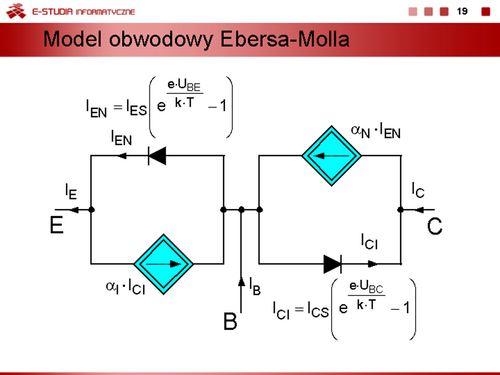 |
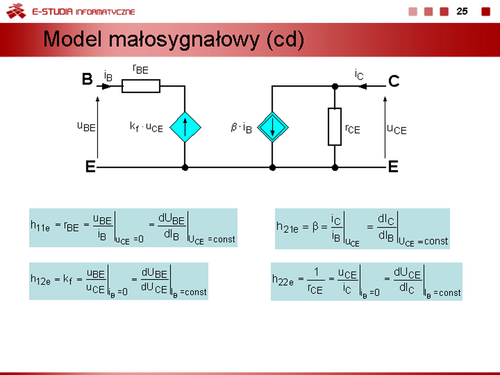
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
 |
 |
 |
 |
 |