PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 218: | Linia 218: | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd17.png|thumb|500px]] | ||
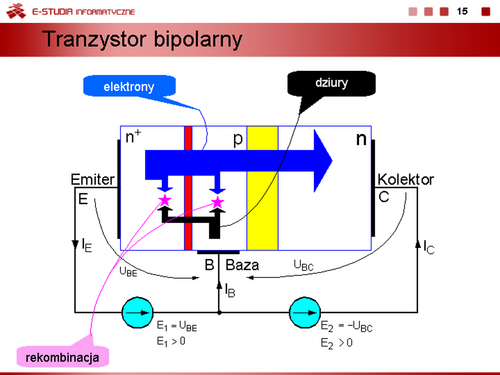
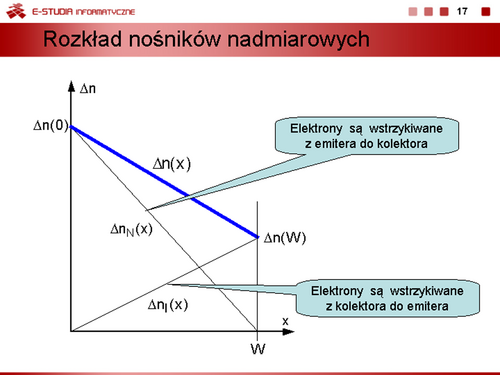
|valign="top"|Jednym z najczęściej stosowanych podstawowych modeli tranzystora bipolarnego | |valign="top"|Jednym z najczęściej stosowanych podstawowych modeli tranzystora bipolarnego | ||
w zakresie dużych sygnałów uwzględniający wszystkie czterech stany pracy tranzystora bipolarnego jest Model Ebersa-Molla opublikowany przez J. J. Ebersa i J. L. Molla w 1954 roku. Aby wyjaśnić ideę tego modelu załóżmy, że dla tranzystora npn pracującego w stanie nasycenia krzywa rozkładu nośników nadmiarowych <math>Delta n(x)\,</math> w bazie ma kształt jak na rysunku przedstawionym na slajdzie 17 i zawiera dwie składowe <math>Delta | w zakresie dużych sygnałów uwzględniający wszystkie czterech stany pracy tranzystora bipolarnego jest Model Ebersa-Molla opublikowany przez J. J. Ebersa i J. L. Molla w 1954 roku. Aby wyjaśnić ideę tego modelu załóżmy, że dla tranzystora npn pracującego w stanie nasycenia krzywa rozkładu nośników nadmiarowych <math>\Delta n(x)\,</math> w bazie ma kształt jak na rysunku przedstawionym na slajdzie 17 i zawiera dwie składowe <math>\Delta n_N(x)\,</math> i <math>\Delta n_I(x)\,</math>. Oznacza to, że przy pracy tranzystora w stanie nasycenia występuje jednocześnie przepływ elektronów do kolektora wstrzykiwanych przez złącze emiterowe (transmisja normalna, indeks <math>N\,</math>), oraz przepływ elektronów do emitera wstrzykiwanych przez złącze kolektorowe (transmisja inwersyjna, indeks <math>I\,</math>). Dla kierunku transmisji normalnej definiuje się współczynniki wzmocnienia prądowego <math>\alpha_N\,</math> (lub <math>\beta_N\,</math>), a dla transmisji inwersyjnej <math>\alpha_I\,</math> (lub <math>\beta_I\,</math>). Wartości odpowiednich współczynników nie są sobie równe, gdyż struktura tranzystora nie jest symetryczna. | ||
|} | |} | ||
| Linia 226: | Linia 226: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd18.png|thumb|500px]] | ||
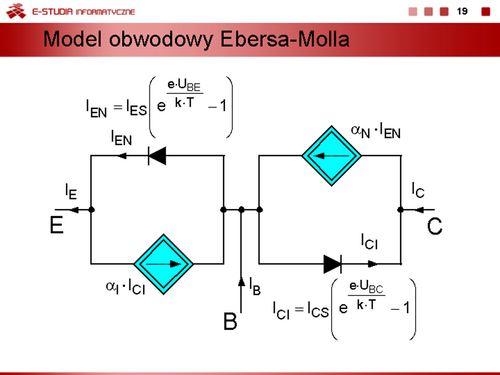
|valign="top"| | |valign="top"|Można zatem zapisać równania, określające związki prądów <math>I_C\,</math>, <math>I_E\,</math> od napięć złączowych <math>U_{BE}\,</math>, <math>U_{BC}\,</math> w postaci | ||
<math>\displaystyle I_E=I_{EN}-\alpha_I \cdot I_{CI}=I_{ES}\bigg(e^{\displaystyle \frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)-\alpha_I\cdot I_{CS}\bigg(e^{\displaystyle \frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | |||
<math>\displaystyle I_C=\alpha_N\cdot I_{EN}-I_{CI}=\alpha_N\cdot I_{ES}\bigg(e^{\displaystyle \frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)- I_{CS}\bigg(e^{\displaystyle \frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | |||
Równania te nazywamy równaniami Ebersa-Molla. | |||
|} | |} | ||
| Linia 233: | Linia 239: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd19.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd19.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. | ||
|} | |} | ||
| Linia 240: | Linia 246: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd20.png|thumb|500px]] | ||
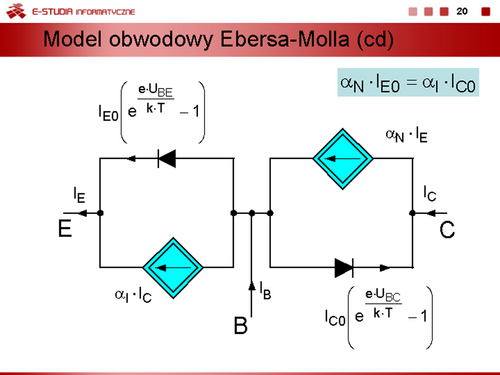
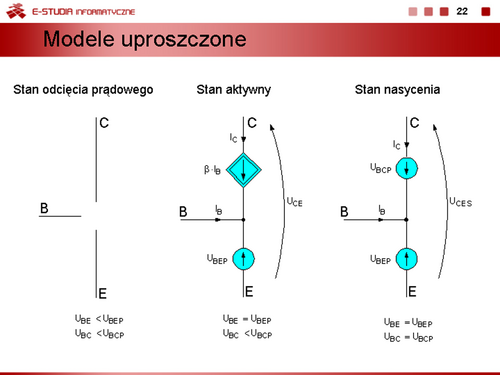
|valign="top"| | |valign="top"|Zwykle wygodniej jest posługiwać się modelem Ebersa-Molla, w którym sterowane źródła prądowe są uzależnione od prądów zewnętrznych tranzystora. | ||
<math>\displaystyle I_E=\alpha_I \cdot I_C+I_{E0}\bigg(e^{\displaystyle \frac{e\cdot U_{BE}}{k\cdot T}}-1 \bigg)</math> | |||
<math>\displaystyle I_C=\alpha_N \cdot I_E-I_{C0}\bigg(e^{\displaystyle \frac{e\cdot U_{BC}}{k\cdot T}}-1 \bigg)</math> | |||
gdzie <math>\displaystyle I_{E0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{ES}</math> | |||
:<math>\displaystyle I_{C0}=(1-\alpha_I\cdot \alpha_N)\cdot I_{CS}</math> | |||
Prądy zerowe tranzystora IC0 = ICB0, IE0 = ICE0 nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, żePrądy zerowe tranzystora IC0 = ICB0, IE0 = ICE0 nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że | |||
|} | |} | ||
Wersja z 02:27, 13 wrz 2006
 |
Wykład 13. Modele elementów półprzewodnikowych |
 |
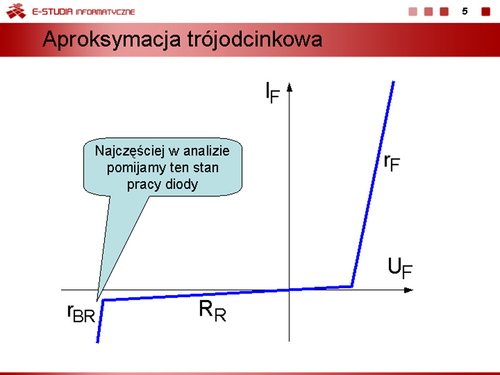
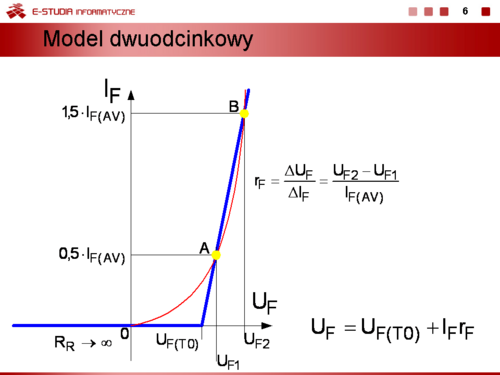
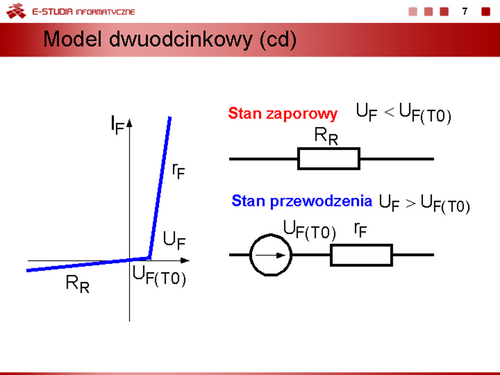
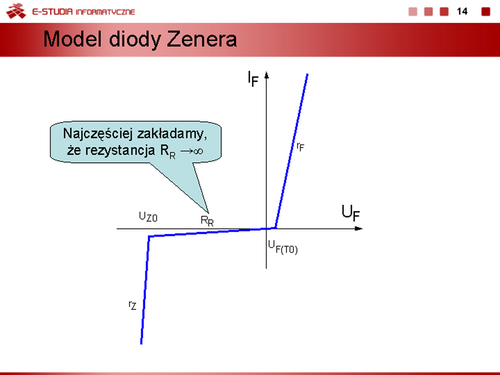
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . |
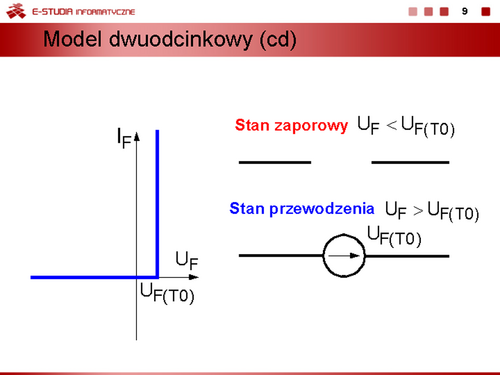 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
 |
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |
 |
 |
 |
 |
 |
 |
 |
 |