PS Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 166: | Linia 166: | ||
|valign="top"| | |valign="top"| | ||
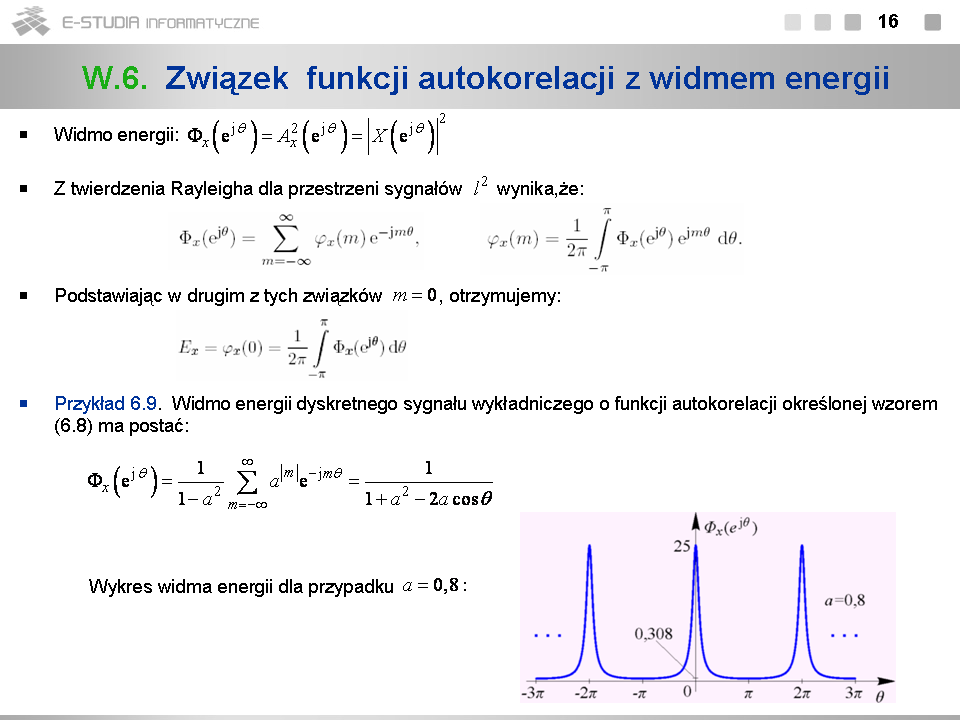
*W przykładzie 6.8 funkcję autokorelacji można wyznaczyć w postaci zamkniętej. W obliczeniach korzystamy ze wzoru na sumę nieskończonego szeregu geometrycznego. | *W przykładzie 6.8 funkcję autokorelacji można wyznaczyć w postaci zamkniętej. W obliczeniach korzystamy ze wzoru na sumę nieskończonego szeregu geometrycznego. | ||
*Im parametr <math>a\,</math> jest mniejszy, tym szybciej zanika korelacja między próbkami sygnału. Jeśli <math>a\to | *Im parametr <math>a\,</math> jest mniejszy, tym szybciej zanika korelacja między próbkami sygnału. Jeśli <math>a\to 1\,</math> , sygnał dąży do dyskretnego skoku jednostkowego <math>1[n]\,</math> , a funkcja autokorelacji dąży do funkcji stałej równej <math>1/2\,</math> dla każdego <math>m\,</math>. Aby to pokazać, trzeba jednak dokonać odpowiedniego przejścia granicznego. | ||
| Linia 184: | Linia 184: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd17.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd17.png]] | ||
|valign="top"| | |||
*W przypadku dwóch różnych sygnałów dyskretnych ich właściwości korelacyjne charakteryzują funkcje korelacji wzajemnej. Definicje i właściwości tych funkcji są analogiczne jak w przypadku sygnałów analogowych. | *W przypadku dwóch różnych sygnałów dyskretnych ich właściwości korelacyjne charakteryzują funkcje korelacji wzajemnej. Definicje i właściwości tych funkcji są analogiczne jak w przypadku sygnałów analogowych. | ||
*Analogicznie do przypadku sygnałów analogowych definiuje się również widma energii wzajemnej sygnałów dyskretnych. | *Analogicznie do przypadku sygnałów analogowych definiuje się również widma energii wzajemnej sygnałów dyskretnych. | ||
| Linia 193: | Linia 194: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd18.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd18.png]] | ||
|valign="top"| | |valign="top"| | ||
*Funkcja autokorelacji sygnału dyskretnego o ograniczonej mocy jest definiowana w sensie granicznym. Funkcję tę oznaczamy taką samą literą | *Funkcja autokorelacji sygnału dyskretnego o ograniczonej mocy jest definiowana w sensie granicznym. Funkcję tę oznaczamy taką samą literą <math>\psi\,</math> jak w przypadku sygnałów analogowych o ograniczonej mocy. | ||
*Właściwości funkcji autokorelacji sygnałów dyskretnych o ograniczonej mocy są analogiczne jak w przypadku sygnałów analogowych. W szczególności wartość funkcji autokorelacji w zerze jest równa mocy sygnału. | |||
*Funkcja autokorelacji dyskretnego sygnału harmonicznego jest dyskretną kosinusoidą i nie zależy od fazy początkowej sygnału. Jej wartość w punkcie <math>m=0</math> jest równa mocy sygnału <math>X_0^2/2\,</math>. | |||
|} | |} | ||
| Linia 206: | Linia 204: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd19.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd19.png]] | ||
|valign="top"| | |valign="top"| | ||
*Podobnie jak w przypadku sygnałów analogowych, widmo mocy sygnału dyskretnego <math>\Phi_N(e^{j\theta})\,</math> o ograniczonej mocy jest zdefiniowane jako granica ciągu widm energii <math>x[n]\,</math> środkowych segmentów tego sygnału o czasie trwania <math>[-N, N]\,</math> odniesionych do szerokości <math>2N+1\,</math> tych segmentów przy <math>N\to \infty\,</math> . | |||
*W przypadku sygnałów <math>N\,</math> -okresowych ich funkcje autokorelacji są również <math>N\,</math> -okresowe. Współczynnikami <math>\Psi(k)\,</math> rozwinięcia funkcji autokorelacji <math>\overline{\psi}_x [m]\,</math> sygnału <math>N\,</math> -okresowego <math>\overline{x}[n]\,</math> w dyskretny szereg Fouriera są kwadraty <math>|X(k)|^2\,</math> modułów współczynników <math>X(k)\,</math> rozwinięcia w dyskretny szereg Fouriera sygnału <math>\overline{x}[n]\,</math>. | |||
*Moc sygnału <math>N\,</math> -okresowego jest sumą za okres <math>N\,</math> wartości <math>\Psi(k)\,</math> jego widma mocy. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||