PS Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 28: | Linia 28: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd3.png]] | ||
|valign="top"| | |valign="top"| | ||
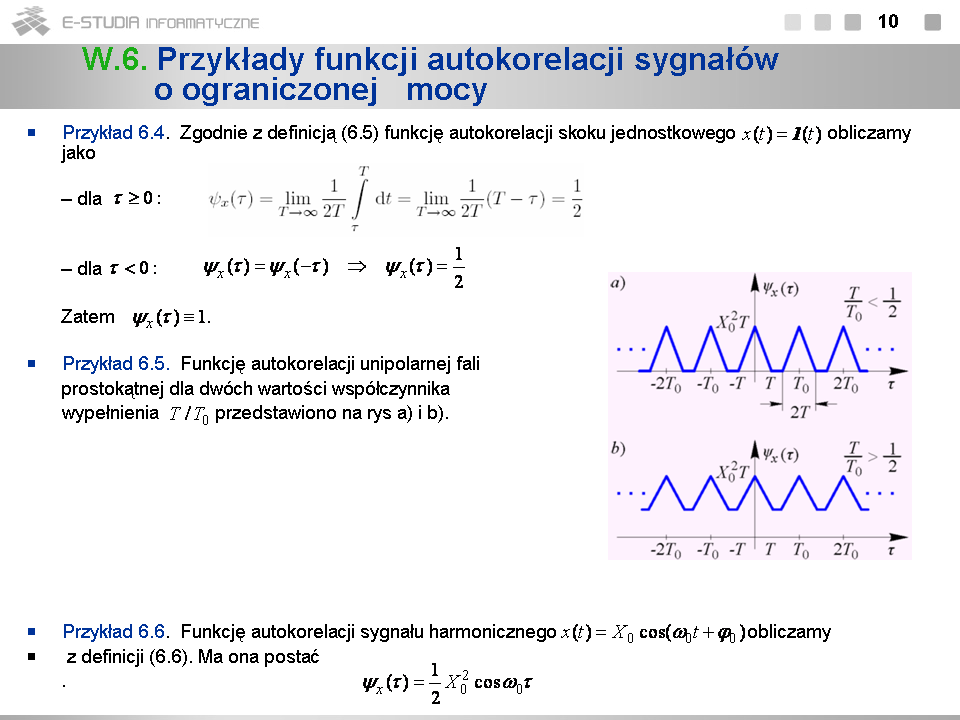
*Przedstawione na rysunku funkcje autokorelacji można wyznaczyć wprost z definicji. Wszystkie funkcje mają jedyne maksimum w punkcie <math>\tau=0</math>. | |||
*Funkcja autokorelacji impulsu prostokątnego jest trójkątna. Sposób jej konstrukcji jest pokazany na rys. e. | |||
*Trójkątny kształt funkcji autokorelacji występuje również w przypadku ciągu impulsów prostokątnych i prostokątnego impulsu radiowego. | |||
|} | |} | ||
| Linia 35: | Linia 39: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
*Słuszność pary transformat (6.3) można wykazać na podstawie twierdzenia Rayleigha dla klasy sygnałów <math>L^2\,</math> i twierdzenia o przesunięciu. Ponieważ <math>F\, [x(t-\tau)]=X(\omega)e^{-j\omega \tau}</math> , zatem: | |||
<math>\int_{-\infty}^{\infty} x(t)x^{*}(t-\tau)\, d\tau=\frac{1}{2\pi}\int_{-\infty}^{\infty} X(\omega)X^{*}(\omega)e^{j\omega \tau}\, d\omega=\frac{1}{2\pi}\int_{-\infty}^{\infty} |X(\omega)|^2e^{j\omega \tau}\, d\omega</math> | |||
*Energię sygnału można obliczyć: | |||
**w dziedzinie czasu, jako całkę z kwadratu modułu sygnału, | |||
**w dziedzinie korelacyjnej, jako <math>\varphi_x(0)</math>, | |||
**w dziedzinie częstotliwości, jako całkę z widma energii podzieloną przez <math>2\pi\,</math>. | |||
|} | |} | ||
| Linia 42: | Linia 56: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd5.png]] | ||
|valign="top"| | |valign="top"| | ||
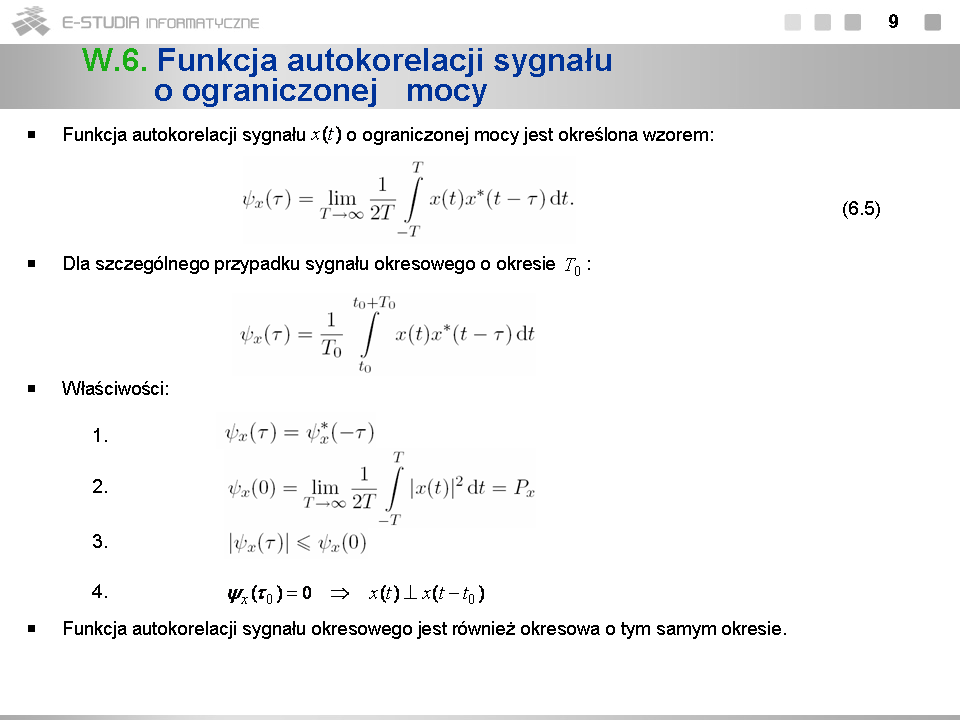
*Widmo energii jest zawsze funkcją rzeczywistą parzystą i opisuje rozkład energii wzdłuż osi częstotliwości. Energię sygnału zawartą w przedziale pulsacji <math>[\omega_1, omega_2]\,</math> można wyznaczyć, obliczając całkę | |||
<math>E_x(\omega_1, \omega_2)=\frac{1}{\pi}\int_{\omega_1}^{\omega_2} \Phi_x(\omega)\, d\omega</math> (por. rys. a). | |||
*Funkcja autokorelacji idealnego sygnału dolnopasmowego <math>x(t)=X_0 Sa\omega_0 t</math> ma również kształt funkcji <math>Sa\,</math>. Wynika to z faktu, że zarówno widmo amplitudowe tego sygnału, jak i jego widmo energii są prostokątne. | |||
|} | |} | ||
| Linia 49: | Linia 69: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
*Związki między sygnałem i jego charakterystykami w dziedzinie częstotliwości i dziedzinie korelacyjnej ilustruje prosty diagram. Strzałki podwójne oznaczają na nim związki wzajemnie jednoznaczne, tj. jednoznaczne przejścia od jednej do drugiej wielkości , natomiast strzałki pojedyncze oznaczają przejście tylko w jedną stronę. | |||
*Funkcja autokorelacji sygnału stanowi jedynie częściowy opis sygnału. Znając te funkcję możemy odtworzyć widmo amplitudowe sygnału, tracimy jednak informację o widmie fazowym. | |||
*Podana definicja ''efektywnego czasu korelacji'' ma sens dla przypadku sygnałów, których funkcja autokorelacji maleje monotonicznie. Dla sygnałów o funkcji autokorelacji dążącej do zera oscylacyjnie można wprowadzić inne miary czasu korelacji. | |||
*Zasada nieoznaczoności pozostaje w mocy bez względu na sposób definiowania efektywnego czasu korelacji i efektywnej szerokości widma. | |||
|} | |} | ||
Wersja z 14:43, 5 wrz 2006

|

|
|
|

|

|

|

|
|
|

|

|

|