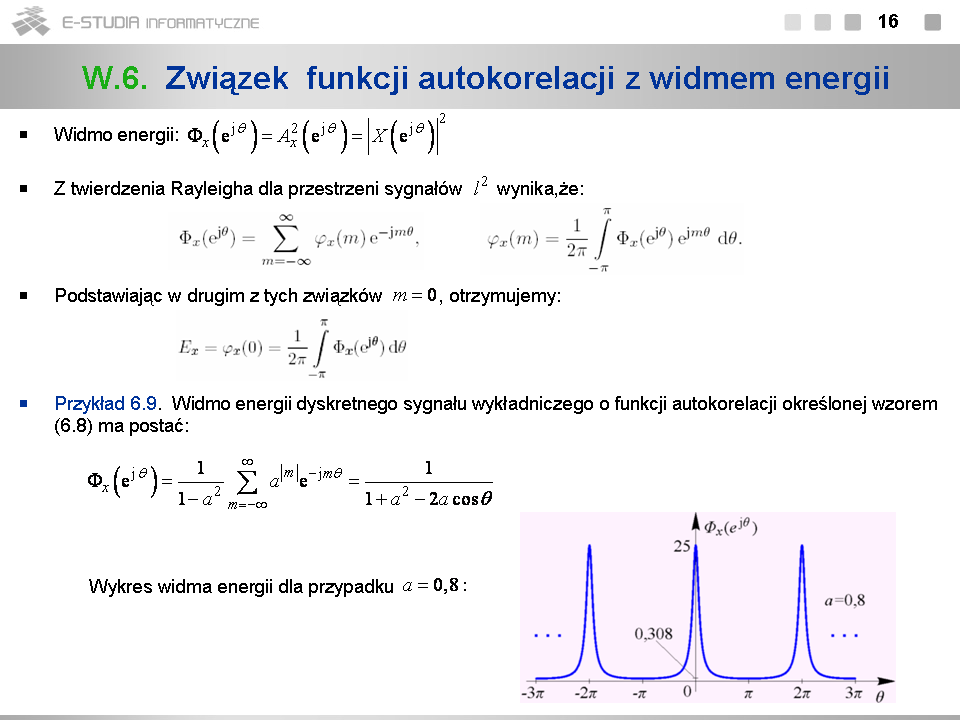
|
|
| Linia 2: |
Linia 2: |
| |width="500px" valign="top"|[[Grafika:PS_M6_Slajd1.png]] | | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd1.png]] |
| |valign="top"| | | |valign="top"| |
| | *W zastosowaniach teorii sygnałów często porównujemy analizowanego sygnału z innym sygnałem, w szczególności ¬z swoją własną przesuniętą w czasie kopią. Podobieństwo sygnałów można charakteryzować za pomocą funkcji korelacyjnych. |
| | *Przypomnijmy, że na podstawie iloczynu skalarnego możemy wyznaczyć zarówno odległość dwóch sygnałów, jak i kąt między nimi w danej przestrzeni Hilberta. |
| | *Jeśli <math>x(t)\in L^2\,</math> , to także <math>x_{\tau}(t)\in L^2</math>. |
| | *Dla różnych wartości przesunięcia <math>\tau\,</math> całka definicyjna (6.1) przybiera różne wartości. W ten sposób otrzymujemy zależność funkcyjną od zmiennej <math>\tau\,</math> . Dla ustalonego <math>\tau\,</math> wartość funkcji autokorelacji jest polem pod wykresem iloczynu sygnału nieprzesuniętego i przesuniętego. |
| | *Definicja (6.1) została podana od razu dla sygnałów zespolonych. Przedrostek „auto” oznacza, że funkcja korelacyjna (6.1) opisuje korelację czasową między danym sygnałem a wersją przesuniętą tego samego sygnału. Podkreślamy to dodając do symbolu <math>"\varphi"\,</math> funkcji autokorelacji indeks sygnału <math>"x"\,</math>. |
|
| |
|
| |} | | |} |