Układy elektroniczne i technika pomiarowa/Moduł 7: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 225: | Linia 225: | ||
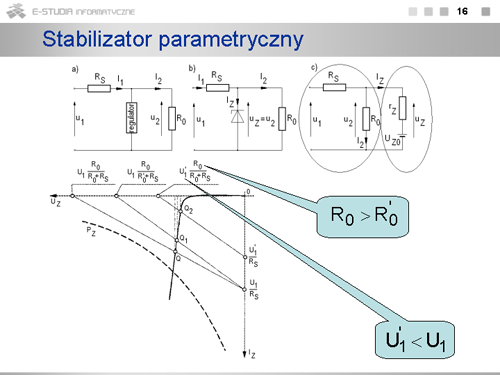
Zasadę działania układu ilustruje rysunek. Napięcie wyjściowe stabilizatora jest równe napięciu na diodzie Zenera, dlatego badanie wpływu napięcia wejściowego i rezystancji obciążenia na wartość napięcia <math>U_2\,</math> polega na analizie położenia punktu pracy na charakterystyce diody. Dwa skrajne położenia odpowiadają stanom, kiedy dioda praktycznie nie przewodzi <math>I_2\approx 0\, A</math> , <math>U_2\approx U_{Z0}</math> oraz kiedy przewodzi prąd o wartości dopuszczalnej <math>I_Z = I_{ZMAX}</math> , gdzie <math>I_{ZMAX} = P_Z/U_{Z0}</math>. Jeżeli na charakterystyce diody narysuje się tzw. prostą obciążenia (charakterystyka prądowo – napięciowa pozostałej, liniowej części obwodu stabilizatora) to punkt przecięcia tej prostej z nieliniową charakterystyką diody Zenera wyznacza punkt pracy diody Zenera i jednocześnie punkt pracy obwodu do niej dołączonego. Zmieniając odpowiednio parametry diody Zenera (napięcie przebicia <math>U_{Z0}\,</math> , rezystancja dynamiczna <math>r_Z\,</math>) i rezystancje obwodu <math>(R_S, R_0)\,</math> można dokładnie prześledzić ruchy punktu pracy po charakterystyce diody i charakterystykach elementów z jakich jest zbudowany stabilizator. | Zasadę działania układu ilustruje rysunek. Napięcie wyjściowe stabilizatora jest równe napięciu na diodzie Zenera, dlatego badanie wpływu napięcia wejściowego i rezystancji obciążenia na wartość napięcia <math>U_2\,</math> polega na analizie położenia punktu pracy na charakterystyce diody. Dwa skrajne położenia odpowiadają stanom, kiedy dioda praktycznie nie przewodzi <math>I_2\approx 0\, A</math> , <math>U_2\approx U_{Z0}</math> oraz kiedy przewodzi prąd o wartości dopuszczalnej <math>I_Z = I_{ZMAX}</math> , gdzie <math>I_{ZMAX} = P_Z/U_{Z0}</math>. Jeżeli na charakterystyce diody narysuje się tzw. prostą obciążenia (charakterystyka prądowo – napięciowa pozostałej, liniowej części obwodu stabilizatora) to punkt przecięcia tej prostej z nieliniową charakterystyką diody Zenera wyznacza punkt pracy diody Zenera i jednocześnie punkt pracy obwodu do niej dołączonego. Zmieniając odpowiednio parametry diody Zenera (napięcie przebicia <math>U_{Z0}\,</math> , rezystancja dynamiczna <math>r_Z\,</math>) i rezystancje obwodu <math>(R_S, R_0)\,</math> można dokładnie prześledzić ruchy punktu pracy po charakterystyce diody i charakterystykach elementów z jakich jest zbudowany stabilizator. | ||
Przyjmując dwuodcinkową aproksymację charakterystyki diody Zenera oraz, że punkt pracy diody leży na odcinku umożliwiającym stabilizację napięcia można napisać: | |||
:<math>U_2=U_Z=U_{Z0}+I_Z\cdot r_Z</math> | |||
<math>U_1=(I_Z+I_2)\cdot R_S +U_2=\left(\frac{U_2-U_{Z0}}{r_Z}+\frac{U_2}{U_0}\right)\cdot R_S+U_{Z0}+I_Z\cdot r_Z</math> | |||
Po przekształceniu uzyskuje się: | |||
<math>U_2=\frac{r_Z}{R_S+r_Z}U_1-\frac{R_S \cdot r_Z}{R_S+r_Z}I_2+\frac{R_S}{R_S+r_Z}U_{Z0}</math> | |||
Wyznaczając odpowiednie pochodne cząstkowe można obliczyć poszczególne współczynniki stabilizacji: | |||
<math>\begin{matrix} G_U=\frac{r_Z}{R_S+r_Z} & r_{WY}=\frac{R_S\cdot r_Z}{R_S+r_Z} & \gamma_T=\frac{R_S}{R_S+r_Z}\cdot \frac{dU_{Z0}}{dT} \end{matrix}</math> | |||
Decydujący wpływ na jakość stabilizacji mają: wartości rezystancji dynamicznej <math>r_Z\,</math> | |||
i współczynnik temperaturowy <math>dU_{Z0}/dT</math> stabilistora. | |||
|} | |} | ||
Wersja z 12:05, 4 wrz 2006
wersja beta
UKŁADY ELEKTRONICZNE I TECHNIKA POMIAROWA
Moduł 7 - Układy zasilające

|
Wykład 7. Układy zasilające. |

|
Klasyczny układ zasilacza składa się z czterech podstawowych elementów: transformatora sieciowego, prostownika, filtru i jeżeli to jest potrzebne ze stabilizatora napięcia lub rzadziej prądu. |

|
Prostowniki sieciowe sterowane buduje się zastępując diody prostownicze w układach niesterowanych, tyrystorami. |
|
opis |

|
opis |
|
opis |

|
opis |
|
|
opis |

|
opis |
</math>