MN04LAB: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
= | <!-- | ||
Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php | |||
--> | |||
=Ćwiczenia: rozwiązywanie układów równań liniowych= | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Mnożyć przez odwrotność to nie zawsze to samo...</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
W Octave układ równań <math>\displaystyle Ax=b</math> rozwiązujemy korzystając z "operatora | W Octave układ równań <math>\displaystyle Ax=b</math> rozwiązujemy korzystając z "operatora | ||
rozwiązywania równania" | rozwiązywania równania" | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
x | x = A \ b; | ||
</pre></div> | </pre></div> | ||
| Linia 18: | Linia 22: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
x | x = inv(A)*b; | ||
</pre></div> | </pre></div> | ||
| Linia 35: | Linia 39: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
N | N = 400; A = rand(N,N);x = rand(N,1); b = A*x; | ||
tic; X | tic; X = A \ b; tX = toc; | ||
tic; Y | tic; Y = inv(A)*b; tY = toc; | ||
[norm(X-x)/norm(x), norm(Y-x)/norm(x); tX, tY] | [norm(X-x)/norm(x), norm(Y-x)/norm(x); tX, tY] | ||
</pre></div> | </pre></div> | ||
| Linia 43: | Linia 47: | ||
<div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | <div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | ||
ans | ans = | ||
1.9861e-13 2.8687e-13 | 1.9861e-13 2.8687e-13 | ||
2.3644e-01 4.0609e-01 | 2.3644e-01 4.0609e-01 | ||
| Linia 50: | Linia 54: | ||
Wyszło (z grubsza) dwa razy szybciej i dwa razy dokładniej. | Wyszło (z grubsza) dwa razy szybciej i dwa razy dokładniej. | ||
</div></div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Wybór elementu głównego jest naprawdę ważny!</span> | |||
<div class="exercise"> | |||
Rozwiąż prosty układ równań | |||
<center><math>\displaystyle \aligned 10^{-18} x_1 + x_2 &= 1,\\ | |||
x_1 + 2x_2 &= 4, | |||
\endaligned</math></center> | |||
czterema sposobami: | |||
* na kartce papieru (dokładnie!) | |||
* w komputerze, w arytmetyce podwójnej precyzji, korzystając z rozkładu LU <strong>bez wyboru elementu głównego</strong> | |||
* jak poprzednio, ale <strong>z wyborem elementu głównego w kolumnie</strong> | |||
* w LAPACKu lub Octave. | |||
Porównaj uzyskane rozwiązania i wyciągnij wnioski. | |||
</div></div> | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
Rozwiązanie uzyskane bez wyboru elementu głównego jest bardzo mało precyzyjne <math>\displaystyle x_1</math> jest obarczone bardzo duzym błędem! Prosta analiza poazuje, że winę za to ponosi bardzo wielki współczynnik w macierzy <math>\displaystyle L</math>. Tak nie jest, gdy stosujemy wybór elementu: elementy <math>\displaystyle L</math> są zawsze mniejsze od 1. Dlatego inne rozwiązania numeryczne dają w przypadku naszej macierzy wynik, będący bardzo dobrym przybliżeniem wyniku dokładnego. ''A propos:'' Octave korzysta z <code>DGESV</code> LAPACKa, a <code>DGESV</code> korzysta z wyboru w kolumnie... | |||
</div></div></div> | </div></div></div> | ||
| Linia 65: | Linia 92: | ||
Przetestuj tę funkcję na kilku macierzach i porównaj czas jego działania z czasem | Przetestuj tę funkcję na kilku macierzach i porównaj czas jego działania z czasem | ||
wykonania operacji <code>x | wykonania operacji <code>x = A\b</code>. | ||
Spróbuj zastosować swój algorytm do kilku specjalnych macierzy: | Spróbuj zastosować swój algorytm do kilku specjalnych macierzy: | ||
| Linia 78: | Linia 105: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
function [L,U] | function [L,U] = lufa(A) | ||
# Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | # Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | ||
# czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | # czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | ||
N | N = size(A,1); | ||
for k | for k=1:N-1 | ||
if (A(k,k) | if (A(k,k) == 0.0) | ||
return; | return; | ||
end | end | ||
for i | for i=k+1:N #wyznaczenie <math>\displaystyle k</math>-tej kolumny <math>\displaystyle L</math> | ||
A(i,k) | A(i,k) = A(i,k)/A(k,k); | ||
end | end | ||
for j | for j=k+1:N #modyfikacja podmacierzy <math>\displaystyle A_{22} = A_{22} - l_{21}u_{12}^T</math> | ||
for i | for i=k+1:N | ||
A(i,j) - | A(i,j) -= A(i,k)*A(k,j); | ||
end | end | ||
end | end | ||
end | end | ||
L | L = tril(A,-1) + eye(N); | ||
U | U = triu(A); | ||
end | end | ||
</pre></div> | </pre></div> | ||
| Linia 108: | Linia 135: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
function [L,U] | function [L,U] = lufb(A) | ||
# Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | # Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | ||
# czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | # czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | ||
N | N = size(A,1); | ||
for k | for k=1:N-1 | ||
if (A(k,k) | if (A(k,k) == 0.0) | ||
return; | return; | ||
end | end | ||
#wyznaczenie <math>\displaystyle k</math>-tej kolumny <math>\displaystyle L</math> | #wyznaczenie <math>\displaystyle k</math>-tej kolumny <math>\displaystyle L</math> | ||
A(k+1:N,k) | A(k+1:N,k) = A(k+1:N,k)/A(k,k); | ||
#modyfikacja podmacierzy <math>\displaystyle A_{22} = A_{22} - l_{21}u_{12}^T</math> | #modyfikacja podmacierzy <math>\displaystyle A_{22} = A_{22} - l_{21}u_{12}^T</math> | ||
A(k+1:N,k+1:N) - | A(k+1:N,k+1:N) -= A(k+1:N,k)*A(k,k+1:N); | ||
end | end | ||
L | L = tril(A,-1) + eye(N); | ||
U | U = triu(A); | ||
end | end | ||
</pre></div> | </pre></div> | ||
| Linia 129: | Linia 156: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
[Kod testujący lufa(0 i lufb()] | [Kod testujący lufa(0 i lufb()] | ||
N | N = 100; | ||
A | A = rand(N) + 1000*eye(N); | ||
format short e; | format short e; | ||
t | t = ta = tb = Inf; | ||
K | K = 5; | ||
for i | for i = 0:K | ||
tic; [L, U] | tic; [L, U] = lu(A); t = min(t,toc); | ||
tic; [La, Ua] | tic; [La, Ua] = lufa(A); ta = min(ta,toc); | ||
tic; [Lb, Ub] | tic; [Lb, Ub] = lufb(A); tb = min(tb,toc); | ||
end | end | ||
| Linia 153: | Linia 180: | ||
{| border=1 | {| border=1 | ||
|+ <span style="font-variant:small-caps"> | |+ <span style="font-variant:small-caps"> </span> | ||
|- | |- | ||
| Implementacja || lu (oryginalne) || lufa || lufb | | Implementacja || lu (oryginalne) || lufa || lufb | ||
| Linia 182: | Linia 209: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
function x | function x = sol(L,U,b) | ||
x | x = U \ ( L \ b); | ||
end | end | ||
</pre></div> | </pre></div> | ||
| Linia 195: | Linia 222: | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Czy Twoje programy działają <strong>naprawdę</strong> szybko?</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
Zrób zadanie poprzednie w C i | Zrób zadanie poprzednie programując, niczym Zosia-Samosia, wszystko od początku do końca w czystym C. Porównaj czasy działania Twojego programu i programu wywołującego po prostu procedurę biblioteczną LAPACKa | ||
<code>DGESV</code>, najlepiej wspartą dobrze podrasowanymi BLASami. | <code>DGESV</code>, najlepiej wspartą dobrze podrasowanymi BLASami. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | |||
<div style="font-size:smaller; background-color:#efe"> To zadanie to wyzwanie! </div> | |||
</div></div> | |||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
No tak, namawiamy Cię do zmierzenia się z LAPACKiem i ATLASem.... | |||
Prościutki program --- po prostu tłumaczącu algorytm z wykładu bezpośrednio | |||
na C --- u nas spisał | |||
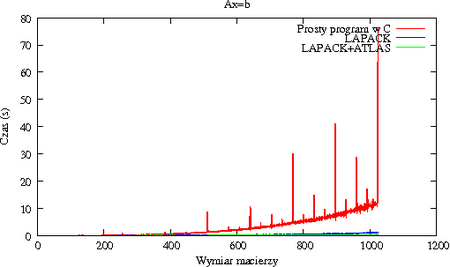
się, dla macierzy wymiaru <math>\displaystyle N=1\ldots 1024</math>, następująco: | |||
[[Image:MNdegsvtiming.png|thumb|450px|center|Prosty solver w C kontra LAPACK i LAPACK z ATLASem. | |||
Zwróć uwagę na piki zwykłego kodu dla <math>\displaystyle N</math> będących potęgami dwójki]] | |||
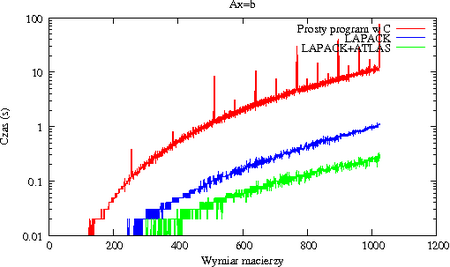
[[Image:MNdegsvtiminglogscale.png|thumb|450px|center|Skala logarytmiczna pozwala lepiej ocenić | |||
różnice pomiędzy czasami wykonania. Prosty program w C jest około dziesięć razy | |||
wolniejszy od kodu korzystającego z LAPACKa i około 50 razy wolniejszy od kodu | |||
korzystającego z LAPACKa i ATLASa.]] | |||
</div></div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
| Linia 217: | Linia 265: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
<div style="font-size:smaller; background-color:#efe"> Wystarczy tylko | <div style="font-size:smaller; background-color:#efe"> Wystarczy tylko <strong>jeden raz</strong> wyznaczyć rozkład LU macierzy <math>\displaystyle A</math> </div> | ||
</div></div> | </div></div> | ||
| Linia 235: | Linia 283: | ||
Rozwiązanie każdego z układów <math>\displaystyle LY = B</math> i <math>\displaystyle UX = Y</math> można przyspieszyć, tworząc | Rozwiązanie każdego z układów <math>\displaystyle LY = B</math> i <math>\displaystyle UX = Y</math> można przyspieszyć, tworząc | ||
warianty | warianty algorytmów podstawienia w przód i w tył, operujące od razu na wszystkich kolumnach macierzy <math>\displaystyle B</math>. Zaimplementowano je w LAPACKu, w tandemie | ||
funkcji <code>DGETRF</code> (rozkład) i <code>DGETRS</code> (rozwiązanie) oraz w | funkcji <code>DGETRF</code> (rozkład) i <code>DGETRS</code> (rozwiązanie) oraz w | ||
<code>DGESV</code>, łączącej funkcjonalność obu. | <code>DGESV</code>, łączącej funkcjonalność obu. | ||
| Linia 246: | Linia 294: | ||
Ważnym przykładem macierzy | Ważnym przykładem macierzy | ||
szczególnej postaci są macierze symetryczne i dodatnio określone. | szczególnej postaci są macierze symetryczne i dodatnio określone. | ||
Są to macierze spełniające | Są to macierze spełniające warunki: | ||
<center><math>\displaystyle x^T A x\,>\,0,\ | <center><math>\displaystyle A=A^T \qquad \mbox{oraz} \qquad x^T A x\,>\,0,\quad\forall x\ne 0. | ||
</math></center> | </math></center> | ||
| Linia 262: | Linia 310: | ||
trójkątną dolną z jedynkami na przekątnej, a <math>\displaystyle D</math> jest macierzą | trójkątną dolną z jedynkami na przekątnej, a <math>\displaystyle D</math> jest macierzą | ||
diagonalną z dodatnimi elementami na diagonali. Opracuj taki algorytm. W jego | diagonalną z dodatnimi elementami na diagonali. Opracuj taki algorytm. W jego | ||
implementacji możesz porównywać się z procedurą LAPACKa <code>DPOSV</code> | implementacji możesz porównywać się z procedurą LAPACKa <code>DPOSV</code>. | ||
Inny wariant tego samego | Inny wariant tego samego | ||
rozkładu to tak zwany rozkład Cholesky'ego--Banachiewicza, w którym przy tych | rozkładu to tak zwany rozkład Cholesky'ego--Banachiewicza, w którym przy tych | ||
| Linia 320: | Linia 368: | ||
macierze <math>\displaystyle A^{(k)}</math> są symetryczne. Pozwala to zmniejszyć --- w stosunku do | macierze <math>\displaystyle A^{(k)}</math> są symetryczne. Pozwala to zmniejszyć --- w stosunku do | ||
rozkładu LU --- koszt | rozkładu LU --- koszt | ||
obliczeniowy o połowę do <math>\displaystyle 2n^3/3</math> operacji arytmetycznych i zmieścić czynniki | obliczeniowy o połowę, do <math>\displaystyle 2n^3/3</math> operacji arytmetycznych i zmieścić czynniki | ||
rozkładu w pamięci przeznaczonej na przechowywanie istotnych elementów <math>\displaystyle A</math> | rozkładu w pamięci przeznaczonej na przechowywanie istotnych elementów <math>\displaystyle A</math> | ||
(czyli w dolnym trójkącie macierzy). | (czyli w dolnym trójkącie macierzy). | ||
| Linia 360: | Linia 408: | ||
<div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | <div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | ||
octave:26> A | octave:26> A=rand(100); | ||
octave:27> det(A) | octave:27> det(A) | ||
ans | ans = -7.5240e+24 | ||
octave:28> det(10*A) | octave:28> det(10*A) | ||
ans | ans = -7.5240e+124 | ||
octave:29> det(100*A) | octave:29> det(100*A) | ||
ans | ans = -7.5240e+224 | ||
octave:30> det(1000*A) | octave:30> det(1000*A) | ||
ans | ans = -Inf | ||
</pre></div> | </pre></div> | ||
| Linia 376: | Linia 424: | ||
octave:32> det(rand(100)) | octave:32> det(rand(100)) | ||
ans | ans = 4.3751e+25 | ||
octave:33> det(rand(400)) | octave:33> det(rand(400)) | ||
ans | ans = -3.0348e+218 | ||
octave:34> det(rand(800)) | octave:34> det(rand(800)) | ||
ans | ans = -Inf | ||
</pre></div> | </pre></div> | ||
Wersja z 16:54, 2 wrz 2006
Ćwiczenia: rozwiązywanie układów równań liniowych
Ćwiczenie: Mnożyć przez odwrotność to nie zawsze to samo...
W Octave układ równań rozwiązujemy korzystając z "operatora rozwiązywania równania"
x = A \ b;
W tym celu Octave oczywiście wewenętrznie wykorzystuje funkcję LAPACKa
DGESV. Ale w Octave jest także funkcja inv, wyznaczająca macierz
odwrotną, więc niektóre (nie najlepsze, oględnie mówiąc) podręczniki zalecają
x = inv(A)*b;
Przedyskutuj, które podejście jest lepsze i dlaczego. Przeprowadź eksperymenty numeryczne weryfikujące Twoją tezę.
Ćwiczenie: Wybór elementu głównego jest naprawdę ważny!
Rozwiąż prosty układ równań
czterema sposobami:
- na kartce papieru (dokładnie!)
- w komputerze, w arytmetyce podwójnej precyzji, korzystając z rozkładu LU bez wyboru elementu głównego
- jak poprzednio, ale z wyborem elementu głównego w kolumnie
- w LAPACKu lub Octave.
Porównaj uzyskane rozwiązania i wyciągnij wnioski.
Ćwiczenie
Zapisz w Octave algorytm rozkładu LU macierzy (bez wyboru elementu głównego) działający in situ.
Wykorzystaj go do napisania funkcji, która rozwiąże układ równań .
Przetestuj tę funkcję na kilku macierzach i porównaj czas jego działania z czasem
wykonania operacji x = A\b.
Spróbuj zastosować swój algorytm do kilku specjalnych macierzy:
- Hilberta dużego wymiaru
- diagonalnej z jednym elementem bardzo małym (a nawet równym zero)
Ćwiczenie: Czy Twoje programy działają naprawdę szybko?
Zrób zadanie poprzednie programując, niczym Zosia-Samosia, wszystko od początku do końca w czystym C. Porównaj czasy działania Twojego programu i programu wywołującego po prostu procedurę biblioteczną LAPACKa
DGESV, najlepiej wspartą dobrze podrasowanymi BLASami.
Ćwiczenie: Układy równań z wieloma prawymi stronami
Podaj sposób taniego wyznaczenia rozwiązania sekwencji układów równań z tą samą macierzą i różnymi prawymi stronami:
Układy równań z tą samą macierzą, ale ze zmieniającą się prawą stroną równania powstają często przy rozwiązywaniu, np. równań różniczkowych cząstkowych, gdzie prawa strona układu odpowiada zmieniającym się warunkom brzegowym.
Ćwiczenie: Metoda Cholesky'ego
Ważnym przykładem macierzy szczególnej postaci są macierze symetryczne i dodatnio określone. Są to macierze spełniające warunki:
Dla takich macierzy można nieco zmniejszyć koszt kombinatoryczny i zużycie pamięci przeprowadzając trochę inny rozkład na macierze trójkątne: tak, aby otrzymać rozkład
zamiast , przy czym jest tu jak zwykle macierzą
trójkątną dolną z jedynkami na przekątnej, a jest macierzą
diagonalną z dodatnimi elementami na diagonali. Opracuj taki algorytm. W jego
implementacji możesz porównywać się z procedurą LAPACKa DPOSV.
Inny wariant tego samego
rozkładu to tak zwany rozkład Cholesky'ego--Banachiewicza, w którym przy tych
samych założeniach na , szukamy rozkładu wykorzystującego tylko jedną macierz
trójkątną dolną:
(oczywiście tym razem nie żądamy, aby miała na diagonali jedynki). Jaka jest relacja między rozkładem a ?
Ćwiczenie: Obliczanie wyznacznika macierzy
Bardzo rzadko w praktyce numerycznej zdarza się potrzeba obliczenia wartości wyznacznika macierzy . Zaproponuj metodę obliczania oraz wskaż, jakiego rodzaju problemy numeryczne możesz napotkać.