TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 103: | Linia 103: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd11.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd11.png]] | ||
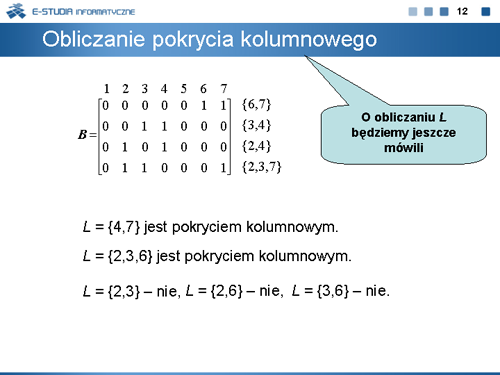
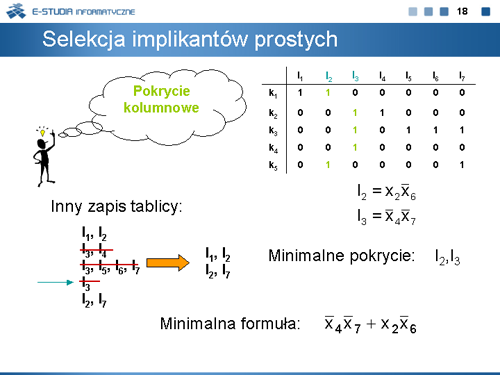
|valign="top"|Pokryciem kolumnowym macierzy <math>B=[b_{ij}]</math>, <math>i\epsilon left \{1,...,w\right \}\,</math>, <math>j\epsilon left \{1,...,n\right \}\,</math> jest zbiór <math>L\subseteq left \{1,...,n\right \}\,</math> taki, że dla każdego <math>i\epsilon left \{1,...,w\right \}\,</math> istnieje <math>j\epsilon L\,</math> , dla którego <math>b_{ij} = 1</math> . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje <math>L' \subseteq L\,</math>, który jest pokryciem macierzy <math>B\,</math>. | |valign="top"|Pokryciem kolumnowym macierzy <math>B=[b_{ij}]</math>, <math>i\epsilon \left \{1,...,w\right \}\,</math>, <math>j\epsilon \left \{1,...,n\right \}\,</math> jest zbiór <math>L\subseteq \left \{1,...,n\right \}\,</math> taki, że dla każdego <math>i\epsilon \left \{1,...,w\right \}\,</math> istnieje <math>j\epsilon L\,</math> , dla którego <math>b_{ij} = 1</math> . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje <math>L' \subseteq L\,</math>, który jest pokryciem macierzy <math>B\,</math>. | ||
|} | |} | ||
| Linia 111: | Linia 111: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd12.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd12.png]] | ||
|valign="top"| | |valign="top"|Obliczenia pokrycia kolumnowego omówimy na przykładzie macierzy blokującej wyznaczonej dla kostki <math>k_2\,</math>. Dla tak obliczonej macierzy <math>B\,</math> , <math>L= \left \{2,3,6\right \}\,</math> (kolumny macierzy B są numerowane od lewej do prawej) jest minimalnym pokryciem kolumnowym. Natomiast <math>L= \left \{2, 3\right \}\,</math> , <math>L= \left \{2,6\right \}\,</math> oraz <math>L= \left \{3,6\right \}\,</math> nie są pokryciami kolumnowymi tej macierzy. | ||
|} | |} | ||
Wersja z 22:44, 28 sie 2006

|
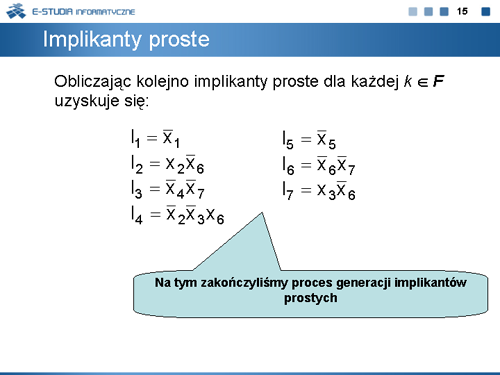
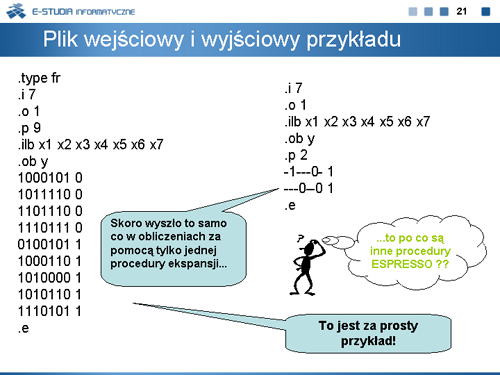
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |

|

|
|

|

|
|
|
|

|