TC Moduł 4

Minimalizacja funkcji boolowskich metodą ekspansji.

---

Kolejną klasyczną metodą minimalizacji funkcji boolowskich jest metoda Quine’a-McCluskey’a . Jest ona wykonywana w dwóch etapach: a) generacji implikantów prostych, b) selekcji minimalnego zbioru implikantów wiernie reprezentującego funkcję $f$. Mimo dużej złożoności obliczeniowej każdego z wyżej wymienionych etapów, metoda Quine’a-McCluskey’a jest najczęściej nauczaną metodą minimalizacji, głównie ze względu na podstawowy charakter jej procedur. Niestety – podobnie jak w przypadku tablic Karnaugha – jest to metoda absolutnie nieprzydatna do algorytmicznych obliczeń komputerowych. Dla potrzeb komputerowych systemów projektowania układów cyfrowych opracowano wiele nowych metod minimalizacji funkcji boolowskich. Najbardziej znaną i uznawaną za najskuteczniejszą jest metoda ESPRESSO opracowana w latach 80. na Uniwersytecie Kalifornijskim w Berkeley.

---

Metoda Espresso polega na iteracyjnym stosowaniu różnych procedur, z których najważniejsze to Ekspansja (Expand), Pokrycie nienadmiarowe (Irredundant Cover) i Uzupełnienie (Complement). Są to bardzo złożone procedury, których omówienie przekracza zakres niniejszego wykładu. Ich pełny opis można znaleźć w książce Brayton R., Hachtel G.D., McMullen C., and Sangiovanni-Vincentelli A.: Logic Minimization Algorithms for VLSI Synthesis. Kluwer Academic Publishers, Boston, 1984 lub w podręczniku Synteza układów logicznych.

---

Najprostszą i najogól¬niejszą procedurą metody ESPRESSO jest procedura Ekspansji. Sama procedura ekspansji wykorzystuje znaną od dawna metodę powiększania mintermu $kϵF$ w taki sposób, aby powiększona kostka nie zawierała żadnego mintermu należącego do zbioru wektorów zerowych funkcji. Ponieważ właściwie powiększony minterm zbioru $F$ może być implikantem funkcji, odpowiednio zmodyfikowana metoda ekspansji może być stosowana autonomicznie jako niezależna metoda minimalizacji funkcji boolowskich. Metoda ta została zrealizowana w programie PANDOR. Program ten jest udostępniony na stronie internetowej www.zpt.tele.pw.edu.pl w katalogu OPROGRAMOWANIE.

---

Pojęciem podstawowym w metodzie ekspansji jest – podobnie jak w innych metodach minimalizacji – pojęcie kostki. Kostkami nazywać będziemy ciągi elementów ze zbioru $\{0,1,*\}$ . Kostki będziemy oznaczać nieindeksowanymi literami, na przykład $k$ , a ich składowe będziemy indeksowali, na przykład $k_i$ . Również, w celu uproszczenia oznaczeń kostki (i wektory) będziemy zapisywać bez przecinków. Na przykład $(*,1,*,0,1)$ zapiszemy jako $(*1*01)$. Kostka to uproszczony zapis zbioru wektorów binarnych. Kostka $K=(0*1*)$ reprezentuje zbiór wektorów: $\begin{array}{c}0010\\ 0011\\ 0110\\ 0111\end{array}$ Kostka reprezentuje również niepełny iloczyn zmiennych binarnych: Na przykład kostkę $K=0*1*$ można zapisać jako ${\bar{x}}_1{x}_3$

---

W metodzie ekspansji podobnie jak w standardzie Espresso zbiór wektorów (w ogólności kostek), dla których funkcja $f=1$ oznacza się $F$. Natomiast zbiór tych wektorów (kostek), dla których funkcja $f=0$ oznacza się $R$.

---

Na planszy przedstawiono tablicę prawdy funkcji boolowskiej 7-argumentowej oraz podano odpowiednie zbiory $F$ i $R$ tej funkcji. Funkcję tę w dalszej części wykładu oznaczać będziemy EXTL. Wektory zbioru $F$ oznaczono symbolami $k_1,...,k_5$ .

---

Ekspansja jest procesem działającym na kostkach zbiorów $F$ i $R$, a jej celem jest uzyskanie dla danej $kϵF$ kostki $k^{\prime }$ tak dużej, jak to tylko możliwe (tzn. z możliwie dużą liczbą pozycji o wartości $*$) i nie pokrywającej żadnego wektora zbioru $R$. W swoich obliczeniach Ekspansja wykorzystuje tzw. macierz blokującą $B$.

---

Macierzą blokującą (kostkę k) nazywać będziemy macierz: $B(k,R)=[b_{ij}]$ , $1\le i\le |R|$ , $1\le j\le n$ w której każdy element $b_{ij}ϵ\{0,1\}$ jest definiowany następująco: $b_{ij}=1$ , jeśli $k_j=1$ oraz $r_{ij}=0$ lub $k_j=0$ oraz $r_{ij}=1$ ; $b_{ij}=0$, w pozostałych przypadkach. W przypadku funkcji opisanej wektorami binarnymi macierz blokująca dla danej kostki $kϵF$ powstaje z macierzy $R$ przez zanegowanie tych kolumn $R$, których pozycje są wyznaczone przez pozycje jedynek w kostce $kϵF$.

---

Wyznaczymy macierz blokującą dla kostki $k_1$ funkcji EXTL z planszy 7. Macierze $F$ i $R$ tej funkcji podane są ponownie na niniejszej planszy. Zgodnie z definicją, skoro $k_1=(0100101)$, to dla uzyskania $B$ wystarczy w macierzy $R$ „zanegować” kolumny drugą, piątą i siódmą, co zaznaczono odpowiednimi kolorami.

---

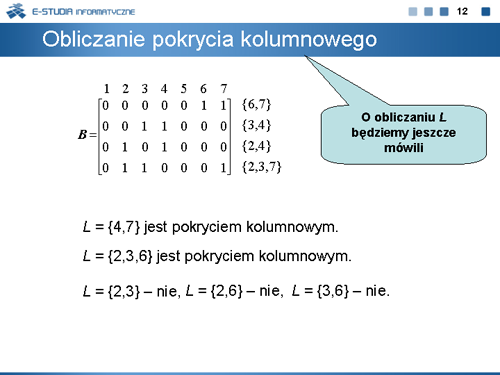
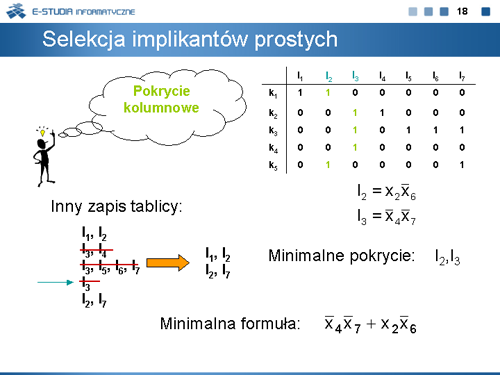
Pokryciem kolumnowym macierzy $B=[b_{ij}]$, Parser nie mógł rozpoznać (błąd składni): {\displaystyle i\epsilon left \{1,...,w\right \}\,} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle j\epsilon left \{1,...,n\right \}\,} jest zbiór Parser nie mógł rozpoznać (błąd składni): {\displaystyle L\subseteq left \{1,...,n\right \}\,} taki, że dla każdego Parser nie mógł rozpoznać (błąd składni): {\displaystyle i\epsilon left \{1,...,w\right \}\,} istnieje $jϵL$ , dla którego $b_{ij}=1$ . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje $L^{\prime }\subseteq L$, który jest pokryciem macierzy $B$.

---

---

---

---

---

---

---

---

---

---

---