TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd1.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd1.png]] | ||
|valign="top"| | |valign="top"|Minimalizacja funkcji boolowskich metodą ekspansji. | ||
|} | |} | ||
| Linia 8: | Linia 9: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd2.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd2.png]] | ||
|valign="top"| | |valign="top"|Kolejną klasyczną metodą minimalizacji funkcji boolowskich jest metoda Quine’a-McCluskey’a . Jest ona wykonywana w dwóch etapach: | ||
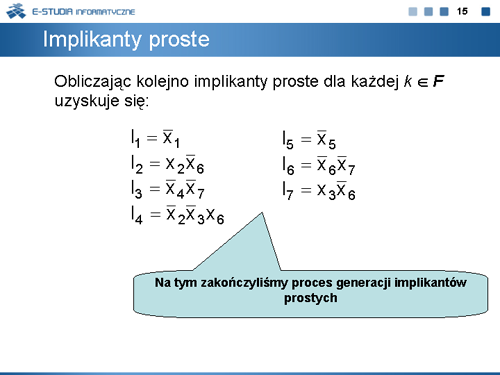
a) generacji implikantów prostych, | |||
b) selekcji minimalnego zbioru implikantów wiernie reprezentującego funkcję <math>f\,</math>. | |||
Mimo dużej złożoności obliczeniowej każdego z wyżej wymienionych etapów, metoda Quine’a-McCluskey’a jest najczęściej nauczaną metodą minimalizacji, głównie ze względu na podstawowy charakter jej procedur. Niestety – podobnie jak w przypadku tablic Karnaugha – jest to metoda absolutnie nieprzydatna do algorytmicznych obliczeń komputerowych. Dla potrzeb komputerowych systemów projektowania układów cyfrowych opracowano wiele nowych metod minimalizacji funkcji boolowskich. Najbardziej znaną i uznawaną za najskuteczniejszą jest metoda ESPRESSO opracowana w latach 80. na Uniwersytecie Kalifornijskim w Berkeley. | |||
|} | |} | ||
| Linia 15: | Linia 23: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd3.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd3.png]] | ||
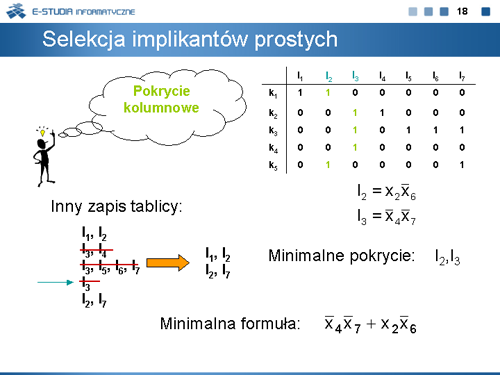
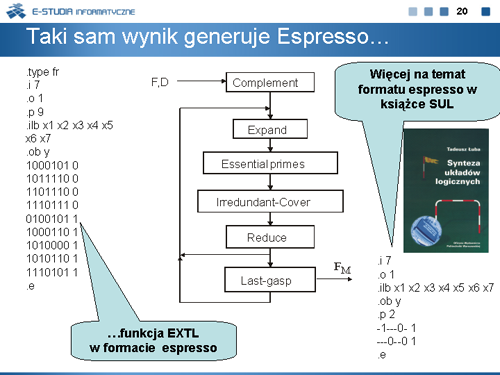
|valign="top"| | |valign="top"|Metoda Espresso polega na iteracyjnym stosowaniu różnych procedur, z których najważniejsze to Ekspansja (Expand), Pokrycie nienadmiarowe (''Irredundant Cover'') i Uzupełnienie (''Complement''). Są to bardzo złożone procedury, których omówienie przekracza zakres niniejszego wykładu. Ich pełny opis można znaleźć w książce Brayton R., Hachtel G.D., McMullen C., and Sangiovanni-Vincentelli A.: ''Logic Minimization Algorithms for VLSI Synthesis''. Kluwer Academic Publishers, Boston, 1984 lub w podręczniku ''Synteza układów logicznych''. | ||
|} | |} | ||
| Linia 22: | Linia 31: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd4.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd4.png]] | ||
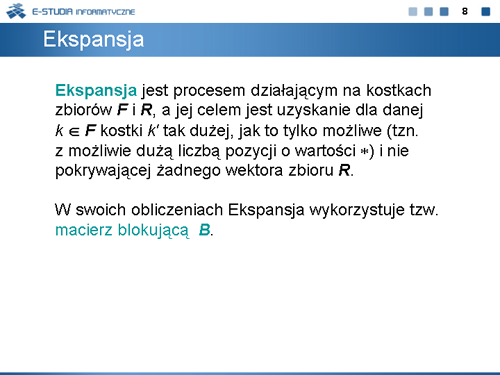
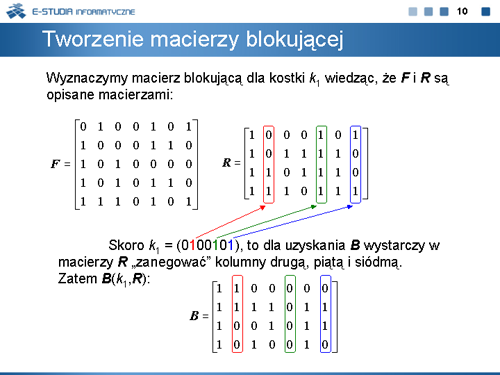
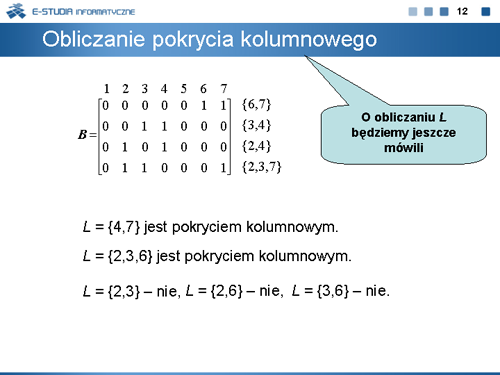
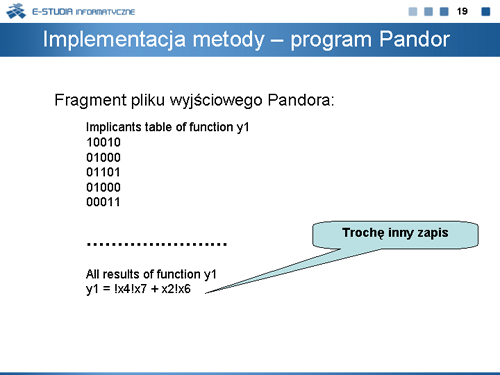
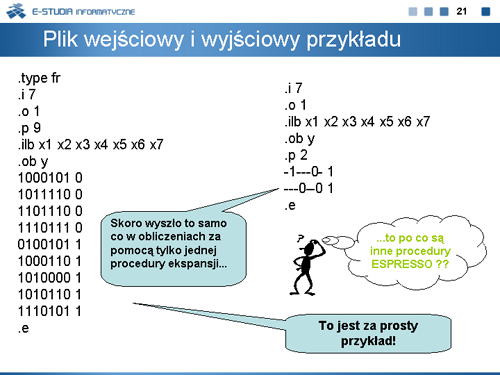
|valign="top"| | |valign="top"|Najprostszą i najogól¬niejszą procedurą metody ESPRESSO jest procedura Ekspansji. Sama procedura ekspansji wykorzystuje znaną od dawna metodę powiększania mintermu <math>k \epsilon F\,</math> w taki sposób, aby powiększona kostka nie zawierała żadnego mintermu należącego do zbioru wektorów zerowych funkcji. Ponieważ właściwie powiększony minterm zbioru <math>F\,</math> może być implikantem funkcji, odpowiednio zmodyfikowana metoda ekspansji może być stosowana autonomicznie jako niezależna metoda minimalizacji funkcji boolowskich. Metoda ta została zrealizowana w programie PANDOR. Program ten jest udostępniony na stronie internetowej www.zpt.tele.pw.edu.pl w katalogu OPROGRAMOWANIE. | ||
|} | |} | ||
| Linia 29: | Linia 39: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd5.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd5.png]] | ||
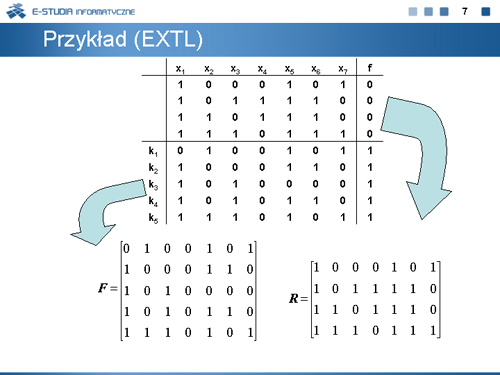
|valign="top"| | |valign="top"|Pojęciem podstawowym w metodzie ekspansji jest – podobnie jak w innych metodach minimalizacji – pojęcie kostki. Kostkami nazywać będziemy ciągi elementów ze zbioru <math>\left \{0, 1, *\right \}</math> . Kostki będziemy oznaczać nieindeksowanymi literami, na przykład <math>k\,</math> , a ich składowe będziemy indeksowali, na przykład <math>k_i\,</math> . Również, w celu uproszczenia oznaczeń kostki (i wektory) będziemy zapisywać bez przecinków. Na przykład <math>(*,1,*,0,1)\,</math> zapiszemy jako <math>(*1*01)\,</math>. | ||
Kostka to uproszczony zapis zbioru wektorów binarnych. Kostka <math>K=(0*1*)</math> reprezentuje zbiór wektorów: | |||
:<math>\begin{matrix} 0010 \\ 0011 \\ 0110 \\ 0111 \end{matrix}</math> | |||
Kostka reprezentuje również niepełny iloczyn zmiennych binarnych: Na przykład kostkę <math>K=0*1*</math> można zapisać jako <math>\overline{x}_1x_3\,</math> | |||
|} | |} | ||
Wersja z 22:13, 28 sie 2006

|
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
|
|

|
|

|
|

|

|
|

|

|
|
|
|

|



