PS Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
|valign="top"| | |valign="top"| | ||
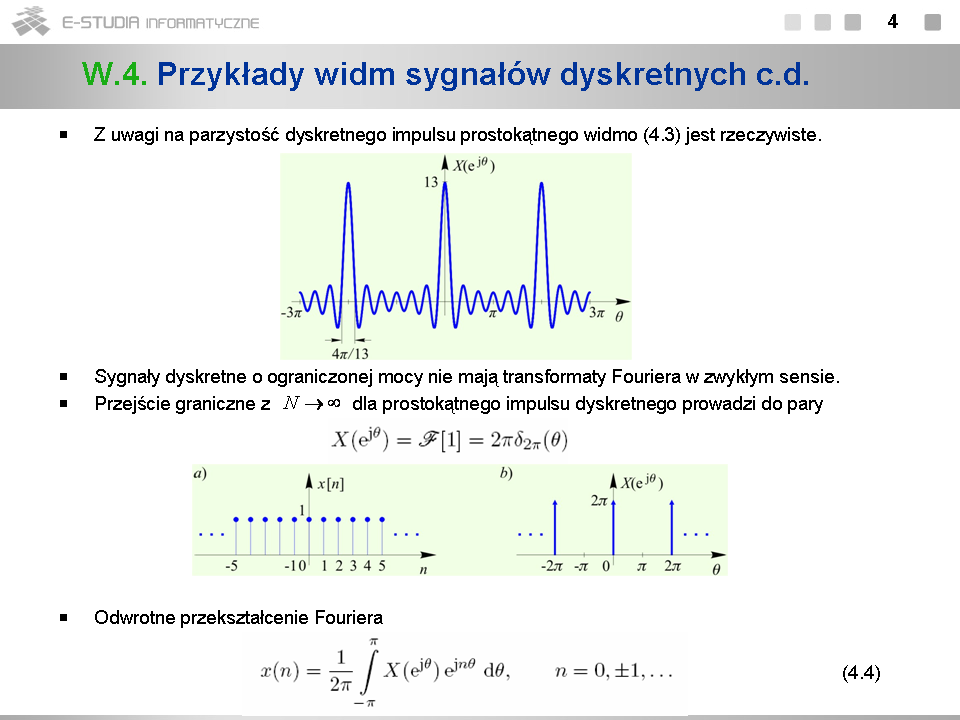
*Okresowość widm sygnałów dyskretnych jest ich podstawową cechą. Gdybyśmy widma te wyrazili w funkcji częstotliwości <math>f=\omega/2\pi</math> , ich okres byłby równy częstotliwości próbkowania <math>f_s\,</math> . | *Okresowość widm sygnałów dyskretnych jest ich podstawową cechą. Gdybyśmy widma te wyrazili w funkcji częstotliwości <math>f=\omega/2\pi</math> , ich okres byłby równy częstotliwości próbkowania <math>f_s\,</math> . | ||
*Jeśli widmo sygnału dyskretnego jest wyrażone w funkcji pulsacji unormowanej <math>\theta=\omega/2\pi</math> , jego okres jest równy <math>\pi\,</math> . | *Jeśli widmo sygnału dyskretnego jest wyrażone w funkcji pulsacji unormowanej <math>\theta=\omega/2\pi</math> , jego okres jest równy <math>2\pi\,</math> . | ||
*Widmo (4.2) można także zapisać w funkcji częstotliwości unormowanej <math>\nu=\omega/{\omega_s}=f/f_s=\theta/2\pi</math> . Jego okres jest wówczas równy <math>1\,</math>. | *Widmo (4.2) można także zapisać w funkcji częstotliwości unormowanej <math>\nu=\omega/{\omega_s}=f/f_s=\theta/2\pi</math> . Jego okres jest wówczas równy <math>1\,</math>. | ||
Wersja z 02:38, 26 sie 2006

|

|
|

|

|

|

|
|