PS Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 36: | Linia 36: | ||
|valign="top"| | |valign="top"| | ||
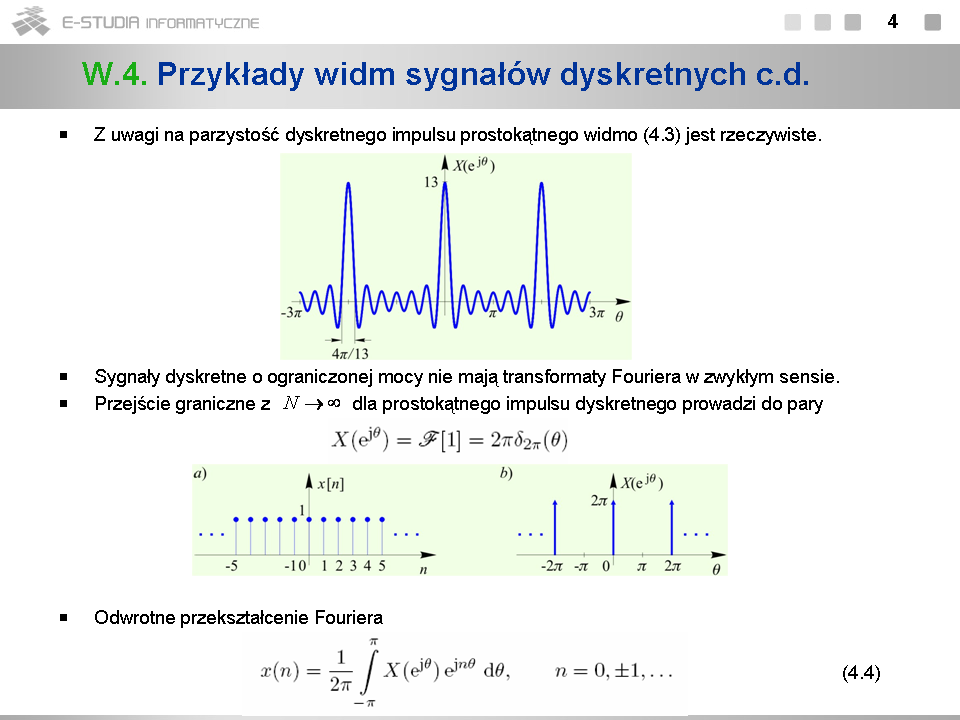
*Wykres widma amplitudowego dyskretnego impulsu prostokątnego został sporządzony dla <math>N=6\,</math> w przedziale <math>[-3\pi, 3\pi]\,</math> . Jeśli <math>N\,</math> rośnie, wysokość okresowo powtarzanych „listków” głównych widma rośnie, a ich szerokość maleje. Jednocześnie maleje poziom listków bocznych. | *Wykres widma amplitudowego dyskretnego impulsu prostokątnego został sporządzony dla <math>N=6\,</math> w przedziale <math>[-3\pi, 3\pi]\,</math> . Jeśli <math>N\,</math> rośnie, wysokość okresowo powtarzanych „listków” głównych widma rośnie, a ich szerokość maleje. Jednocześnie maleje poziom listków bocznych. | ||
*Zwiększając <math>N\,</math> | *Zwiększając <math>N\,</math> do nieskończoności otrzymujemy w granicy dyskretny sygnał stały. Przejściu granicznemu towarzyszy wzrost wysokości listków głównych widma do nieskończoności i zanikanie listków bocznych do zera. W efekcie otrzymujemy dystrybucję grzebieniową w dziedzinie częstotliwości (rys. b) | ||
*Wzór (4.4) określa wartości kolejnych próbek sygnału dla <math>n \epsilon \Box\,</math> . | *Wzór (4.4) określa wartości kolejnych próbek sygnału dla <math>n \epsilon \Box\,</math> . | ||
| Linia 46: | Linia 46: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd5.png]] | ||
|valign="top"| | |valign="top"| | ||
*Twierdzenia dotyczące przekształcenia Fouriera sygnałów dyskretnych mają swoje ścisłe odpowiedniki w twierdzeniach dotyczących przekształcenia Fouriera sygnałów analogowych. Podobna też jest ich interpretacja. | |||
|} | |} | ||
| Linia 54: | Linia 55: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
*Uogólnione twierdzenie Rayleigha wyraża równość iloczynów skalarnych w przestrzeni <math>l^2\,</math> sygnałów dyskretnych i przestrzeni <math>{L^2}_{2\pi}\,</math> ich okresowych widm. | |||
*Twierdzenie Parsevala wyraża równość norm w obu tych przestrzeniach. | |||
|} | |} | ||
| Linia 62: | Linia 65: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd7.png]] | ||
|valign="top"| | |valign="top"| | ||
*Sygnały <math>N\,</math>-okresowe są szczególnym przypadkiem sygnałów dyskretnych. Powstają one np. w wyniku próbkowania okresowych sygnałów analogowych dokładnie <math>N\,</math> razy w okresie. | |||
*W celu podkreślenia <math>N\,</math>-okresowości sygnałów są one oznaczane z kreską u góry. | |||
*Sygnały bazowe w przestrzeni Hilberta pełnią podobną rolę jak sygnały bazowe w przestrzeni Hilberta , . Zasadnicza różnica polega jednak na tym, że w przypadku przestrzeni baza jest skończona. | |||
|} | |} | ||
Wersja z 16:48, 25 sie 2006

|

|
|

|

|

|

|
|