PS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd1.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę ''metod częstotliwościowych'' lub ''metod widmowych''. | *Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę ''metod częstotliwościowych'' lub ''metod widmowych''. | ||
| Linia 11: | Linia 11: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd2.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału <math>x(t)=X_0\Pi(t/T)</math> . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. | *Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału <math>x(t)=X_0\Pi(t/T)</math> . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. | ||
| Linia 22: | Linia 22: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd3.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
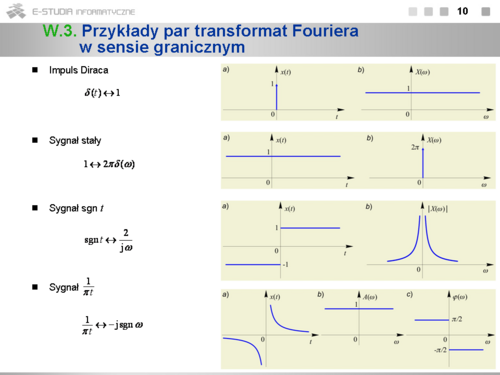
*Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. | *Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. | ||
| Linia 31: | Linia 31: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej <math>\omega\,</math> i mają wyraźną interpretację fizyczną. | *Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej <math>\omega\,</math> i mają wyraźną interpretację fizyczną. | ||
| Linia 41: | Linia 41: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji <math>|\omega|<2\pi /T</math> obejmuje tzw. ''listek główny'', a po obu jego stronach występują ''listki boczne''. | *Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji <math>|\omega|<2\pi /T</math> obejmuje tzw. ''listek główny'', a po obu jego stronach występują ''listki boczne''. | ||
| Linia 51: | Linia 51: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej <math>\omega\,</math> . Widmo tych sygnałów jest zatem ''funkcją hermitowską'', tj. <math>X(\omega)=X^{*}(-\omega)</math> . | *Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej <math>\omega\,</math> . Widmo tych sygnałów jest zatem ''funkcją hermitowską'', tj. <math>X(\omega)=X^{*}(-\omega)</math> . | ||
| Linia 67: | Linia 67: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Różniczkowaniu sygnału w dziedzinie czasu odpowiada mnożenie jego widma przez <math>j\omega\,</math> w dziedzinie częstotliwości. | *Różniczkowaniu sygnału w dziedzinie czasu odpowiada mnożenie jego widma przez <math>j\omega\,</math> w dziedzinie częstotliwości. | ||
| Linia 80: | Linia 80: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd8.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Ponieważ sygnał wykładniczy obustronny jest parzysty jego widmo jest rzeczywiste i parzyste. Jak widać, jest to sygnał dolnopasmowy. Parę tę można bez trudu wyprowadzić wprost z definicji przekształcenia Fouriera. | *Ponieważ sygnał wykładniczy obustronny jest parzysty jego widmo jest rzeczywiste i parzyste. Jak widać, jest to sygnał dolnopasmowy. Parę tę można bez trudu wyprowadzić wprost z definicji przekształcenia Fouriera. | ||
| Linia 92: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd9.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo sygnału Gaussa ma również kształt krzywej Gaussa. Jest to jedna z nielicznych par transformat Fouriera o tej właściwości | *Widmo sygnału Gaussa ma również kształt krzywej Gaussa. Jest to jedna z nielicznych par transformat Fouriera o tej właściwości | ||
| Linia 102: | Linia 102: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd10.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo impulsu Diraca jest stałe w całym przedziale pulsacji. Widmo takie nazywamy ''białym''. | *Widmo impulsu Diraca jest stałe w całym przedziale pulsacji. Widmo takie nazywamy ''białym''. | ||
| Linia 113: | Linia 113: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd11.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
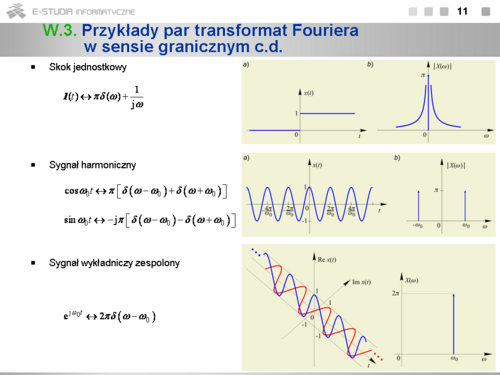
*Widmo skoku jednostkowego można wyznaczyć, przedstawiając go w postaci <math>1(t)=1/2+(sgn\, t)/2</math> i korzystając z poprzednio omówionych par. | *Widmo skoku jednostkowego można wyznaczyć, przedstawiając go w postaci <math>1(t)=1/2+(sgn\, t)/2</math> i korzystając z poprzednio omówionych par. | ||
| Linia 123: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0) </math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\,</math> , <math>k=0,\pm\ 1,...\,</math> , co oddaje jego dyskretny charakter. | *Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0) </math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\,</math> , <math>k=0,\pm\ 1,...\,</math> , co oddaje jego dyskretny charakter. | ||
| Linia 134: | Linia 134: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd13.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd13.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo unipolarnej fali prostokątnej wykreślono dla dwóch różnych wartości okresu fali <math>T_0\,</math> i stałej szerokości impulsu <math>T\,</math> . W miarę zwiększania okresu prążki zagęszczają się i ich wysokości maleją. Nie zmieniają się natomiast miejsca zerowe obwiedni, które zależą tylko od szerokości impulsu <math>T\,</math> . | *Widmo unipolarnej fali prostokątnej wykreślono dla dwóch różnych wartości okresu fali <math>T_0\,</math> i stałej szerokości impulsu <math>T\,</math> . W miarę zwiększania okresu prążki zagęszczają się i ich wysokości maleją. Nie zmieniają się natomiast miejsca zerowe obwiedni, które zależą tylko od szerokości impulsu <math>T\,</math> . | ||
| Linia 143: | Linia 143: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd14.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
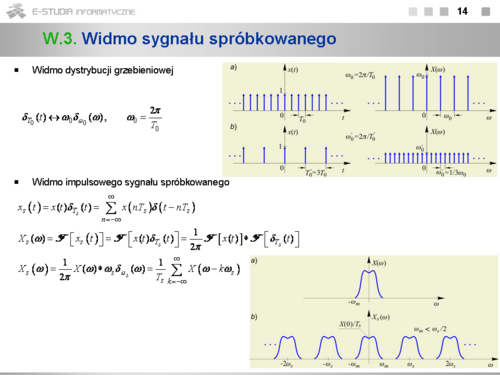
*Widmo w sensie granicznym dystrybucji grzebieniowej <math>\delta_{T_0}(t)</math> o okresie <math>T_0\,</math> jest również dystrybucją grzebieniową <math>\omega_0 \delta_{\omega_0}(\omega)\,</math> o okresie <math>\omega_0=2\pi/T_0</math> i jednakowych polach impulsów widmowych równych <math>\omega_0\,</math> . Wynika to z faktu, co można łatwo pokazać wykonując odpowiednie obliczenie, że współczynniki rozwinięcia dystrybucji <math>\delta_{T_0}(t)</math> w zespolony szereg Fouriera są identyczne dla każdego <math>k\,</math> i równe <math>X_k=1/T_0</math> . | *Widmo w sensie granicznym dystrybucji grzebieniowej <math>\delta_{T_0}(t)</math> o okresie <math>T_0\,</math> jest również dystrybucją grzebieniową <math>\omega_0 \delta_{\omega_0}(\omega)\,</math> o okresie <math>\omega_0=2\pi/T_0</math> i jednakowych polach impulsów widmowych równych <math>\omega_0\,</math> . Wynika to z faktu, co można łatwo pokazać wykonując odpowiednie obliczenie, że współczynniki rozwinięcia dystrybucji <math>\delta_{T_0}(t)</math> w zespolony szereg Fouriera są identyczne dla każdego <math>k\,</math> i równe <math>X_k=1/T_0</math> . | ||
| Linia 153: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd15.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Szereg Fouriera można traktować jako szczególny przypadek przekształcenia Fouriera sygnałów okresowych w sensie granicznym. | *Szereg Fouriera można traktować jako szczególny przypadek przekształcenia Fouriera sygnałów okresowych w sensie granicznym. | ||
| Linia 163: | Linia 163: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd16.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd16.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*W teorii obwodów obowiązuje zasada, że im czas trwania sygnału jest krótszy (im impuls jest węższy), tym jego widmo jest szersze. | *W teorii obwodów obowiązuje zasada, że im czas trwania sygnału jest krótszy (im impuls jest węższy), tym jego widmo jest szersze. | ||