PS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 9: | Linia 9: | ||
**określenie kąta między sygnałami, w szczególności rozstrzyganie ich ortogonalności (analogicznie jak na podstawie iloczynu skalarnego można wnioskować o prostopadłości wektorów w przestrzeni <math>\Box^n\,</math> ). | **określenie kąta między sygnałami, w szczególności rozstrzyganie ich ortogonalności (analogicznie jak na podstawie iloczynu skalarnego można wnioskować o prostopadłości wektorów w przestrzeni <math>\Box^n\,</math> ). | ||
*Korzystanie z analogii między dobrze znaną zwykłą przestrzenią wektorową <math>\Box^n\,</math> (aczkolwiek jest to skończenie wymiarowa przestrzeń Hilberta) a przestrzeniami sygnałowymi Hilberta (które najczęściej, choć nie zawsze, są przestrzeniami nieskończenie wymiarowymi) znakomicie ułatwia zrozumienie pojęć tej części wykładu. Z uwagi na tę analogię metody analizy i syntezy sygnałów oparte na ich reprezentacjach w przestrzeniach Hilberta noszą nazwę ''metod geometrycznych''. | *Korzystanie z analogii między dobrze znaną zwykłą przestrzenią wektorową <math>\Box^n\,</math> (aczkolwiek jest to skończenie wymiarowa przestrzeń Hilberta) a przestrzeniami sygnałowymi Hilberta (które najczęściej, choć nie zawsze, są przestrzeniami nieskończenie wymiarowymi) znakomicie ułatwia zrozumienie pojęć tej części wykładu. Z uwagi na tę analogię metody analizy i syntezy sygnałów oparte na ich reprezentacjach w przestrzeniach Hilberta noszą nazwę ''metod geometrycznych''. | ||
|} | |} | ||
| Linia 94: | Linia 96: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
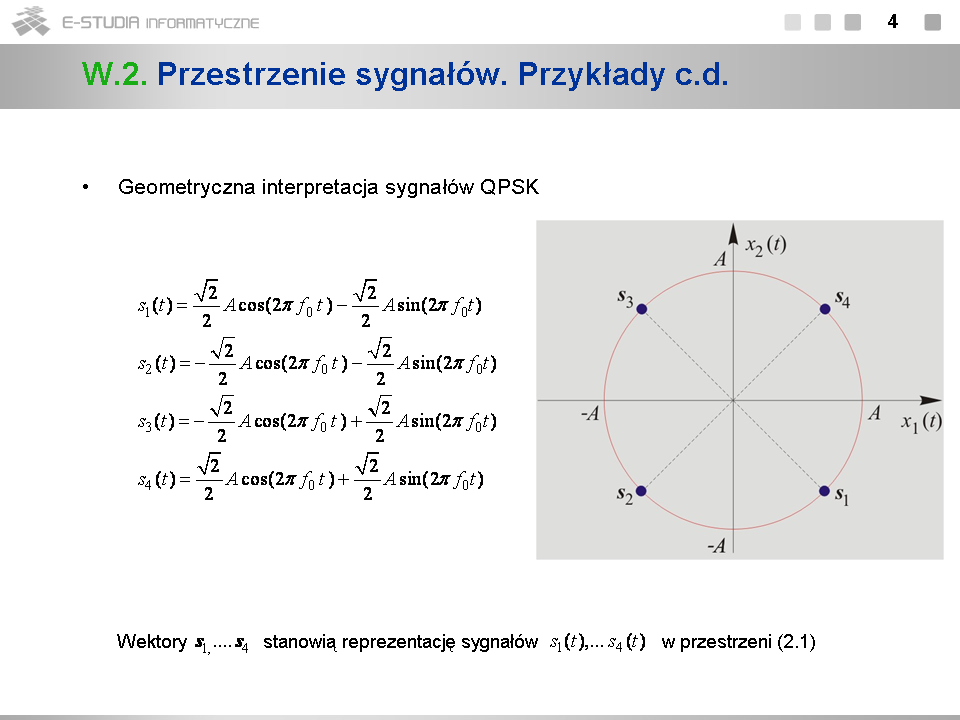
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd9.png]] | |width="500px" valign="top"|[[Grafika:PS_M2_Slajd9.png]] | ||
|valign="top"| | |valign="top"| | ||
*Przestrzeniami Hilberta są także przestrzenie <math>L^2(0,\, \infty)\,</math> oraz <math>L^2(-\infty,\, \infty)\,</math> . | |||
*W przestrzeni sygnałów nieokresowych o ograniczonej mocy nie można w ogólnym przypadku wprowadzić iloczynu skalarnego. Dla przestrzeni tej można natomiast zdefiniować pseudoiloczyn skalarny o zbliżonych właściwościach formalnych. | |||
*Przestrzeniami Hilberta są oczywiście również zbiory wszystkich sygnałów dyskretnych o ograniczonej energii określonych dla <math>n\epsilon\Box\,</math> oraz dla <math>n\epsilon [n_1,\, n_2]\,</math> . W tym ostatnim przypadku przestrzeń jest tożsama ze zwykłą przestrzenią wektorową o wymiarze <math>n_2-n_1+1\,</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd10.png]] | |||
|valign="top"| | |||
*Baza <math>\left \{x_k :\, k\epsilon K\right \}</math> danej przestrzeni może być skończona, gdy zbiór indeksów <math>K\,</math> jest skończony, lub nieskończona, gdy zbiór <math>K\,</math> jest przeliczalny (z reguły równy <math>\Box\cup\left \{0\right \}</math> lub <math>\Box\,</math> ) | |||
*Przestrzeń rozpięta na bazie danej przestrzeni może być identyczna z tą przestrzenią lub być jej podprzestrzenią. | |||
*Nie w każdej przestrzeni Hilberta istnieje baza ortogonalna. Przestrzeń Hilberta, w której można wyróżnić taką bazę nosi nazwę ''ośrodkowej przestrzeni'' Hilberta. W ogólnym przypadku w danej przestrzeni Hilberta może istnieć więcej niż jedna baza ortogonalna. | |||
*Sygnały ortonormalne są wiernym odpowiednikiem wersorów w zwykłej przestrzeni wektorowej. | |||
*Każdą bazę przestrzeni Hilberta (a więc zbiór elementów liniowo niezależnych) można zortogonalizować i unormować stosując znaną w literaturze ''procedurę ortonormalizacji Grama-Schmidta''. | |||