PS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 29: | Linia 29: | ||
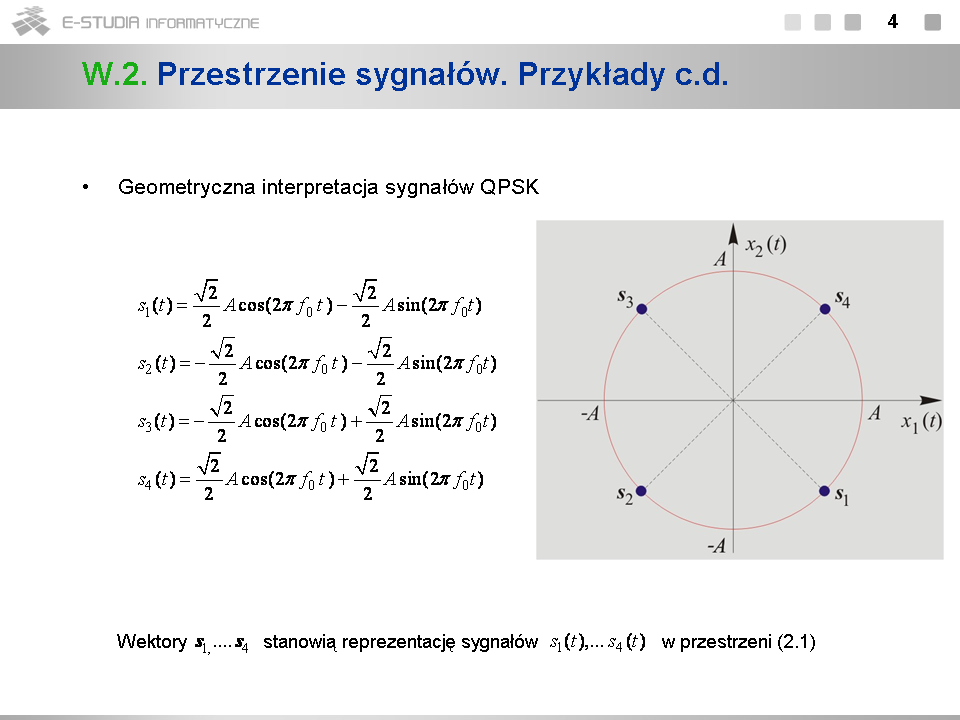
*W systemie czterowartościowej modulacji cyfrowej QPSK informacja jest transmitowana w postaci ciągu prostokątnych impulsów radiowych o jednakowym czasie trwania <math>T\,</math> , jednakowej częstotliwości <math>f_0=1/T\,</math> i amplitudzie <math>A\,</math> oraz różnych losowych fazach. W każdym przedziale czasu o długości <math>T\,</math> transmitowany jest jeden z impulsów <math>s_1(t),\, s_2(t),\, s_3(t),\,</math> lub <math>s_4(t)\,</math> . | *W systemie czterowartościowej modulacji cyfrowej QPSK informacja jest transmitowana w postaci ciągu prostokątnych impulsów radiowych o jednakowym czasie trwania <math>T\,</math> , jednakowej częstotliwości <math>f_0=1/T\,</math> i amplitudzie <math>A\,</math> oraz różnych losowych fazach. W każdym przedziale czasu o długości <math>T\,</math> transmitowany jest jeden z impulsów <math>s_1(t),\, s_2(t),\, s_3(t),\,</math> lub <math>s_4(t)\,</math> . | ||
*Informacja jest zakodowana w fazie, przy czym cztery możliwe wartości fazy odpowiadają transmitowanym dwubitom: „10”, „00”, „01” oraz „11”. Z reguły <math>T_0\, \Box\, T\,</math> , a ponadto <math>T/T_0\,</math> jest liczbą całkowitą, tzn. na przedział <math>T\,</math> przypada całkowita liczba okresów fali harmonicznej. | *Informacja jest zakodowana w fazie, przy czym cztery możliwe wartości fazy odpowiadają transmitowanym dwubitom: „10”, „00”, „01” oraz „11”. Z reguły <math>T_0\, \Box\, T\,</math> , a ponadto <math>T/T_0\,</math> jest liczbą całkowitą, tzn. na przedział <math>T\,</math> przypada całkowita liczba okresów fali harmonicznej. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd4.png]] | |||
|valign="top"| | |||
*Korzystając z elementarnych tożsamości trygonometrycznych sygnały QPSK można doprowadzić do postaci (2.1). Otrzymane współczynniki <math>a\,</math> i <math>b\,</math> przy składowych bazowych <math>cos\, 2\pi f_0 t\,</math> i <math>sin\, 2\pi f_0 t\,</math> są zarazem współrzędnymi wektorów reprezentujących sygnały QPSK. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd5.png]] | |||
|valign="top"| | |||
*Pojęcie przestrzeni metrycznej jest podstawowym pojęciem analizy funkcjonalnej. | |||
*W danym zbiorze można określić więcej niż jedną metrykę. Ten sam zbiór z dwiema różnymi metrykami stanowi dwie różne przestrzenie metryczne. | |||
*Dla prostoty zapisu w definicjach metryk przestrzeni <math>L^2(0,\, T)\,</math> i <math>{L^2}_{T_0}\,</math> opuszczony został argument <math>t\,</math> w zapisach sygnałów. | |||
*Analogicznie można zdefiniować przestrzenie metryczne <math>L^2(0,\, \infty)\,</math> oraz <math>L^2(-\infty,\, \infty)\,</math> sygnałów o ograniczonej energii określonych w przedziale <math>[0,\, \infty)\,</math> i odpowiednio <math>(-\infty,\, \infty)\,</math> , zmieniając w definicji metryki granice całkowania. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd6.png]] | |||
|valign="top"| | |||
*Metryka opisuje właściwości geometryczne zbioru <math>X\,</math> . W przestrzeni liniowej są natomiast określone dodatkowo operacje na jej elementach, a przez to konkretna struktura algebraiczna. | |||
*W zastosowaniach teorii sygnałów ciałem <math>F\,</math> jest zwykle albo zbiór liczb rzeczywistych <math>\Box\,</math> albo zespolonych <math>\Box\,</math> (zakładamy tu, że pojęcie ciała jest znane). | |||
*W zapisie aksjomatów 1-6 pomijany jest dla prostoty znak operacji mnożenia <math>"\cdot"\,</math>. | |||
*Z aksjomatów przestrzeni liniowej wynikają następujące oczywiste właściwości: | |||
**<math>x+\varnothing=x</math> , | |||
**istnieje jedyny element <math>-x\epsilon X</math> , taki że <math>x+(-x)=\varnothing</math> , | |||
**jeśli <math>\alpha x=\varnothing</math> i <math>x\neq\varnothing</math> , to <math>\alpha=0</math> . | |||