PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 163: | Linia 163: | ||
*Sygnałami harmonicznymi zespolonymi posługujemy się również w innych reprezentacjach sygnałów rzeczywistych, np. zbiór sygnałów <math>\left \{e^{jk\omega_0 t} : k\epsilon\Box\right \}\,</math> tworzy tzw. ''bazę'' rozwinięcia sygnału okresowego o okresie <math>T_0=2\pi/{\omega_0}</math> w zespolony szereg Fouriera (por. wzór (1.2)). | *Sygnałami harmonicznymi zespolonymi posługujemy się również w innych reprezentacjach sygnałów rzeczywistych, np. zbiór sygnałów <math>\left \{e^{jk\omega_0 t} : k\epsilon\Box\right \}\,</math> tworzy tzw. ''bazę'' rozwinięcia sygnału okresowego o okresie <math>T_0=2\pi/{\omega_0}</math> w zespolony szereg Fouriera (por. wzór (1.2)). | ||
*Pojęcie ''sygnału analitycznego'', określonego wzorami (1.12) i (1.13), jest jednym z ważniejszych pojęć teorii sygnałów. Stanowi on uogólnienie na sygnały nieharmoniczne reprezentacji rzeczywistego sygnału harmonicznego <math>cos\omega_0 t\,</math> zespolonym sygnałem harmonicznym <math>e^{j\omega_0 t}=cos\omega_0 t+jsin\omega_0 t</math> . Zgodnie z definicją sygnał <math>e^{j\omega_0 t}\,</math> jest właśnie sygnałem analitycznym sygnału <math>\omega_0 t\,</math> . | *Pojęcie ''sygnału analitycznego'', określonego wzorami (1.12) i (1.13), jest jednym z ważniejszych pojęć teorii sygnałów. Stanowi on uogólnienie na sygnały nieharmoniczne reprezentacji rzeczywistego sygnału harmonicznego <math>cos\omega_0 t\,</math> zespolonym sygnałem harmonicznym <math>e^{j\omega_0 t}=cos\omega_0 t+jsin\omega_0 t</math> . Zgodnie z definicją sygnał <math>e^{j\omega_0 t}\,</math> jest właśnie sygnałem analitycznym sygnału <math>\omega_0 t\,</math> . | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
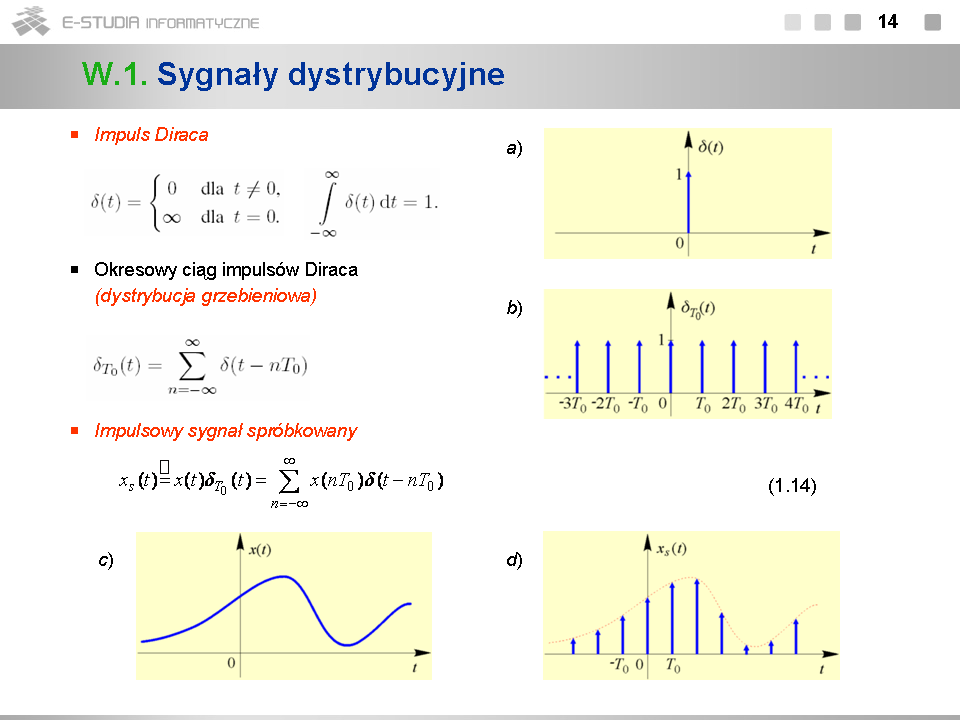
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd14.png]] | |||
|valign="top"| | |||
*''Impuls Diraca <math>\delta(t)</math>'' (rys. a), nazywany również ''dystrybucją'' lub ''deltą Diraca'', jest matematycznym modelem nierealizowalnego fizycznie, nieskończenie wąskiego impulsu występującego w chwili <math>t=0\,</math> , o nieskończenie dużej amplitudzie i polu równym <math>1\,</math>. Z formalnego punktu widzenia jest to sygnał o nieograniczonej mocy! Zapis <math>X_0\delta (t-t_0)\,</math> oznacza impuls Diraca występujący w chwili <math>t_0\,</math> o polu równym <math>X_0\,</math> . | |||
*Przytoczona definicja impulsu <math>\delta(t)</math> jest definicją klasyczną, podaną jeszcze przez Diraca. Współcześnie deltę Diraca definiuje się w sposób bardziej ścisły na gruncie ''teorii dystrybucji''. | |||
*Za pomocą dystrybucji grzebieniowej (nazywanej w literaturze także dystrybucją ''sza'' lub ''comb'') można w sposób wygodny zapisać formalnie operację próbkowania równomiernego sygnału jako iloczyn tego sygnału i dystrybucji <math>\delta_{T_0}\,</math> . W efekcie otrzymujemy tzw. ''impulsowy sygnał spróbkowany'' (1.14) pokazany na rys. d). Sygnał ten stanowi dystrybucyjną reprezentację sygnału spróbkowanego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd15.png]] | |||
|valign="top"| | |||
*Zgodnie z właściwością (1.15), w wyniku mnożenia sygnału <math>x(t)\,</math> przez impuls Diraca <math>\delta(t-t_0)\,</math> występujący w chwili <math>t_0\,</math> wyodrębniamy niejako z całego sygnału <math>x(t)\,</math> jego wartość (próbkę) <math>x(t_0)\,</math> w chwili <math>t_0\,</math> , którą reprezentujemy impulsem Diraca <math>\delta(t-t_0)\,</math> o polu równym <math>x(t_0)\,</math> . Inaczej mówiąc, impuls <math>x(t_0)\delta(t-t_0)\,</math> stanowi reprezentację dystrybucyjną próbki <math>x(t_0)\,</math> . | |||
*Właściwość filtracji (1.16) wynika natychmiast w właściwości (1.15) i definicji dystrybucji Diraca. | |||
*Całka impulsu Diraca w granicach od <math>-\infty\,</math> do <math>t\,</math> jest równa sygnałowi skoku jednostkowego. Pochodna skoku jednostkowego jest równa impulsowi Diraca. Związki te należy jednak rozumieć w sensie dystrybucyjnym. | |||
*Splot sygnału <math>x(t)\,</math> z impulsem Diraca <math>\delta(t)\,</math> daje w wyniku ponownie sygnał <math>x(t)\,</math> . Oznacza to, że <math>\delta(t)\,</math> jest elementem identycznościowym operacji splotu. Splot sygnału <math>x(t)\,</math> z impulsem Diraca przesuniętym o czas <math>t_0\,</math> daje w wyniku niezmienioną kopię tego sygnału przesuniętą o ten sam czas. | |||