PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 161: | Linia 161: | ||
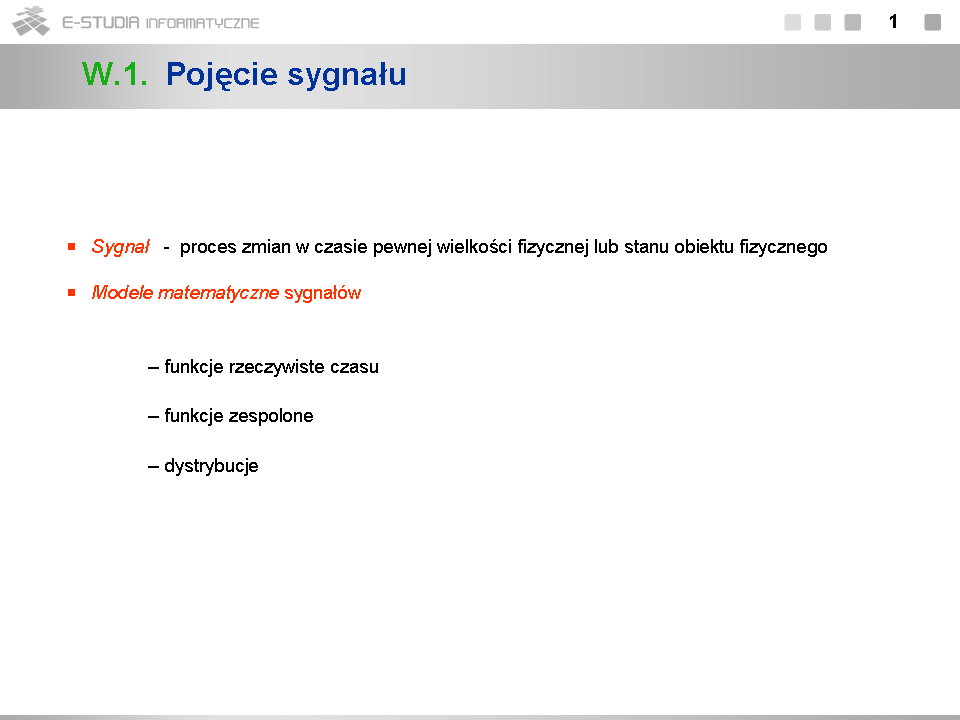
*''Sygnał harmoniczny zespolony'' <math>z(t)=e^{j\omega_0 t}</math> (1.11), nazywany także sinusoidą zespoloną, jest często wykorzystywany do reprezentacji rzeczywistego sygnału harmonicznego <math>x(t)=cos\omega_0 t</math> , przy czym <math>x(t)=Re\, z(t)</math> . Jest to oczywiście sygnał o ograniczonej mocy. Jego moc, jak można łatwo sprawdzić korzystając ze zmodyfikowanego wzoru (1.8), jest równa 1. | *''Sygnał harmoniczny zespolony'' <math>z(t)=e^{j\omega_0 t}</math> (1.11), nazywany także sinusoidą zespoloną, jest często wykorzystywany do reprezentacji rzeczywistego sygnału harmonicznego <math>x(t)=cos\omega_0 t</math> , przy czym <math>x(t)=Re\, z(t)</math> . Jest to oczywiście sygnał o ograniczonej mocy. Jego moc, jak można łatwo sprawdzić korzystając ze zmodyfikowanego wzoru (1.8), jest równa 1. | ||
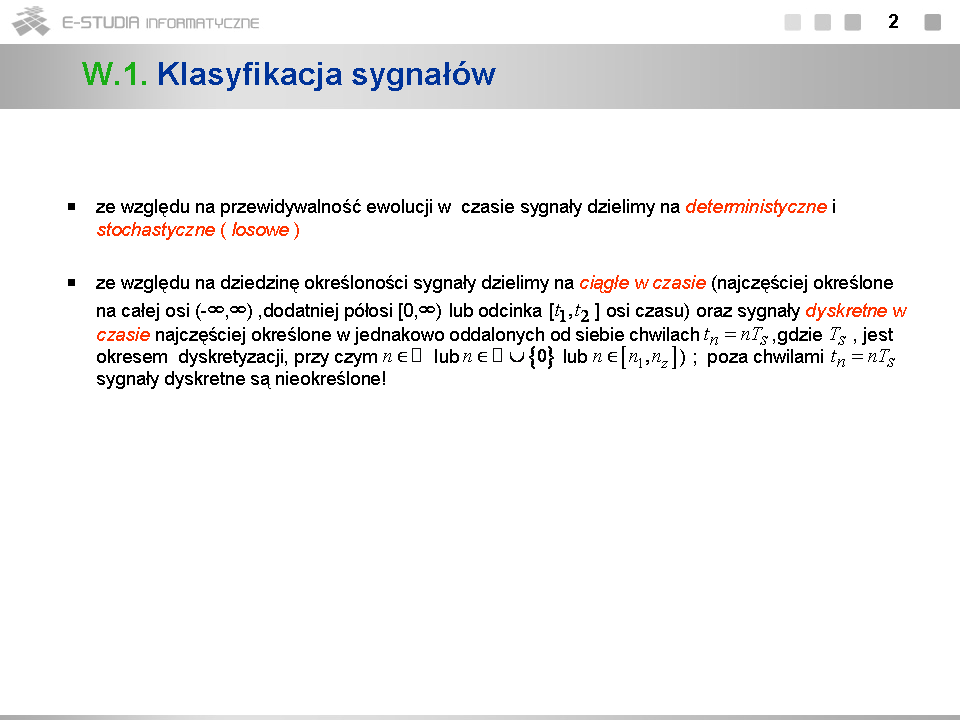
*Sygnałami harmonicznymi zespolonymi posługujemy się również w innych reprezentacjach sygnałów rzeczywistych, np. zbiór sygnałów | *Sygnałami harmonicznymi zespolonymi posługujemy się również w innych reprezentacjach sygnałów rzeczywistych, np. zbiór sygnałów <math>\left \{e^{jk\omega_0 t} : k\epsilon\Box\right \}\,</math> tworzy tzw. ''bazę'' rozwinięcia sygnału okresowego o okresie <math>T_0=2\pi/{\omega_0}</math> w zespolony szereg Fouriera (por. wzór (1.2)). | ||
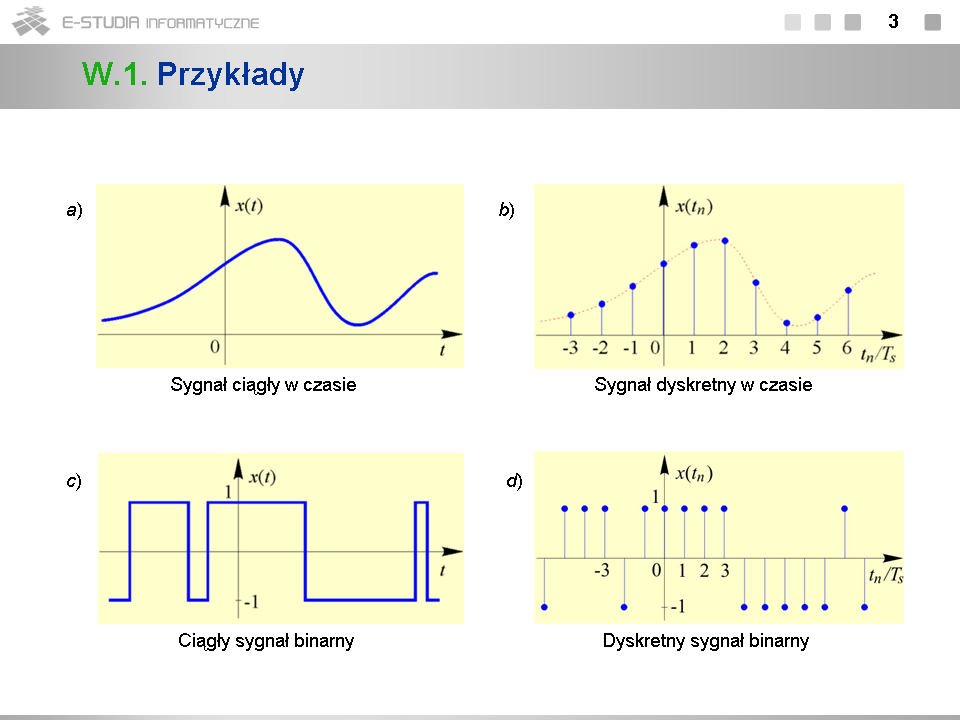
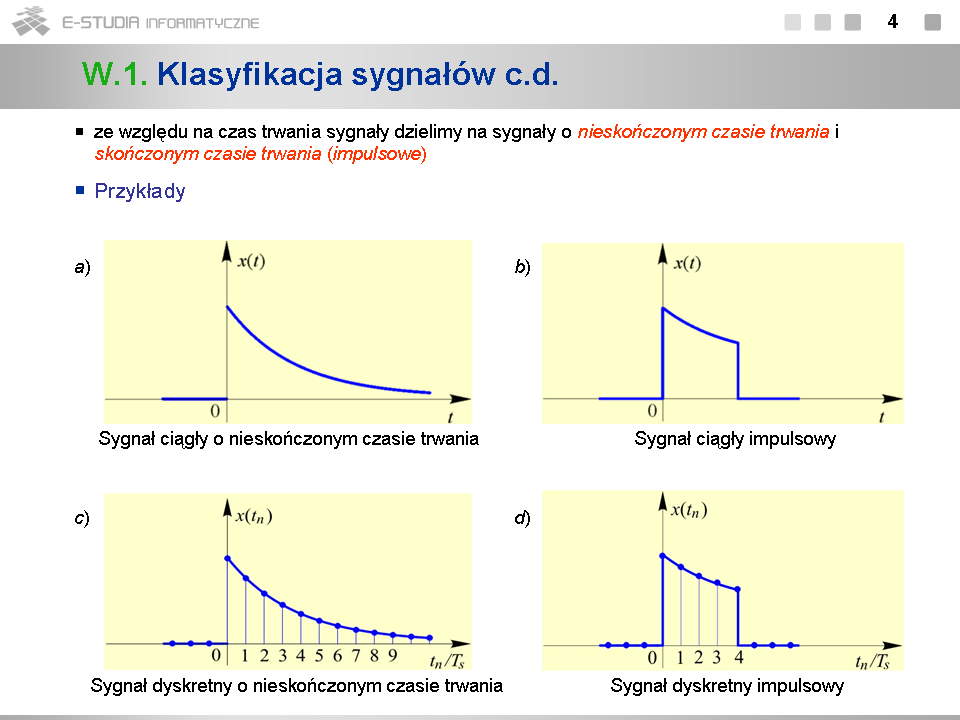
*Pojęcie ''sygnału analitycznego'', określonego wzorami (1.12) i (1.13), jest jednym z ważniejszych pojęć teorii sygnałów. Stanowi on uogólnienie na sygnały nieharmoniczne reprezentacji rzeczywistego sygnału harmonicznego <math>cos\omega_0 t\,</math> zespolonym sygnałem harmonicznym <math>e^{j\omega_0 t}=cos\omega_0 t+jsin\omega_0 t</math> . Zgodnie z definicją sygnał <math>e^{j\omega_0 t}\,</math> jest właśnie sygnałem analitycznym sygnału <math>\omega_0 t\,</math> . | |||