PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 34: | Linia 34: | ||
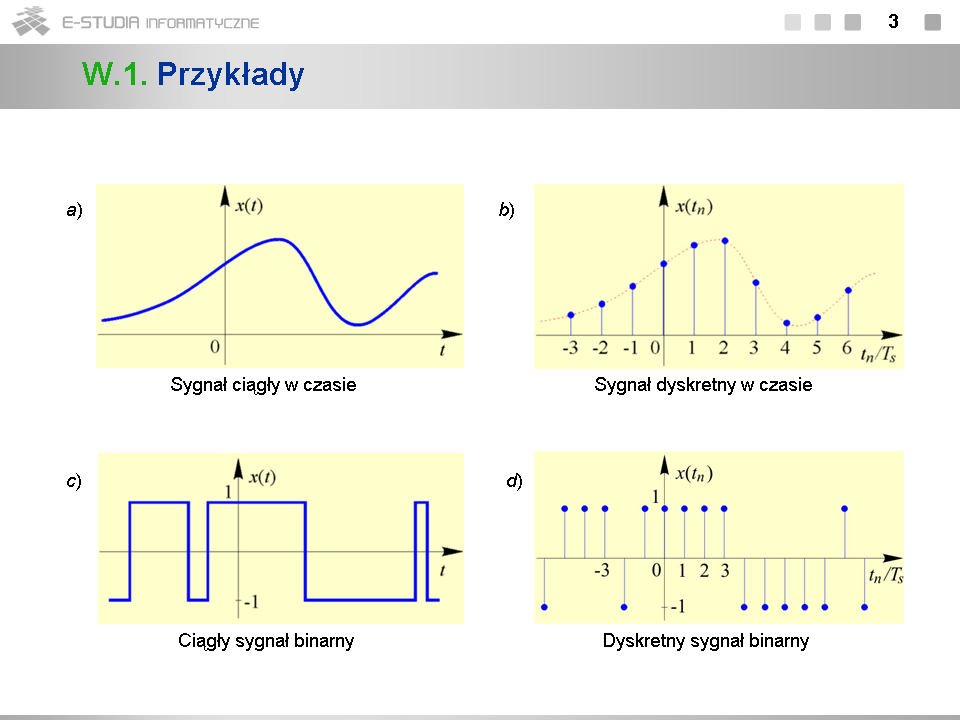
*Zwróćmy uwagę, że sygnały przedstawione na rys. b) i d) otrzymujemy w wyniku próbkowania sygnałów z rys. a) i odpowiednio c). Z sygnałami powstałymi w wyniku próbkowania sygnałów analogowych mamy w praktyce do czynienia najczęściej. Sygnałami dyskretnymi mogą być jednak także sygnały nie mające pierwowzorów analogowych, np. ciąg notowań dziennych kursu złotówki do dolara. Podkreślmy, że sygnał dyskretny jest w istocie rzeczy ciągiem liczb. | *Zwróćmy uwagę, że sygnały przedstawione na rys. b) i d) otrzymujemy w wyniku próbkowania sygnałów z rys. a) i odpowiednio c). Z sygnałami powstałymi w wyniku próbkowania sygnałów analogowych mamy w praktyce do czynienia najczęściej. Sygnałami dyskretnymi mogą być jednak także sygnały nie mające pierwowzorów analogowych, np. ciąg notowań dziennych kursu złotówki do dolara. Podkreślmy, że sygnał dyskretny jest w istocie rzeczy ciągiem liczb. | ||
*Sygnały analogowe będziemy oznaczać <math>x(t),\, y(t),\,...\,</math> ,zaś sygnały dyskretne - <math>x(t_n),\, y(t_n),\,...\,</math> ,lub w przypadku próbkowania równomiernego w chwilach <math>nT_s-x(nT_s),\, y(nT_s),\,...\,</math> , W odniesieniu do tych ostatnich z reguły operuje się czasem bezwymiarowym, unormowanym względem okresu próbkowania <math>T_s\,</math> . Oznacza się je wówczas symbolami <math>x[n],\,y[n],\,...\,</math> lub <math>x(n),\, y(n),\,...\,</math> , gdzie <math>n\epsilon\ | *Sygnały analogowe będziemy oznaczać <math>x(t),\, y(t),\,...\,</math> ,zaś sygnały dyskretne - <math>x(t_n),\, y(t_n),\,...\,</math> ,lub w przypadku próbkowania równomiernego w chwilach <math>nT_s-x(nT_s),\, y(nT_s),\,...\,</math> , W odniesieniu do tych ostatnich z reguły operuje się czasem bezwymiarowym, unormowanym względem okresu próbkowania <math>T_s\,</math> . Oznacza się je wówczas symbolami <math>x[n],\,y[n],\,...\,</math> lub <math>x(n),\, y(n),\,...\,</math> , gdzie <math>n\epsilon\Box\,</math> jest numerem próbki. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px"|[[Grafika:PS_M1_Slajd4.png]] | |||
|valign="top"| | |||
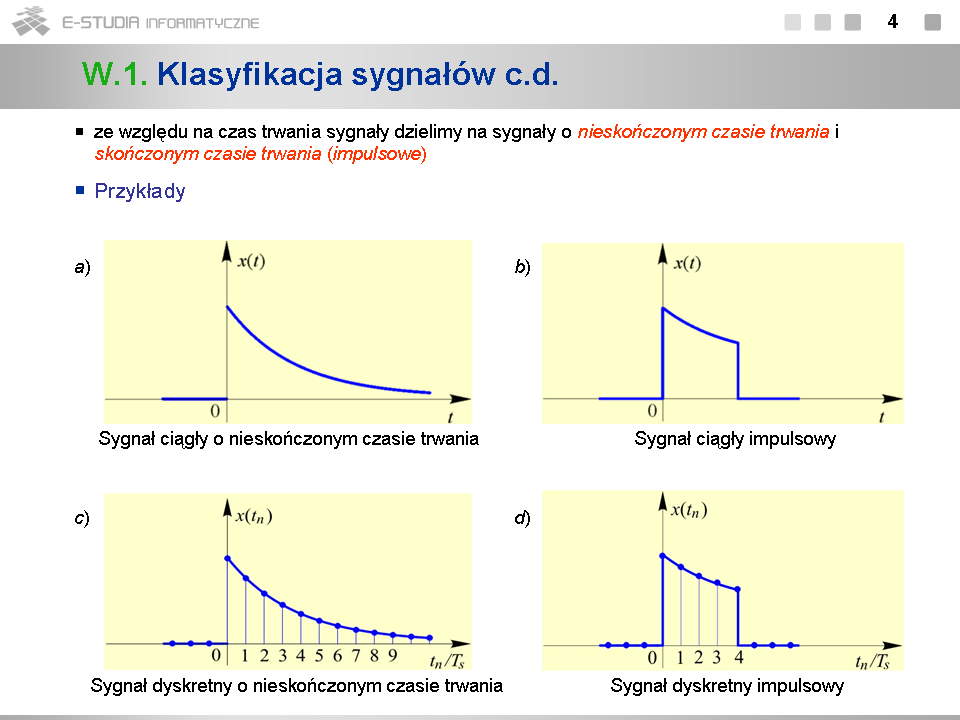
*Podobnie jak w poprzednich przykładach, sygnały z rys. c) i d) są spróbkowanymi sygnałami z rys. a) i b). | |||
*Terminem ''impuls'' określamy zazwyczaj sygnały o krótkim czasie trwania. Zwróćmy uwagę, że w myśl przyjętej definicji sygnał impulsowy niekoniecznie musi trwać w czasie krótko. Istotne jest jedynie, aby jego czas trwania był skończony. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px"|[[Grafika:PS_M1_Slajd5.png]] | |||
|valign="top"| | |||
* Reprezentację sygnału harmonicznego stanowi liczba zespolona <math>Ae^{j\varphi}\,</math> , nazywana ''amplitudą zespoloną'', gdzie <math>A\,</math> jest amplitudą sygnału, a <math>\varphi\,</math> – jego fazą. | |||
*W przypadku rozwinięcia sygnału okresowego o ustalonym okresie <math>T_0\,</math> w rzeczywisty trygonometryczny szereg Fouriera (1.1) jego reprezentacja jest zbiór liczb rzeczywistych <math>\left \{a_0, a_k, b_k : k\epsilon\Box \right \} \,</math> (zbiór ''współczynników Fouriera''), zaś w przypadku rozwinięcia w zespolony trygonometryczny szereg Fouriera (1.2) – zbiór liczb zespolonych <math>X_k : k\epsilon\Box\,</math> . | |||