CWGI Ćwiczenie 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 74: | Linia 74: | ||
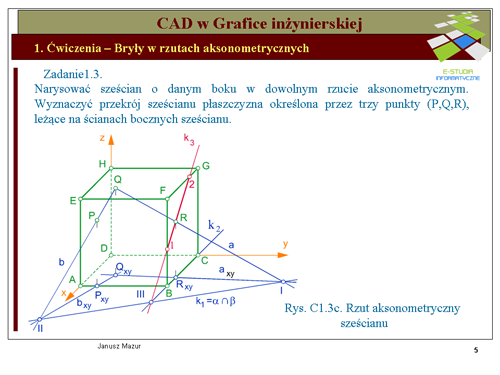
Krawędź <math>k_2\, </math> przecina krawędź <math>k_1\, </math> w punkcie oznaczonym cyfrą '''''III'''''. Punkt '''''III''''' jest, zatem punktem '''''wspólnym trójki płaszczyzn''''' <math>\alpha\,</math>, <math>\beta\,</math> i <math>\gamma\,</math>. Przez ten punkt, zgodnie z cytowanym wcześniej twierdzeniem, będzie przechodziła trzecia krawędź <math>k_3=\alpha \cap \gamma\, </math>. Drugi punkt wspólny tych płaszczyzn jest punktem '''''R''''' (z założenia punkt należący do płaszczyzny <math>\alpha\,</math> i <math>\beta\,</math>). Punkty '''''III''''' i '''''R''''' wyznaczą nam poszukiwaną krawędź <math>k_3\,</math>, która jest krawędzią przekroju płaszczyzny <math>\alpha\,</math> z jedną ze ścian sześcianu. Krawędź <math>k_3\,</math> przecina krawędzie sześcianu: '''''BF''''' w punkcie '''''1''''' oraz '''''CG''''' w punkcie '''''2'''''. Punkty te wyznaczają odcinek będący krawędzią przekroju ściany '''''BCGF''''' sześcianu płaszczyzną <math>\alpha\,</math>. | Krawędź <math>k_2\, </math> przecina krawędź <math>k_1\, </math> w punkcie oznaczonym cyfrą '''''III'''''. Punkt '''''III''''' jest, zatem punktem '''''wspólnym trójki płaszczyzn''''' <math>\alpha\,</math>, <math>\beta\,</math> i <math>\gamma\,</math>. Przez ten punkt, zgodnie z cytowanym wcześniej twierdzeniem, będzie przechodziła trzecia krawędź <math>k_3=\alpha \cap \gamma\, </math>. Drugi punkt wspólny tych płaszczyzn jest punktem '''''R''''' (z założenia punkt należący do płaszczyzny <math>\alpha\,</math> i <math>\beta\,</math>). Punkty '''''III''''' i '''''R''''' wyznaczą nam poszukiwaną krawędź <math>k_3\,</math>, która jest krawędzią przekroju płaszczyzny <math>\alpha\,</math> z jedną ze ścian sześcianu. Krawędź <math>k_3\,</math> przecina krawędzie sześcianu: '''''BF''''' w punkcie '''''1''''' oraz '''''CG''''' w punkcie '''''2'''''. Punkty te wyznaczają odcinek będący krawędzią przekroju ściany '''''BCGF''''' sześcianu płaszczyzną <math>\alpha\,</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_CW1_Slajd6.png]] | |||
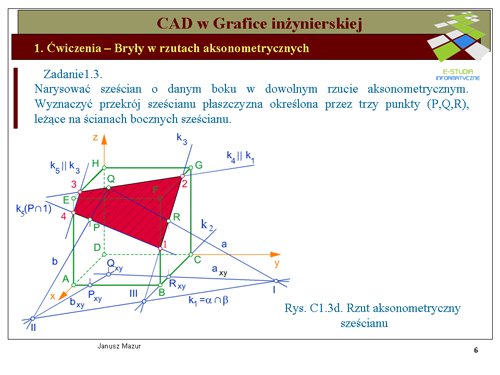
|valign="top"|Kolejne krawędzie przekroju sześcianu płaszczyzną <math>\alpha\,</math> można wyznaczyć powtarzając nasze rozumowanie, przy założeniu, że w miejsce jednej z płaszczyzn, np. <math>\gamma\,</math> wprowadzimy kolejną płaszczyznę przechodzącą przez inną ścianę sześcianu. Możemy jednak wyznaczyć następne boki przekroju korzystając z '''''niezmienników rzutowania równoległego''''' (rys.c1.3d). | |||
Wyznaczony wcześniej punkt '''''2''''' należy do krawędzi <math>k_3\,</math>, a wiec należy do płaszczyzny <math>\alpha\,</math>Punkt ten należy również do ściany '''''EFGH''''' sześcianu. Drugim punktem wspólnym płaszczyzny <math>\alpha\,</math> i górnej podstawy '''''EFGH''''' jest punkt '''''Q''''' z założenia należący do tych płaszczyzn. Zatem Kolejna krawędź <math>k_4\,</math> będzie przechodziła przez punkty '''''Q''''' i '''''2'''''. Krawędź <math>k_4\,</math>, jak wynika z niezmienników rzutowania równoległego (płaszczyzna kroi dwie równoległe do siebie płaszczyzny wzdłuż dwóch prostych równoległych) będzie równoległa do krawędzi <math>k_1\,</math>. | |||
Kolejna krawędź <math>k_5\,</math>, należąca do przekroju, będzie przechodziła przez punkt '''''3''''' znajdujący się na krawędzi <math>k_4\,</math> oraz boku '''''EH''''' sześcianu. Krawędź ta będzie również równoległa do krawędzi <math>k_3\,</math>. Zamykająca przekrój krawędź <math>k_6\,</math> będzie przechodziła przez punkty '''''4''''', '''''P''''', i '''''1'''''. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||