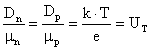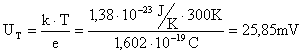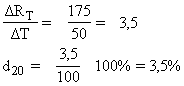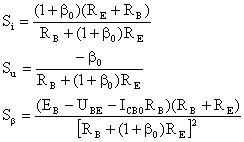PEE Zadania z rozwiązaniami: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 24 wersji utworzonych przez 3 użytkowników) | |||
| Linia 4: | Linia 4: | ||
[[Grafika:PEE_Zadania_rozw_1.jpg]] | [[Grafika:PEE_Zadania_rozw_1.jpg]] | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
Po likwidacji połączenia szeregowego rezystorów (<math>1\Omega\ | Po likwidacji połączenia szeregowego rezystorów (<math>1\Omega\ </math>, i <math>5\Omega\ </math>, oraz <math>2\Omega\ </math>, i <math>8\Omega\ </math>, ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się <math>R_{we} = 3,18\Omega</math>. | ||
| Linia 14: | Linia 15: | ||
'''Zadanie 2''' | '''Zadanie 2''' | ||
Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci <math>V_1\ | Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci <math>V_1\ </math>, i <math>V_2\ </math>,. Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: <math>i_1(t)=10\sqrt{2}\sin(\omega t)</math>, <math>i_2(t)=5\sqrt{2}\sin(\omega t-90^\circ)</math>, <math>e_1(t)=10\sin(\omega t+45^\circ)</math>, <math>e_2(t)=20\sqrt{2}\sin(\omega t+90^\circ)</math>, <math>R=2\Omega</math>, <math>X_L=\omega L=2\Omega</math>, <math>X_C=1/\omega C=1\Omega</math> | ||
[[Grafika:PEE_Zadania_rozw_2.jpg]] | [[Grafika:PEE_Zadania_rozw_2.jpg]] | ||
| Linia 55: | Linia 56: | ||
Prądy w obwodzie: | Prądy w obwodzie: | ||
: <math>I_{R1}=(V_1-E_1)/R=-9,5+j6,5</math> (prąd rezystora <math>R\ | : <math>I_{R1}=(V_1-E_1)/R=-9,5+j6,5</math> (prąd rezystora <math>R\ </math>, i źródła <math>e_1\ </math>,) | ||
: <math>I_{R2}=(V_1-V_2)/R=-0,5-j1,5</math> | : <math>I_{R2}=(V_1-V_2)/R=-0,5-j1,5</math> | ||
: <math>I_L=(V_2+E_2)/Z_L= 20,5+j6,5</math> | : <math>I_L=(V_2+E_2)/Z_L= 20,5+j6,5</math> | ||
| Linia 68: | Linia 69: | ||
[[Grafika:PEE_Zadania_rozw_3.gif]] | [[Grafika:PEE_Zadania_rozw_3.gif]] | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
A) Rozwiązanie obwodu dla składowej stałej (źródło <math>E\ | A) Rozwiązanie obwodu dla składowej stałej (źródło <math>E\ </math>,) | ||
Obwód dla składowej stałej przedstawiono na rysunku poniżej (a). Cewka w stanie ustalonym dla składowej stałej jest zwarciem a kondensator przerwą. | Obwód dla składowej stałej przedstawiono na rysunku poniżej (a). Cewka w stanie ustalonym dla składowej stałej jest zwarciem a kondensator przerwą. | ||
| Linia 83: | Linia 85: | ||
: <math>i_L^{(E)}=i_C^{(E)}=0</math> | : <math>i_L^{(E)}=i_C^{(E)}=0</math> | ||
B) Rozwiązanie obwodu dla składowej zmiennej (źródło <math>i(t)\ | B) Rozwiązanie obwodu dla składowej zmiennej (źródło <math>i(t)\ </math>,) | ||
Obwód dla składowej sinusoidalnej przedstawiono w postaci symbolicznej na (rys. b). Parametry symboliczne obwodu są następujące: <math>I=2e^{j90^\circ}</math>, <math>Z_L=j\omega L=j1</math>, <math>Z_C=1/j\omega C=-j2</math>. Impedancja zastępcza cewki i kondensatora jest równa | Obwód dla składowej sinusoidalnej przedstawiono w postaci symbolicznej na (rys. b). Parametry symboliczne obwodu są następujące: <math>I=2e^{j90^\circ}</math>, <math>Z_L=j\omega L=j1</math>, <math>Z_C=1/j\omega C=-j2</math>. Impedancja zastępcza cewki i kondensatora jest równa | ||
| Linia 116: | Linia 118: | ||
[[Grafika:PEE_Zadania_rozw_4.gif]] | [[Grafika:PEE_Zadania_rozw_4.gif]] | ||
Przyjąć następujące wartości parametrów elementów obwodu: <math>R=1\Omega</math>, <math>L_1=2H</math>, <math>L_2=1H</math>, <math>M=1H</math> oraz <math>i(t)=10\sin(t+45^\circ)A</math> | |||
''Rozwiązanie'' | |||
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono poniżej: | |||
[[Grafika:PEE_Zadania_rozw_4_a.gif]] | |||
Wielkości symboliczne charakteryzujące elementy obwodu: | |||
: <math>I={10 \over \sqrt{2}}e^{j45^\circ}</math> | |||
: <math>Z_1=j\omega(L_1-M)=j1</math> | |||
: <math>Z_2=j\omega(L_2-M)=0</math> | |||
: <math>Z_M=j\omega M=j1</math> | |||
Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | |||
: <math>Z={RZ_M \over R+Z_M}={1 \over \sqrt{2}}e^{j45^\circ}</math> | |||
Napięcie <math>U_{AB}</math> | |||
: <math>U_{AB}=ZI=j5</math> | |||
Prądy: | |||
: <math>I_R={U_{AB} \over R}=j5</math> | |||
: <math>I_1=0</math> | |||
: <math>I_2=I_3={U_{AB} \over Z_M}=5</math> | |||
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math>. Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | |||
: <math>U_{L_1}=j\omega L_1I_1+j\omega MI_2</math> | |||
: <math>U_{L_2}=j\omega L_2I_2+j\omega MI_1</math> | |||
<hr width="100%"> | |||
'''Zadanie 5''' | |||
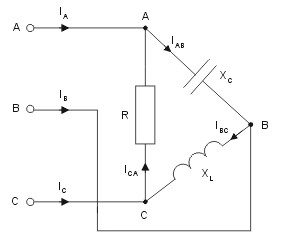
Wyznaczyć prądy w układzie trójfazowym o odbiorniku połączonym w trójkąt przedstawionym na rysunku poniżej. Sporządzić wykres wektorowy prądów i napięć. Przyjąć następujące wartości parametrów elementów: <math>|E_f|=200 V</math>, <math>R=X_L=X_C =10\Omega</math>. | |||
[[Grafika:PEE_Zadania_rozw_5.gif]] | |||
''Rozwiązanie'' | |||
Napięcia międzyfazowe: | |||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | |||
: <math>E_{AB}=200\sqrt{3}</math> | |||
: <math>E_{BC}=200\sqrt{3}e^{-j120^\circ}</math> | |||
: <math>E_{CA}=200\sqrt{3}e^{j120^\circ}</math> | |||
Prądy fazowe odbiornika: | |||
: <math>I_{AB}={E_{AB} \over -jX_C}=20\sqrt{3}e^{j90^\circ}</math> | |||
: <math>I_{BC}={E_{BC} \over jX_L}=20\sqrt{3}e^{-j210^\circ}</math> | |||
: <math>I_{CA}={E_{CA} \over R}=20\sqrt{3}e^{j120^\circ}</math> | |||
Prądy liniowe układu: | |||
: <math>I_A=I_{AB}-I_{CA}=17,32+j4,64</math> | |||
: <math>I_B=I_{BC}-I_{AB}=-30-j17,32</math> | |||
: <math>I_C=I_{CA}-I_{BC}=12,68+j12,68</math> | |||
Wykres wektorowy prądów i napięć przedstawiony jest poniżej: | |||
[[Grafika:PEE_Zadania_rozw_5_a.jpg]] | |||
<hr width="100%"> | |||
'''Zadanie 6''' | |||
Określić przebieg <math>u_C(t)</math> w stanie nieustalonym w obwodzie po przełączeniu. | |||
Dane: | |||
: <math>R_1=100\Omega</math> | |||
: <math>R_2=300\Omega</math> | |||
: <math>C=1000uF</math> | |||
: <math>e(t)=20V</math> | |||
[[Grafika:PEE_Zadania_rozw_6.jpg ]] | |||
''Rozwiązanie'' | |||
''1) Warunki początkowe w obwodzie (stan ustalony przed przełączeniem).'' | |||
Wobec <math>\omega=0</math> kondensator stanowi przerwę. Prąd płynie w obwodzie: <math>e-R_1-R_1</math>. Jego wartość: | |||
: <math>I={e \over 2R_1}={20 \over 200}=0,1</math> | |||
Napięcie na kondensatorze: | |||
: <math>U_{R1}=10</math> | |||
: <math>u_C(0^-)=10</math> | |||
''2) Stan ustalony w obwodzie po przełączeniu.'' | |||
Obwód podobny do tego z punktu 1 przy zastąpieniu <math>R_1\ </math>, przez <math>R_2\ </math>,. Prąd płynie w obwodzie: <math>e-R_1-R_2</math>. Jego wartość: | |||
: <math>I={e \over R_1+R_2}={20 \over 400}={1 \over 20}</math> | |||
Napięcie ustalone na kondensatorze: | |||
: <math>u_{C_u}(t)=IR_2=15</math> | |||
''3) Stan przejściowy (metoda klasyczna).'' | |||
Obwód dla stanu przejściowego pokazuje rysunek: | |||
[[Grafika:PEE_Zadania_rozw_6_a.jpg]] | |||
Z prawa prądowego Kirchhoffa: | |||
: <math>C{du_{C_p} \over dt}=-{u_{C_p} \over R_1}-{u_{C_p} \over R_2}</math> | |||
Po wstawieniu liczb otrzymuje się | |||
: <math>10^{-3}{du_{C_p} \over dt}=-u_{C_p}({1 \over 100}+{1 \over 300})</math> | |||
: <math>{du_{C_p} \over dt}=-u_{C_p}(10+3,33)=-13,33U_{C_p}</math> | |||
: <math>s=-13,33</math> | |||
: <math>u_{C_p}(t)=Ae^{-13,33t}</math> | |||
''4) Rozwiązanie pełne'' | |||
: <math>u_C(t)=u_{C_u}(t)+u_{C_p}(t)=15+Ae^{-13,33t}</math> | |||
Z warunku początkowego | |||
: <math>10=15+A \ \Rightarrow \ A=-5</math> | |||
Przebieg napięcia <math>u_C(t)</math> | |||
: <math>u_C(t)=15-5e^{-13,33}</math> | |||
<hr width="100%"> | |||
'''Zadanie 7''' | |||
Wyznaczyć przebiegi <math>u_C(t)</math> oraz <math>i_L(t)</math> w stanie nieustalonym w obwodzie po przełączeniu. | |||
Dane: | |||
: <math>i(t)=2\sqrt{2}\sin(t+90^\circ)</math> | |||
: <math>R = 1/2\Omega</math> | |||
: <math>L = 1 H</math> | |||
: <math>C = 1 F</math> | |||
[[Grafika:PEE_Zadania_rozw_7.gif]] | |||
''Rozwiązanie'' | |||
Warunki początkowe – stan ustalony w obwodzie przed przełączeniem | |||
[[Grafika:PEE_Zadania_rozw_7_a.jpg]] | |||
: <math>I=2e^{j90^\circ}</math> | |||
: <math>Z_L=j\omega L=j1</math> | |||
: <math>U_L=I{Z_LR \over Z_L + R}=2e^{j90^\circ}{j \cdot 0,5 \over j+0,5}=2e^{j90^\circ}{0,5e^{j90^\circ} \over 1,12e^{j63,4^\circ}}=0,89e^{j116,6^\circ}</math> | |||
: <math>I_L={U_L \over Z_L}=0,89e^{j26,6^\circ}</math> | |||
: <math>i_L(t)=0,89\sqrt{2}\sin(t+26,6^\circ)</math> | |||
: <math>i_L(0^-)=0,56 A</math> | |||
: <math>u_C(0^-)=0 V</math> | |||
Stan ustalony po przełączeniu | |||
[[Grafika:PEE_Zadania_rozw_7_b.jpg]] | |||
: <math>Z_C=-j{1 \over \omega C}=-j1</math> | |||
: <math>Z_{LC}={Z_CZ_L \over Z_C+Z_L}=\infty</math> | |||
: <math>U_{C_u}=IR=1e^{j90^\circ} \ \Rightarrow \ u_{C_u}(t)=\sqrt{2}\sin(t+90^\circ) \ \Rightarrow \ u_{C_u}(0^+)=\sqrt{2}</math> | |||
: <math>I_{L_u}={U_{C_u} \over Z_L}={1e^{j90^\circ} \over j1}=1 \ \Rightarrow \ i_{L_u}(t)=\sqrt{2}\sin(t) \ \Rightarrow \ i_{L_u}(0^+)=0</math> | |||
Stan przejściowy | |||
Warunki początkowe dla stanu przejściowego | |||
: <math>u_{C_p}(0^+)=u_C(0^-)-u_{C_u}(0^+)=0-1,41=-1,41 V</math> | |||
: <math>i_{L_p}(0^+)=i_L(0^-)-i_{L_u}(0^+)=0,56-0=0,56 A</math> | |||
Obwód w stanie przejściowym (schemat operatorowy) | |||
[[Grafika:PEE_Zadania_rozw_7_c.jpg]] | |||
Z metody potencjałów węzłowych | |||
: <math>U_{C_p}(s)={{-0,56 \over s}-1,41 \over 2+s+{1 \over s}}={-(1,41s+0,56) \over s^2+2s+1}={-1,41s-0,56 \over (s+1)^2}</math> | |||
: <math>u_{C_p}(t)=\lim_{s \to -1}{d \over ds} \left [ {-1,41s-0,56 \over (s+1)^2}e^{st}(s+1)^2 \right ]</math> | |||
: <math>u_{C_p}(t)=te^{st}(-1,41s-0,56)+e^{st}(-1,41)|_{s=-1}=0,85te^{-t}-1,41e^{-t}</math> | |||
Prąd kondensatora | |||
: <math>i_{c_p}(t)=C{du_{C_p} \over dt}=0,85[e^{-t}-te^{-t}]+1,41e^{-t}=2,26e^{-t}-0,85te^{-t}</math> | |||
Prąd rezystora | |||
: <math>i_{R_p}(t)={u_{C_p} \over R}=1,7te^{-t}-2,82e^{-t}</math> | |||
Prąd cewki | |||
: <math>i_{L_p}(t)=-i_{R_p}(t)-i_{C_p}(t)=0,56e^{-t}-0,85te^{-t}</math> | |||
Pełne rozwiązanie | |||
: <math>i_L(t)=i_{L_u}(t)+i_{L_p}(t)=\sqrt{2}\sin t+0,56e^{-t}-0,85te^{-t}</math> | |||
: <math>u_C(t)=u_{C_u}(t)+u_{C_p}(t)=\sqrt{2}\sin(t+90^\circ)+0,85te^{-t}-1,41e^{-t}</math> | |||
<hr width="100%"> | |||
'''Zadanie 8''' | |||
Wyznaczyć transmitancję napięciową układu przedstawionego na rysunku poniżej. Określić odpowiedź impulsową i skokową. | |||
Dane: | |||
: <math>R_1 = 5 \Omega</math> | |||
: <math>R_2 = 10 \Omega</math> | |||
: <math>C = 0,1 F</math> | |||
[[Grafika:PEE_Zadania_rozw_8.jpg]] | |||
''Rozwiązanie'' | |||
Impedancja zastępcza <math>R_2C</math>: | |||
: <math>Z_2(s)={R_2{1 \over sC} \over R_2+{1 \over sC}}={10{10 \over s} \over 10+{10 \over s}}={10 \over s+1}</math> | |||
Transmitancja napięciowa: | |||
: <math>T_v(s)={Z_2 \over R_1+Z_2}={{10 \over s+1} \over 5+{10 \over s+1}}={10 \over 5s+5+10}={10 \over 5s+15}={2 \over s+3}</math> | |||
Odpowiedź impulsowa: | |||
: <math>h(t)=L^{-1}[T_v(s)]=2e^{-3t}</math> | |||
Odpowiedź skokowa: | |||
: <math>y(t)=L^{-1}[{T_v(s) \over s}]=L^{-1}[{2 \over s(s+3)}]={2 \over 3}-{2 \over 3}e^{-3t}</math> | |||
<hr width="100%"> | |||
'''Zadanie 9''' | |||
Określić opis admitancyjny czwórnika. Na tej podstawie określić transmitancję napięciową obwodu. | |||
Dane: | |||
: <math>R_1 = 2 \Omega</math> | |||
: <math>R_2 = 5 \Omega</math> | |||
: <math>C = 0,5 F</math> | |||
: <math>L = 1 H</math> | |||
[[Grafika:PEE_Zadania_rozw_9.jpg]] | |||
''Rozwiązanie'' | |||
Z równań węzłowych obwodu względem punktu odniesienia mamy: | |||
: <math> | |||
\begin{bmatrix} | |||
{1 \over R_1}+{1 \over sL} & -{1 \over sL} \\ | |||
-{1 \over sL} & {1 \over R_2}+sC+{1 \over sL} | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
V_1 \\ | |||
V_2 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
I_1 \\ | |||
I_2 | |||
\end{bmatrix} | |||
</math> | |||
: <math> | |||
\begin{bmatrix} | |||
0,5+1/s & -1/s \\ | |||
-1/s & 0,2+0,5s+1/s} | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
V_1 \\ | |||
V_2 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
I_1 \\ | |||
I_2 | |||
\end{bmatrix} | |||
</math> | |||
Transmitancja napięciowa obliczana przy założeniu <math>I_2 = 0</math>: | |||
: <math>I_2=0=-{1 \over s} V_1+(0,2+0,5s+ 1/s)V_2</math> | |||
Stąd: | |||
: <math>{V_2 \over V_1}={1/s \over 0,2+0,5s + 1/s}</math> | |||
: <math>T_v(s)={V_2 \over V_1}={2 \over s^2+0,4s+2)}</math> | |||
<hr width="100%"> | |||
'''Zadanie 10''' | |||
Stała dyfuzji elektronów w temperaturze <math>27 ^oC</math> dla krzemu jest równa <math>D_n = 35·10^{-4} m^2 s^{-1}</math>. Obliczyć ruchliwość elektronów oraz stałą dyfuzji i ruchliwość dziur. | |||
''Rozwiązanie'' | |||
Zależność Einsteina wiąże ruchliwość ładunków ze stałą dyfuzji wzorem: | |||
[[Grafika:PEE_Zadania_rozw_10a.jpg]] | |||
W temperaturze 300 K napięcie UT jest równe | |||
[[Grafika:PEE_Zadania_rozw_10b.jpg]] | |||
Ruchliwość ładunku ujemnego jest zatem równa | |||
[[Grafika:PEE_Zadania_rozw_10c.jpg]] | |||
Ponieważ dla krzemu obowiązuje zależność | |||
[[Grafika:PEE_Zadania_rozw_10d.jpg]] | |||
to ruchliwość ładunku dodatniego można obliczyć ze wzoru | |||
[[Grafika:PEE_Zadania_rozw_10e.jpg]]. | |||
Wykonując podstawienie | |||
[[Grafika:PEE_Zadania_rozw_10f.jpg]] | |||
Stała dyfuzji dziur | |||
[[Grafika:PEE_Zadania_rozw_10g.jpg]] | |||
Po podstawieniu <math>D_p = 105·10^{-2} m^2 s^{-1}</math> | |||
<hr width="100%"> | |||
'''Zadanie 11''' | |||
Dla termistora, którego charakterystykę <math>R = f(T)</math> przedstawiono na rysunku wyznaczyć temperaturowy współczynnik rezystancji <math>d_{20}</math>. | |||
[[Grafika:PEE_Zadania_rozw_11.jpg]] | |||
''Rozwiązanie'' | |||
Temperaturowy współczynnik rezystancji termistora jest równy | |||
[[Grafika:PEE_Zadania_rozw_11a.jpg]] | |||
dla <math>R_T = R_{20} = 100 \Omega</math> | |||
[[Grafika:PEE_Zadania_rozw_11b.jpg]] | |||
Nachylenie stycznej do wykresu funkcji <math>RT = f(t)</math> w punkcie <math>Q(20, 100)</math> można oszacować | |||
z zależności: | |||
[[Grafika:PEE_Zadania_rozw_11c.jpg]] | |||
<hr width="100%"> | |||
'''Zadanie 12''' | |||
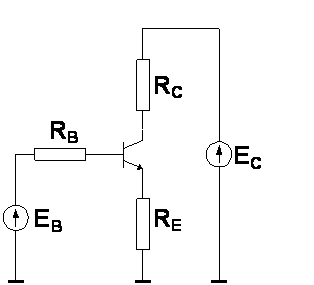
Wyznaczyć przyrost prądu kolektora w tranzystorze bipolarnym spowodowany przyrostem temperatury od <math>25 ^oC</math> do <math>100 ^oC</math> w układzie jak na rysunku. Dane: współczynnik wzmocnienia prądowego tranzystora w temperaturze <math>25 ^oC</math> <math>\beta_{25} = 330</math> oraz w temperaturze <math>100 ^oC</math> <math>\beta_{100} = 440</math>, prąd <math>I_{CB0(25)} = 200 pA</math>, <math>U_{CC} = 30 V</math>, <math>R_B = 430 k \Omega</math>, <math>R_E = 1 k\Omega</math>, <math>R_C</math> dowolne. | |||
[[Grafika:PEE_Zadania_rozw_12a.jpg]] | |||
''Rozwiązanie'' | |||
Przyrost wartości prądu kolektora można obliczyć stosując równanie stabilizacji punktu pracy | |||
[[Grafika:PEE_Zadania_rozw_12b.jpg]] | |||
Współczynniki stabilizacji dla układu jak na rysunku są równe | |||
[[Grafika:PEE_Zadania_rozw_12c.jpg]] | |||
Po podstawieniu danych | |||
<math>S_i = 187,5</math> | |||
<math>S_u = -0,434·10^{-3} S</math> | |||
<math>S_{\beta} = 0,022</math> | |||
Przyrost prądu <math>I_{CB0}</math> można wyznaczyć z zależności | |||
[[Grafika:PEE_Zadania_rozw_12d.jpg]] | |||
Przyrost napięcia baza-emiter oblicz się wiedząc, że współczynnik temperaturowy tego napięcia jest równy <math>-2,3 \frac{mV}{^oC}</math> | |||
[[Grafika:PEE_Zadania_rozw_12e.jpg]] | |||
Przyrost wartości współczynnika wzmocnienia prądowego <math>\beta_0</math> | |||
[[Grafika:PEE_Zadania_rozw_12f.jpg]] | |||
Podstawiając obliczone wartości do równania stabilizacji otrzymuje się | |||
[[Grafika:PEE_Zadania_rozw_12g.jpg]] | |||
Aktualna wersja na dzień 12:05, 5 wrz 2023
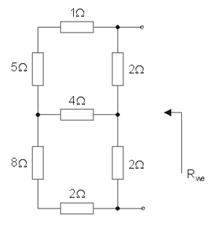
Zadanie 1
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej:
Rozwiązanie
Po likwidacji połączenia szeregowego rezystorów (, i , oraz , i , ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się .
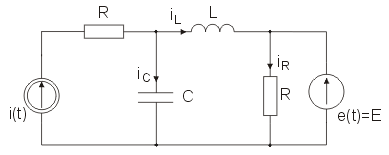
Zadanie 2
Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci , i ,. Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: , , , , , ,
Rozwiązanie
Wartości zespolone:
Równanie admitancyjne
Z rozwiązania tego macierzowego układu równań mamy
Prądy w obwodzie:
- (prąd rezystora , i źródła ,)
Zadanie 3
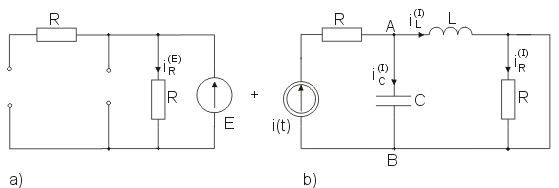
Wyznaczyć rozwiązanie obwodu z rysunku poniżej stosując zasadę superpozycji. Przyjąć , , , , , .
Rozwiązanie
A) Rozwiązanie obwodu dla składowej stałej (źródło ,)
Obwód dla składowej stałej przedstawiono na rysunku poniżej (a). Cewka w stanie ustalonym dla składowej stałej jest zwarciem a kondensator przerwą.
Dla prądu stałego tylko jeden prąd, , jest różny od zera. Jego wartość jest równa
B) Rozwiązanie obwodu dla składowej zmiennej (źródło ,)
Obwód dla składowej sinusoidalnej przedstawiono w postaci symbolicznej na (rys. b). Parametry symboliczne obwodu są następujące: , , . Impedancja zastępcza cewki i kondensatora jest równa
Napięcie i prądy w obwodzie:
Wartości prądów wyrażone w postaci czasowej:
Całkowite rozwiązanie obwodu jest sumą obu składowych:
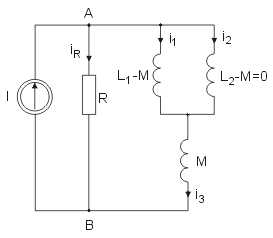
Zadanie 4
Wyznaczyć rozpływy prądów w obwodzie przedstawionym poniżej:
Przyjąć następujące wartości parametrów elementów obwodu: , , , oraz
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono poniżej:
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
Napięcie
Prądy:
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą . Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie
Zadanie 5
Wyznaczyć prądy w układzie trójfazowym o odbiorniku połączonym w trójkąt przedstawionym na rysunku poniżej. Sporządzić wykres wektorowy prądów i napięć. Przyjąć następujące wartości parametrów elementów: , .
Rozwiązanie
Napięcia międzyfazowe:
Prądy fazowe odbiornika:
Prądy liniowe układu:
Wykres wektorowy prądów i napięć przedstawiony jest poniżej:
Zadanie 6
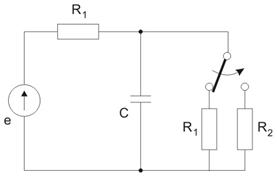
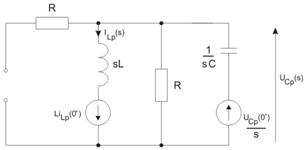
Określić przebieg w stanie nieustalonym w obwodzie po przełączeniu.
Dane:
Rozwiązanie
1) Warunki początkowe w obwodzie (stan ustalony przed przełączeniem).
Wobec kondensator stanowi przerwę. Prąd płynie w obwodzie: . Jego wartość:
Napięcie na kondensatorze:
2) Stan ustalony w obwodzie po przełączeniu.
Obwód podobny do tego z punktu 1 przy zastąpieniu , przez ,. Prąd płynie w obwodzie: . Jego wartość:
Napięcie ustalone na kondensatorze:
3) Stan przejściowy (metoda klasyczna).
Obwód dla stanu przejściowego pokazuje rysunek:
Z prawa prądowego Kirchhoffa:
Po wstawieniu liczb otrzymuje się
4) Rozwiązanie pełne
Z warunku początkowego
Przebieg napięcia
Zadanie 7
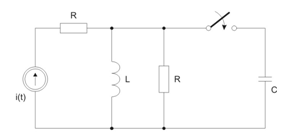
Wyznaczyć przebiegi oraz w stanie nieustalonym w obwodzie po przełączeniu.
Dane:
Rozwiązanie
Warunki początkowe – stan ustalony w obwodzie przed przełączeniem
Stan ustalony po przełączeniu
Stan przejściowy
Warunki początkowe dla stanu przejściowego
Obwód w stanie przejściowym (schemat operatorowy)
Z metody potencjałów węzłowych
Prąd kondensatora
Prąd rezystora
Prąd cewki
Pełne rozwiązanie
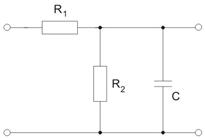
Zadanie 8
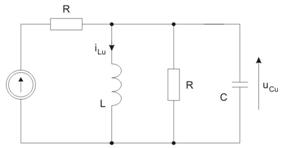
Wyznaczyć transmitancję napięciową układu przedstawionego na rysunku poniżej. Określić odpowiedź impulsową i skokową.
Dane:
Rozwiązanie
Impedancja zastępcza :
Transmitancja napięciowa:
Odpowiedź impulsowa:
Odpowiedź skokowa:
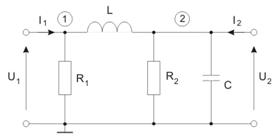
Zadanie 9
Określić opis admitancyjny czwórnika. Na tej podstawie określić transmitancję napięciową obwodu.
Dane:
Rozwiązanie
Z równań węzłowych obwodu względem punktu odniesienia mamy:
- Parser nie mógł rozpoznać (nieznana funkcja „\begin{bmatrix}”): {\displaystyle \begin{bmatrix} 0,5+1/s & -1/s \\ -1/s & 0,2+0,5s+1/s} \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} = \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} }
Transmitancja napięciowa obliczana przy założeniu :
Stąd:
Zadanie 10
Stała dyfuzji elektronów w temperaturze dla krzemu jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle D_n = 35·10^{-4} m^2 s^{-1}} . Obliczyć ruchliwość elektronów oraz stałą dyfuzji i ruchliwość dziur.
Rozwiązanie
Zależność Einsteina wiąże ruchliwość ładunków ze stałą dyfuzji wzorem:
W temperaturze 300 K napięcie UT jest równe
Ruchliwość ładunku ujemnego jest zatem równa
Ponieważ dla krzemu obowiązuje zależność
to ruchliwość ładunku dodatniego można obliczyć ze wzoru
Wykonując podstawienie
Stała dyfuzji dziur
Po podstawieniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle D_p = 105·10^{-2} m^2 s^{-1}}
Zadanie 11
Dla termistora, którego charakterystykę przedstawiono na rysunku wyznaczyć temperaturowy współczynnik rezystancji .
Rozwiązanie
Temperaturowy współczynnik rezystancji termistora jest równy
dla
Nachylenie stycznej do wykresu funkcji w punkcie można oszacować
z zależności:
Zadanie 12
Wyznaczyć przyrost prądu kolektora w tranzystorze bipolarnym spowodowany przyrostem temperatury od do w układzie jak na rysunku. Dane: współczynnik wzmocnienia prądowego tranzystora w temperaturze oraz w temperaturze , prąd , , , , dowolne.
Rozwiązanie
Przyrost wartości prądu kolektora można obliczyć stosując równanie stabilizacji punktu pracy
Współczynniki stabilizacji dla układu jak na rysunku są równe
Po podstawieniu danych
Parser nie mógł rozpoznać (błąd składni): {\displaystyle S_u = -0,434·10^{-3} S}
Przyrost prądu można wyznaczyć z zależności
Przyrost napięcia baza-emiter oblicz się wiedząc, że współczynnik temperaturowy tego napięcia jest równy
Przyrost wartości współczynnika wzmocnienia prądowego
Podstawiając obliczone wartości do równania stabilizacji otrzymuje się