Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
| (Nie pokazano 33 wersji utworzonych przez 2 użytkowników) | |||
| Linia 3: | Linia 3: | ||
<span id="cwiczenie_2_1">{{cwiczenie|2.1.|| | <span id="cwiczenie_2_1">{{cwiczenie|2.1.|| | ||
Dana jest funkcja afiniczna <math> | Dana jest funkcja afiniczna <math> f(x)=-x+2</math>. Wyznaczyć:<br> | ||
a) odwrotność tej funkcji,<br> | a) odwrotność tej funkcji,<br> | ||
b) funkcję odwrotną do <math> | b) funkcję odwrotną do <math>f</math>,<br> | ||
c) złożenie <math> | c) złożenie <math>f^2 = f \circ f</math>, <math>f^3 = f\circ f \circ f</math>, <math>f^4 = f\circ f | ||
\circ f\circ f</math>, <math> | \circ f\circ f</math>, <math>f^9 = f\circ f \circ f\circ f\circ f \circ | ||
f\circ f\circ f \circ f</math>.<br> | f\circ f\circ f \circ f</math>.<br> | ||
d) Czy istnieje malejąca funkcja | d) Czy istnieje malejąca funkcja | ||
afiniczna <math> | afiniczna <math>g</math> taka, że <math>(g\circ g )(x)=4x+3</math>? | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Co to jest odwrotność?<br> | a) Co to jest odwrotność?<br> | ||
b) Wystarczy wyznaczyć <math> | b) Wystarczy wyznaczyć <math>y</math> z równania <math>x=f(y)</math>.<br> | ||
c) Skorzystać z definicji złożenia. Składanie funkcji jest łączne.<br> | c) Skorzystać z definicji złożenia. Składanie funkcji jest łączne.<br> | ||
d) Niech <math> | d) Niech <math>g(x)=ax +b</math>. Jakie warunki muszą spełniać współczynniki <math>a</math> | ||
i <math> | i <math>b</math>, aby <math>(g\circ g )(x)=4x+3</math>? | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Odwrotnością | a) Odwrotnością | ||
funkcji <math> | funkcji <math>f</math> jest funkcja | ||
<math> | <math>x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2}</math>.<br> | ||
b) Wyznaczamy <math> | b) Wyznaczamy <math>y</math> z równania <math>x=-y+2</math>. Stąd <math>g(x)=-x+2</math> jest | ||
funkcją odwrotną do <math> | funkcją odwrotną do <math>f</math>. A więc funkcją odwrotną do <math>f</math> jest | ||
<math> | <math>f</math>.<br> | ||
c) Funkcją odwrotną do <math> | c) Funkcją odwrotną do <math>f</math> jest <math>f</math>, więc <math>f\circ f =\mathrm{id} \,</math>, gdzie | ||
<math> | <math>\mathrm{id}\,: x\mapsto x</math> oznacza odwzorowanie identycznościowe. Wobec | ||
tego <math> | tego <math>f^3 =(f\circ f)\circ f=\mathrm{id}\,\circ f=f</math>. Podobnie <math>f^4=(f\circ | ||
f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}\,</math>. Spostrzegamy, że: | f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id} \,</math>. Spostrzegamy, że: | ||
<center><math> | <center><math> | ||
f^n | |||
\left\{\begin{array}{ll} f, &\ | = | ||
nieparzystą},\\ | \left \{ \begin{array}{ll} f, & \text{ jeśli } n \text{ jest liczbą nieparzystą},\\ | ||
\mathrm{id} | \mathrm{id}, & \text{ jeśli } n \text{ jest liczbą parzystą},\end{array} \right . </math></center> | ||
parzystą},\end{array}\right . | |||
</math></center> | |||
wobec tego <math> | wobec tego <math>f^9=f</math>.<br> | ||
d) Jeśli <math> | d) Jeśli <math>g(x)=ax+b</math>, to <math>(g\circ g)(x)=a(ax+b)+b=a^2 x+ab+b</math>. | ||
Jeśli <math> | Jeśli <math>(g\circ g)(x)=4x+3</math>, to współczynniki <math>a</math>, <math>b</math> muszą | ||
spełniać układ równań: | spełniać układ równań: | ||
<center><math> | <center><math> \left \{ \begin{array}{l} a^2 = 4\\ (a+1)b = 3 \end{array} \right . </math></center> | ||
(a+1)b=3 | |||
</math></center> | |||
który | który | ||
spełniają dwie pary liczb <math> | spełniają dwie pary liczb <math>(a,b)\in\{(-2, -3), \ (2, 1)\}</math>. | ||
Funkcja <math> | Funkcja <math>g_1 (x)=-2x-3</math> jest malejąca, a <math>g_2 (x)=2x+1</math> jest | ||
rosnącą funkcją afiniczną. | rosnącą funkcją afiniczną. | ||
</div></div> | </div></div> | ||
| Linia 59: | Linia 55: | ||
Dana jest homografia | Dana jest homografia | ||
<math> | <math> f(x) = \frac{x+1}{x-1}</math>. Wyznaczyć:<br> | ||
a) odwrotność tej homografii,<br> | a) odwrotność tej homografii,<br> | ||
b) homografię odwrotną,<br> | b) homografię odwrotną,<br> | ||
c) złożenie <math> | c) złożenie <math>f^2 = f \circ f</math>, <math>f^3 = f\circ | ||
f \circ f</math>, <math> | f \circ f</math>, <math>f^4 = f\circ f \circ f\circ f</math> oraz <math>f^{11} = f\circ | ||
f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | ||
f </math>.<br> | f</math>.<br> | ||
d) Czy istnieje homografia <math> | d) Czy istnieje homografia <math>g: \mathbb{R} \mapsto \mathbb{R}</math> taka, że | ||
<math> | <math>g \circ g = f</math>? | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a), b) c) Zastosować wskazówki do [[#cwiczenie_2_1|ćwiczenia 2.1.]]<br> | a), b) c) Zastosować wskazówki do [[#cwiczenie_2_1|ćwiczenia 2.1.]]<br> | ||
d) Niech <math> | d) Niech <math>g(x)=\frac{ax +b}{cx +d}</math>. | ||
Zauważyć, że można przyjąć, że <math> | Zauważyć, że można przyjąć, że <math>c=1</math> (dlaczego?). Jakie równania | ||
muszą spełniać współczynniki <math> \ | muszą spełniać współczynniki <math>\ a,\ b,\ d</math>, aby <math>g\circ g=f</math>? | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Odwrotnością danej homografii jest | a) Odwrotnością danej homografii jest | ||
<math> | <math>x\mapsto\frac{1}{f(x)}=\frac{x-1}{x+1}</math>.<br> | ||
b) Homografię odwrotną do <math> | b) Homografię odwrotną do <math>f</math> otrzymamy, wyznaczając <math>x</math> z | ||
równania <math> | równania <math>y=\frac{x+1}{x-1}</math>. Stąd | ||
<math> | <math>x=\frac{y+1}{y-1}</math>, czyli | ||
homografią odwrotną do <math> | homografią odwrotną do <math>f</math> jest ta sama funkcja.<br> | ||
c) Skoro <math> | c) Skoro <math>f^{-1}=f</math>, więc - podobnie jak w [[#cwiczenie_2_1|ćwiczeniu 2.1.]] - złożenie | ||
<math> | <math>f\circ f=\mathrm{id}</math>, <math>f^4=(f\circ f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}</math>. | ||
Spostrzegamy, że: | Spostrzegamy, że: | ||
<center><math> | <center><math> | ||
f^n = | |||
\left\{\begin{array}{ll} f, &\ | \left \{ | ||
nieparzystą},\\ | \begin{array}{ll} f, & \text{jeśli } n \text{ jest liczbą nieparzystą}, \\ | ||
\mathrm{id} | \mathrm{id}, & \text{jeśli } n \text{ jest liczbą parzystą}, | ||
parzystą, | \end{array} | ||
\right . | |||
</math></center> | </math></center> | ||
wobec tego <math> | wobec tego <math>f^3=f</math>, <math>f^{11}=f</math>.<br> | ||
d) Niech <math> | d) Niech <math>g(x)=\frac{ax+b}{cx+d}</math>. Współczynnik <math>c\neq 0</math>, gdyż | ||
w przeciwnym przypadku funkcja <math> | w przeciwnym przypadku funkcja <math>g</math> byłaby afiniczna i złożenie | ||
<math> | <math>g\circ g</math> byłoby funkcją afiniczną, co nie jest możliwe. Skoro <math>c\neq 0</math> | ||
możemy podzielić licznik i mianownik rozważanego ułamka przez stałą <math> | możemy podzielić licznik i mianownik rozważanego ułamka przez stałą <math>c</math> | ||
i przyjąć, że <math> | i przyjąć, że <math>c=1</math> to znaczy: <math>g(x)=\frac{ax+b}{x+d}</math>. Wobec tego | ||
<center><math> \ | <center><math>\begin{align} (g\circ g)(x)=&g(g(x)) | ||
=\frac{ag(x)+b}{g(x)+d}\\=&\frac{a\frac{ax+b}{x+d}+b}{\frac{ax+b}{x+d}+d} | =\frac{ag(x)+b}{g(x)+d}\\=&\frac{a\frac{ax+b}{x+d}+b}{\frac{ax+b}{x+d}+d} | ||
=\frac{a(ax+b)+b(x+d)}{ax+b+d(x+d)}=\frac{(a^2+b)x+(ab+bd)}{(a+d)x+(b+d^2)}.\ | =\frac{a(ax+b)+b(x+d)}{ax+b+d(x+d)}=\frac{(a^2+b)x+(ab+bd)}{(a+d)x+(b+d^2)}.\end{align} | ||
</math></center> | </math></center> | ||
Równość <math> | Równość <math>g\circ g=f</math> zachodziłaby, gdyby odpowiednie współczynniki homografii <math>g\circ g</math> oraz <math>f</math> były równe, | ||
<center><math> | <center><math>0\neq a^2+b=b(a+d)=a+d=-(b+d^2)</math>.</center> | ||
Ale jest to niemożliwe, gdyż z równości <math> | Ale jest to niemożliwe, gdyż z równości <math>b(a+d)=a+d</math> wynika, że <math>b=1</math>, co pociąga za sobą w konsekwencji nierówność: <math>1\leq a^2 +1=a^2 | ||
+b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math> | +b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math>g:\mathbb{R}\mapsto\mathbb{R}</math>, aby <math>g\circ g=f</math>. | ||
</div></div> | </div></div> | ||
| Linia 118: | Linia 115: | ||
Wyrazić w prostszej postaci:<br> | Wyrazić w prostszej postaci:<br> | ||
a) <math> | a) <math>\arcsin(\cos x)</math>, <math>\arccos(\sin x)</math>,<br> | ||
b) <math> | b) <math>\sin(\arccos x)</math>, <math>\cos(\arcsin x)</math>,<br> | ||
c) <math> | c) <math>\mathrm{arctg}\,(\mathrm{ctg}\, x)</math>, <math>\mathrm{arc\,ctg}\,(\mathrm{tg}\, x )</math>,<br> | ||
d) <math> | d) <math>\mathrm{tg}\, (\mathrm{arc\,ctg}\, x )</math>, <math>\mathrm{ctg}\, (\mathrm{arctg}\, x )</math>,<br> | ||
e) <math> | e) <math>\sinh({\rm arcosh\, } x)</math>, <math>\cosh({\rm arsinh\, } x)</math>. | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Skorzystać ze | a) Skorzystać ze | ||
związku: <math> | związku: <math>\arccos x=\arcsin(-x)+\frac{\pi}{2}</math>.<br> | ||
b) Skorzystać z jedynki trygonometrycznej. | b) Skorzystać z jedynki trygonometrycznej. | ||
</div></div> | </div></div> | ||
| Linia 133: | Linia 130: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Zauważmy, że | a) Zauważmy, że | ||
funkcja <math> | funkcja <math>x\mapsto\arcsin(\cos x)</math> jest określona w każdym punkcie | ||
zbioru liczb rzeczywistych i jest okresowa o okresie <math> | zbioru liczb rzeczywistych i jest okresowa o okresie <math>2\pi</math>. | ||
Wystarczy więc wyznaczyć jej wartości w jakimkolwiek przedziale | Wystarczy więc wyznaczyć jej wartości w jakimkolwiek przedziale | ||
postaci <math> | postaci <math>[a-\pi, a+\pi]</math>. Funkcja cosinus jest parzysta, stąd złożenie | ||
<math> | <math>x\mapsto\arcsin(\cos x)</math> jest funkcją parzystą. Wystarczy więc | ||
rozważyć wyrażenie <math> | rozważyć wyrażenie <math>\arcsin(\cos x)</math> w zbiorze <math>0\leq x\leq \pi</math>. | ||
Jeśli <math> | Jeśli <math>0\leq x\leq \pi</math>, to różnica | ||
<math> | <math>\frac{\pi}{2}-x\in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]</math>. Korzystając ze wzoru | ||
redukcyjnego: <math> | redukcyjnego: <math>\cos x=\sin\left(\frac{\pi}{2}-x\right)</math>, otrzymujemy | ||
<center><math> | <center><math>\arcsin(\cos | ||
x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x | x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x</math>,</center> | ||
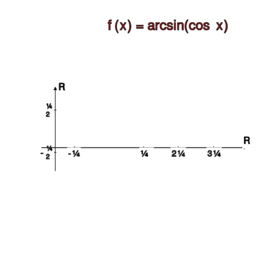
dla <math> | dla <math>0\leq x\leq \pi</math>. Wobec parzystości rozważanej funkcji mamy dla <math>-\pi\leq x\leq\pi</math> równość <center><math>\arcsin(\cos x)=\frac{\pi}{2}-|x|</math>.</center> <br> | ||
[[File:an1c02.0020.svg|375x270px|thumb|right|Rysunek do ćwiczenia 2.3.(a)]] | |||
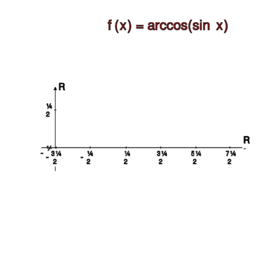
[[File:an1c02.0030.svg|375x270px|thumb|right|Rysunek do ćwiczenia 2.3.(a)]] | |||
Funkcja <math> | Funkcja <math>x\mapsto \arccos(\sin x)</math> ma okres <math>2\pi</math> i jest określona dla wszystkich liczb rzeczywistych. Podobnie jak w poprzednim przykładzie określimy więc jej wartość w przedziale <math>[-\pi, \pi]</math>. Dzięki okresowości wystarczy to, aby określić jej wartość dla dowolnej liczby rzeczywistej <math>x</math>. Zauważmy, że funkcja <math>y\mapsto f(y)=\arccos y-\frac{\pi}{2}</math> jest nieparzysta, więc <math>f(-y)=-f(y)</math>, stąd | ||
<center> | <center> | ||
<math> | <math>\arccos (-y)=\pi -\arccos y</math> dla <math> | ||
|y|\leq\frac{\pi}{2} | |y|\leq\frac{\pi}{2}</math> | ||
</math> | |||
</center> | </center> | ||
Rozumując jak poprzednio, na mocy wzoru | Rozumując jak poprzednio, na mocy wzoru | ||
redukcyjnego równość: | redukcyjnego równość: | ||
<math> | <math>\sin x=\cos \bigg(\frac{\pi}{2}-x\bigg)</math>. Stąd | ||
<center> | <center> | ||
<math> | <math>\arccos (\sin x)) =\arccos\bigg(\cos\bigg(\frac{\pi}{2}-x\bigg)\bigg) =\frac{\pi}{2}-x</math>, | ||
</math> | |||
</center> | </center> | ||
dla <math> | dla <math>x\in \bigg[0, \frac{\pi}{2}\bigg]</math>. Natomiast dla | ||
<math> | <math>x\in \bigg[\frac{\pi}{2},\pi\bigg]</math> mamy równość | ||
<center> | <center> | ||
<math> | <math>\arccos (\sin x) =-\bigg(\frac{\pi}{2}-x\bigg) =x-\frac{\pi}{2}</math> | ||
-\bigg(\frac{\pi}{2}-x\bigg) | |||
x-\frac{\pi}{2} | |||
</math> | |||
</center> | </center> | ||
Stąd dla | Stąd dla | ||
<math> | <math>\bigg|x-\frac{\pi}{2}\bigg|\leq \frac{\pi}{2}</math> mamy | ||
<center> | <center> | ||
<math> | <math>\arccos (\sin x)) =\bigg|x-\frac{\pi}{2}\bigg|</math> | ||
\bigg|x-\frac{\pi}{2}\bigg| | |||
</math> | |||
</center> | </center> | ||
Korzystając teraz z nieparzystości | Korzystając teraz z nieparzystości | ||
funkcji | funkcji | ||
<math> | <math>y\mapsto \arccos y-\frac{\pi}{2}</math> dla <math>x\in [-\pi, 0]</math>, | ||
otrzymamy <math> | otrzymamy <math>\arccos(\sin x)=\pi-\bigg|x+\frac{\pi}{2}\bigg|</math>. Stąd | ||
ostatecznie dla <math> | ostatecznie dla <math>x\in[-\pi, \pi]</math> mamy | ||
<center> | <center> | ||
<math> | <math> \arccos ( \sin x)= \left \{ | ||
}& -\pi \leq x\leq-\frac{\pi}{2}\\ &\frac{\pi}{2}-x, &\ | \begin{align} | ||
}& -\frac{\pi}{2} \leq x\leq \frac{\pi}{2}\\ &x-\frac{\pi}{2}, | & \frac{3\pi}{2}+x, & \text{ dla } & -\pi \leq x \leq - \frac{\pi}{2} \\ | ||
&\ | & \frac{\pi}{2} - x, & \text{ dla } & - \frac{\pi}{2} \leq x \leq \frac{\pi}{2} \\ | ||
\right. | & x -\frac{\pi}{2}, & \text{ dla } & + \frac{\pi}{2} \leq x \leq \pi. | ||
</math> | \end{align} | ||
\right . </math> | |||
</center> | </center> | ||
b) Niech <math> | b) Niech <math>y=\arccos x</math>. Zatem <math>\sin y\geq 0</math>. Z jedynki trygonometrycznej: <math>\sin^2 y=1-\cos^2 y=1-x^2</math>. Stąd <math>\sin(\arccos x)=\sqrt{1-x^2}</math> dla <math>-1\leq x\leq 1</math>. | ||
Podobnie dostajemy równość: <math> | Podobnie dostajemy równość: <math>\cos(\arcsin x)=\sqrt{1-x^2}</math> dla <math>-1\leq x\leq 1</math>.<br> | ||
c) Funkcja <math> | c) Funkcja <math>x\mapsto \mathrm{arctg}\,(\mathrm{ctg}\, x)</math> jest nieparzysta, gdyż jest złożeniem dwóch funkcji nieparzystych: <math>x\mapsto \mathrm{ctg}\, x</math> oraz <math>u\mapsto \mathrm{arctg}\, u</math>. Jest okresowa o okresie <math>\pi</math> wystarczy więc rozważyć ją np. na przedziale <math>0<x<\pi</math>. Ze wzoru redukcyjnego mamy <math>\mathrm{ctg}\, x=\mathrm{tg}\,\left(\frac{\pi}{2}-x\right)</math>, stąd | ||
<center> | <center> | ||
<math> | <math>\mathrm{arctg}\,(\mathrm{ctg}\, x) =\mathrm{arctg}\,\left(\mathrm{tg}\,\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x</math>, | ||
\mathrm{arctg}\,\left(\mathrm{tg}\,\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x | |||
</math> | |||
</center> | </center> | ||
dla <math> | dla <math>0<x<\pi</math>. | ||
Podobnie <math> | Podobnie <math>x\mapsto \mathrm{arc\,ctg}\,(\mathrm{tg}\, x)</math> jest nieparzysta, okresowa o okresie <math>\pi</math>. Wystarczy więc rozważyć ją np. w przedziale <math>\bigg(-\frac{\pi}{2},\frac{\pi}{2}\bigg)</math>, gdzie zachodzi równość: | ||
<center><math> | <center><math>\mathrm{arc\,ctg}\,(\mathrm{tg}\, x)=\mathrm{arc\,ctg}\,(\mathrm{ctg}\,(\frac{\pi}{2}-x))=\frac{\pi}{2}-x</math></center> | ||
</math></center> | |||
d) Pamiętając, że <math> | d) Pamiętając, że <math>\mathrm{tg}\, u=\frac{1}{\mathrm{ctg}\, u}</math>, otrzymamy | ||
<math> | <math>\mathrm{tg}\,(\mathrm{arc\,ctg}\, x)=\frac{1}{\mathrm{ctg}\,(\mathrm{arc\,ctg}\, x)}=\frac{1}{x}</math>, dla <math>x\neq 0</math>. | ||
Podobnie: <math> | Podobnie: <math>\mathrm{ctg}\,(\mathrm{arctg}\, x)=\frac{1}{\mathrm{tg}\,(\mathrm{arctg}\, x)}=\frac{1}{x}</math>, dla <math>x\neq 0</math>.<br> | ||
e) Z jedynki hiperbolicznej <math> | e) Z jedynki hiperbolicznej <math>\sinh(u)=\sqrt{\cosh^2 u -1}</math> dla <math>u\geq 0</math>. Po podstawieniu <math>u:={\rm arcosh\, } x</math>, dostajemy <math>\sinh({\rm arcosh\, } x)=\sqrt{x^2-1}</math>, dla <math>x\geq 1</math>. | ||
Z kolei <math> | Z kolei <math>\cosh^2 v=1+\sinh^2v</math>. Funkcja <math>x\mapsto \cosh({\rm arsinh\, } x)</math> jest określona na całym zbiorze liczb rzeczywistych i jest parzysta. Mamy równość: | ||
<center><math> | <center><math>\cosh({\rm arsinh\, } x) =\sqrt{1+\sinh^2({\rm arsinh\, } x)} =\sqrt{1+x^2}</math>,</center> | ||
\sqrt{1+\sinh^2({\rm arsinh\, } x)} | |||
\sqrt{1+x^2} | |||
</math></center> | |||
prawdziwą dla wszystkich liczb rzeczywistych <math> | prawdziwą dla wszystkich liczb rzeczywistych <math>x</math>. | ||
</div></div> | </div></div> | ||
<span id="cwiczenie_2_4">{{cwiczenie|2.4.|| | <span id="cwiczenie_2_4">{{cwiczenie|2.4.|| | ||
Wykazać, że dla dowolnych liczb <math> | Wykazać, że dla dowolnych liczb <math>x</math>, <math>y</math> | ||
zachodzą równości:<br> | zachodzą równości:<br> | ||
a) <math> | a) <math>\cosh(x+y)=\cosh x \cosh y+\sinh x\sinh y</math>,<br> | ||
b) <math> | b) <math>\sinh(x+y)=\sinh x\cosh y+\cosh x \sinh y</math>. | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Warto przekształcić wpierw prawą | a) Warto przekształcić wpierw prawą | ||
stronę równości, skorzystać z definicji funkcji <math> | stronę równości, skorzystać z definicji funkcji <math>\sinh</math> oraz | ||
<math> | <math>\cosh</math>, wykonać mnożenie i zredukować wyrazy podobne.<br> | ||
b) Należy postąpić podobnie jak w punkcie a) zadania. | b) Należy postąpić podobnie jak w punkcie a) zadania. | ||
</div></div> | </div></div> | ||
| Linia 264: | Linia 237: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Z definicji funkcji | a) Z definicji funkcji | ||
<math> | <math>\sinh</math> i <math>\cosh</math> mamy: | ||
<center><math> \ | <center><math>\begin{align} 4(\cosh x \cosh y+\sinh x\sinh y)&=(e^x+e^{-x} | ||
)(e^y+e^{-y} | )(e^y+e^{-y} | ||
)(e^x-e^{-x} )(e^y-e^{-y} )\\ | )(e^x-e^{-x} )(e^y-e^{-y} )\\ | ||
| Linia 272: | Linia 245: | ||
&=2(e^{x+y}+e^{-(x+y)})\\ | &=2(e^{x+y}+e^{-(x+y)})\\ | ||
&=4\cosh(x+y), | &=4\cosh(x+y), | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
stąd <math> | stąd <math>\cosh x \cosh y+\sinh x\sinh y=\cosh(x+y)</math>. | ||
b) Dokonując podobnych przekształceń jak w punkcie a), otrzymujemy: | b) Dokonując podobnych przekształceń jak w punkcie a), otrzymujemy: | ||
<center><math> \ | <center><math>\begin{align} 4(\sinh x \cosh y+\cosh x\sinh y)&=(e^x-e^{-x} | ||
)(e^y+e^{-y} | )(e^y+e^{-y} | ||
)(e^x+e^{-x} )(e^y-e^{-y} )\\ | )(e^x+e^{-x} )(e^y-e^{-y} )\\ | ||
| Linia 285: | Linia 258: | ||
&=2(e^{x+y}-e^{-(x+y)})\\ | &=2(e^{x+y}-e^{-(x+y)})\\ | ||
&=4\sinh(x+y), | &=4\sinh(x+y), | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
stąd <math> | stąd <math>\sinh x \cosh y+\cosh x\sinh y=\sinh(x+y)</math>. | ||
</div></div> | </div></div> | ||
<span id="cwiczenie_2_5">{{cwiczenie|2.5.|| | <span id="cwiczenie_2_5">{{cwiczenie|2.5.|| | ||
a) Niech <math> | a) Niech <math>T_n(x):=\cos(n\arccos x)</math> dla <math>n=0,1,2,.</math>... | ||
Wykaż, że <math> | Wykaż, że <math>T_0(x)=1</math>, <math>T_1(x)=x</math> oraz | ||
<center><math> | <center><math>T_{n+2}(x) =2x T_{n+1}(x)-T_n (x)</math>,</center> | ||
2x T_{n+1}(x)-T_n (x) | |||
</math></center> | |||
dla <math> | dla <math>n\geq 0</math>.<br> | ||
b) Wykazać, że funkcja <math> | b) Wykazać, że funkcja <math>T_n(x)=\cos(n\arccos x)</math> jest wielomianem | ||
zmiennej <math> | zmiennej <math>x</math>, dla <math>n=0,1,2,3,.</math>... | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Przekształcić | a) Przekształcić | ||
<math> | <math>T_{n+2}</math> oraz <math>T_{n+1}</math>, wykorzystując wzory wyrażające sinus | ||
i cosinus sumy <math> | i cosinus sumy <math>x+y</math>, analogiczne do tych, które zostały wykazane w [[#cwiczenie_2_4|ćwiczeniu 2.4.]], a mianowicie: | ||
<center><math> \ | <center><math>\begin{align} | ||
\cos(x+y)&=\cos x\cos y-\sin x\sin y,\\ | \cos(x+y)&=\cos x\cos y-\sin x\sin y,\\ | ||
\sin(x+y)&=\sin x \cos y+\cos x\sin y. | \sin(x+y)&=\sin x \cos y+\cos x\sin y. | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
| Linia 322: | Linia 292: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Niech <math> | a) Niech <math>y:=\arccos x</math>. Stosując znane | ||
wzory na cosinus i sinus sumy <math> | wzory na cosinus i sinus sumy <math>x+y</math> oraz jedynkę trygonometryczną, | ||
otrzymamy | otrzymamy | ||
<center><math> \ | <center><math>\begin{align} | ||
T_{n+2}(x)&=\cos(n y+2 y)\\ | T_{n+2}(x)&=\cos(n y+2 y)\\ | ||
&=\cos(n y)\cos(2y)-\sin(n y)\sin(2y)\\ | &=\cos(n y)\cos(2y)-\sin(n y)\sin(2y)\\ | ||
&=\cos(ny)(2\cos^2 y-1)-\sin(ny)2\sin y\cos y\\ | &=\cos(ny)(2\cos^2 y-1)-\sin(ny)2\sin y\cos y\\ | ||
&=T_n (x)(2x^2-1)-2 x \sin(n\arccos x) \sin (\arccos x), | &=T_n (x)(2x^2-1)-2 x \sin(n\arccos x) \sin (\arccos x), | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
gdyż <math> | gdyż <math>\cos y=\cos(\arccos x)=x</math> oraz | ||
<math> | <math>\cos ny=\cos(n\arccos x)=T_n(x)</math>. Przekształćmy także | ||
<center><math> \ | <center><math>\begin{align} | ||
T_{n+1}(x)&=\cos(n y+ y)\\ | T_{n+1}(x)&=\cos(n y+ y)\\ | ||
&=\cos(n y)\cos(y)-\sin(n y)\sin(y)\\ | &=\cos(n y)\cos(y)-\sin(n y)\sin(y)\\ | ||
&=T_n (x) x-\sin(n\arccos x) \sin (\arccos x). | &=T_n (x) x-\sin(n\arccos x) \sin (\arccos x). | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
Stąd <math> | Stąd <math>\sin(n\arccos x) \sin (\arccos x)=x T_n (x)-T_{n+1}(x)</math>. | ||
Wobec tego | Wobec tego | ||
<center><math> \ | <center><math>\begin{align} | ||
T_{n+2}(x)&=T_n (x)(2x^2-1)-2 x \sin(n\arccos x) \sin | T_{n+2}(x)&=T_n (x)(2x^2-1)-2 x \sin(n\arccos x) \sin | ||
(\arccos x)\\ | (\arccos x)\\ | ||
&=T_n (x)(2x^2-1)-2 x(x T_n (x)-T_{n+1}(x))\\ | &=T_n (x)(2x^2-1)-2 x(x T_n (x)-T_{n+1}(x))\\ | ||
&=2x T_{n+1}(x)-T_{n}(x). | &=2x T_{n+1}(x)-T_{n}(x). | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
b) Formuła wykazana w punkcie b) pozwala wyznaczyć <math> | b) Formuła wykazana w punkcie b) pozwala wyznaczyć <math>T_{n+2}</math> dla | ||
<math> | <math>n=0,1,2,.</math>... Iloczyn i suma wielomianów jest wielomianem. | ||
Funkcje <math> | Funkcje <math>T_0(x)=1</math> oraz <math>T_1(x)=x</math> są wielomianami zmiennej <math>x</math>, | ||
więc każda kolejna funkcja | więc każda kolejna funkcja | ||
<center><math> \ | <center><math>\begin{align} | ||
T_2(x)&=2xT_1(x)-T_0(x)=2x^2-1, | T_2(x)&=2xT_1(x)-T_0(x)=2x^2-1, T_3(x)&=2xT_2(x)-T_1(x)=4x^3-3x, T_4(x)&=2xT_3(x)-T_2(x)=8x^4-8x^2+1, T_5(x)&=2xT_4(x)-T_3(x)=16x^5-20x^3+5x, ... | ||
T_3(x)&=2xT_2(x)-T_1(x)=4x^3-3x, | \end{align} | ||
T_4(x)&=2xT_3(x)-T_2(x)=8x^4-8x^2+1, | |||
T_5(x)&=2xT_4(x)-T_3(x)=16x^5-20x^3+5x, | |||
\ | |||
</math></center> | </math></center> | ||
jest również wielomianem zmiennej <math> | jest również wielomianem zmiennej <math>x</math>. | ||
</div></div> | </div></div> | ||
<span id="cwiczenie_2_6">{{cwiczenie|2.6.|| | <span id="cwiczenie_2_6">{{cwiczenie|2.6.|| | ||
a) Niech <math> | a) Niech <math>U_n(x):=\cosh(n {\rm arcosh\, } x)</math> dla | ||
<math> | <math>n=0,1,2,.</math>... Wykaż, że <math>U_0(x)=1</math>, <math>U_1(x)=x</math> oraz | ||
<math>U_{n+2}(x) =2xU_{n+1}(x)-U_{n}(x),\quad | |||
</math><br> dla <math>n\geq 0</math>. | |||
2xU_{n+1}(x)-U_{n}(x),\quad | |||
</math | |||
b) Wykazać, że funkcja <math> | b) Wykazać, że funkcja <math>U_n(x)=\cosh(n {\rm arcosh\, } x)</math> jest wielomianem | ||
zmiennej <math> | zmiennej <math>x</math>, dla <math>n=0,1,2,3,.</math>...<br> | ||
c) Wykazać, że dla dowolnej liczby <math> | c) Wykazać, że dla dowolnej liczby <math>n=0,1,2,3,.</math>.. istnieje | ||
wielomian <math> | wielomian <math>W_n</math> taki, że <math>U_n</math> oraz <math>T_n</math> są restrykcjami - | ||
odpowiednio do przedziałów <math> | odpowiednio do przedziałów <math>[1, \infty)</math> oraz <math>[-1, 1]</math> - | ||
wielomianu <math> | wielomianu <math>W_n</math>. | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Warto uprościć | a) Warto uprościć | ||
<math> | <math>U_{n+2}</math> oraz <math>U_{n+1}</math>, wykorzystując wzory wykazane w [[#cwiczenie_2_4|ćwiczeniu 2.4.]]<br> | ||
b) Suma i iloczyn wielomianów jest wielomianem. Wykorzystać | b) Suma i iloczyn wielomianów jest wielomianem. Wykorzystać | ||
formułę z punktu a) zadania.<br> | formułę z punktu a) zadania.<br> | ||
c) Porównać formuły z punktów b) w [[#cwiczenie_2_5|ćwiczeniu 2.5.]] i [[#cwiczenie_2_6|ćwiczeniu 2.6.]] | c) Porównać formuły z punktów b) w [[#cwiczenie_2_5|ćwiczeniu 2.5.]] i [[#cwiczenie_2_6|ćwiczeniu 2.6.]] | ||
Wyznaczyć dziedziny funkcji <math> | Wyznaczyć dziedziny funkcji <math>T_n</math> oraz <math>U_n</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>y:={\rm arcosh\, } x</math>. Postępując podobnie jak | ||
w [[#cwiczenie_2_5|ćwiczeniu 2.5.]] tzn. stosując wykazane w [[#cwiczenie_2_4|ćwiczeniu 2.4.]] wzory na cosinus | w [[#cwiczenie_2_5|ćwiczeniu 2.5.]] tzn. stosując wykazane w [[#cwiczenie_2_4|ćwiczeniu 2.4.]] wzory na cosinus | ||
hiperboliczny i sinus hiperboliczny sumy <math> | hiperboliczny i sinus hiperboliczny sumy <math>x+y</math> oraz jedynkę | ||
hiperboliczną, otrzymamy | hiperboliczną, otrzymamy | ||
<center><math> \ | <center><math>\begin{align} | ||
U_{n+2}(x)&=\cosh(n y+2 y)\\ | U_{n+2}(x)&=\cosh(n y+2 y)\\ | ||
&=\cosh(n y)\cosh(2y)+\sinh(n y)\sinh(2y)\\ | &=\cosh(n y)\cosh(2y)+\sinh(n y)\sinh(2y)\\ | ||
&=\cosh(ny)(2\cosh^2 y-1)+\sinh(ny)2\sinh y\cosh y\\ | &=\cosh(ny)(2\cosh^2 y-1)+\sinh(ny)2\sinh y\cosh y\\ | ||
&=U_n (x)(2x^2-1)+2 x \sinh(n{\rm arcosh\, } x) \sinh ({\rm arcosh\, } x), | &=U_n (x)(2x^2-1)+2 x \sinh(n{\rm arcosh\, } x) \sinh ({\rm arcosh\, } x), | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
gdyż <math> | gdyż <math>\cosh y=\cosh({\rm arcosh\, } x)=x</math> oraz | ||
<math> | <math>\cosh(ny)=\cosh(n{\rm arcosh\, } x)=U_n(x)</math>. Przekształćmy także | ||
<center><math> \ | <center><math>\begin{align} | ||
U_{n+1}(x)&=\cosh(n y+ y)\\ | U_{n+1}(x)&=\cosh(n y+ y)\\ | ||
&=\cosh(n y)\cosh(y)+\sinh(n y)\sinh(y)\\ | &=\cosh(n y)\cosh(y)+\sinh(n y)\sinh(y)\\ | ||
&=U_n (x) x+\sinh(n{\rm arcosh\, } x) \sinh ({\rm arcosh\, } x). | &=U_n (x) x+\sinh(n{\rm arcosh\, } x) \sinh ({\rm arcosh\, } x). | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
Stąd <math> | Stąd <math>\sinh(n{\rm arcosh\, } x) \sinh ({\rm arcosh\, } x)=-x U_n (x)+U_{n+1}(x)</math>. | ||
Wobec tego | Wobec tego | ||
<center><math> \ | <center><math>\begin{align} U_{n+2}(x)&=U_n (x)(2x^2-1)+2 x \sinh(n{\rm arcosh\, } x) \sinh | ||
({\rm arcosh\, } x)\\ | ({\rm arcosh\, } x)\\ | ||
&=U_n (x)(2x^2-1)+2 x(-x U_n (x)+U_{n+1}(x))\\ | &=U_n (x)(2x^2-1)+2 x(-x U_n (x)+U_{n+1}(x))\\ | ||
&=2x U_{n+1}(x)-U_{n}(x). | &=2x U_{n+1}(x)-U_{n}(x). | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
b) Zauważmy, że formuła wykazana w punkcie b) pozwala wyznaczyć | b) Zauważmy, że formuła wykazana w punkcie b) pozwala wyznaczyć | ||
<math> | <math>U_{n+2}</math> dla <math>n=0,1,2,.</math>... Iloczyn i suma wielomianów jest | ||
wielomianem. Ponadto funkcje <math> | wielomianem. Ponadto funkcje <math>U_0(x)=1</math> oraz <math>U_1(x)=x</math> są | ||
wielomianami zmiennej <math> | wielomianami zmiennej <math>x</math>, więc każda kolejna funkcja | ||
<center><math> \ | <center><math>\begin{align} | ||
U_2(x)&=2xU_1(x)-U_0(x)=2x^2-1,\\ | U_2(x)&=2xU_1(x)-U_0(x)=2x^2-1,\\ | ||
U_3(x)&=2xU_2(x)-U_1(x)=4x^3-3x,\\ | U_3(x)&=2xU_2(x)-U_1(x)=4x^3-3x,\\ | ||
U_4(x)&=2xU_3(x)-U_2(x)=8x^4-8x^2+1,\\ | U_4(x)&=2xU_3(x)-U_2(x)=8x^4-8x^2+1,\\ | ||
U_5(x)&=2xU_4(x)-U_3(x)=16x^5-20x^3+5x, \ \ ... | U_5(x)&=2xU_4(x)-U_3(x)=16x^5-20x^3+5x, \ \ ... | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
jest również wielomianem zmiennej <math> | jest również wielomianem zmiennej <math>x</math>.<br> | ||
c) Formuły pozwalające wyznaczyć <math> | c) Formuły pozwalające wyznaczyć <math>T_{n+2}</math> oraz <math>U_{n+2}</math> są | ||
identyczne: | identyczne: | ||
<center><math> \ | <center><math>\begin{align} | ||
T_{n+2}(x)&=2x T_{n+1}(x)-T_{n}, \ \ T_{0}(x)=1, \ \ T_1 (x)=x,\\ | T_{n+2}(x)&=2x T_{n+1}(x)-T_{n}, \ \ T_{0}(x)=1, \ \ T_1 (x)=x,\\ | ||
U_{n+2}(x)&=2x U_{n+1}(x)-U_{n}, \ \ U_{0}(x)=1, \ \ U_1 (x)=x. | U_{n+2}(x)&=2x U_{n+1}(x)-U_{n}, \ \ U_{0}(x)=1, \ \ U_1 (x)=x. | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
Wielomiany <math> | Wielomiany <math>T_n</math> oraz <math>U_n</math> są więc zacieśnieniem -- odpowiednio do przedziałów | ||
<math> | <math>[-1,1]</math> oraz <math>[1,\infty)</math> - tego samego wielomianu <br> <math>W_n</math>, <math>n=0,1,2,.</math>... | ||
Zwróćmy uwagę na fakt, że dziedziną każdej z funkcji | Zwróćmy uwagę na fakt, że dziedziną każdej z funkcji | ||
<math> | <math>T_n(x)=\cos(n\arccos x)</math> jest przedział <math>[-1,1]</math> a dziedziną | ||
funkcji <math> | funkcji <math>U_n(x)=\cosh(n{\rm arcosh\, } x)</math> - przedział <math>[1, +\infty)</math>. | ||
Stąd formalnie równość funkcji <math> | Stąd formalnie równość funkcji <math>T_n (x)=U_n (x)</math> ma sens w części wspólnej obu dziedzin, tj. w punkcie <math>x=1</math>. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 13:11, 22 lip 2024
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a) ,
b) .
Ćwiczenie 2.5.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
Ćwiczenie 2.6.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
c) Wykazać, że dla dowolnej liczby .. istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .