Układy elektroniczne i technika pomiarowa/Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| (Nie pokazano 3 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
{| border="0" | {| border="0" cellpadd<math>Insert formula here</math>ing="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
| Linia 95: | Linia 95: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Właściwości filtru dolnoprzepustowego''' | ||
Jeżeli sygnał sterujący <math>u_1</math> nie zawiera składowej stałej, a jego pulsacja spełnia warunek <math>\omega>>\omega_g</math> to filtr dolnoprzepustowy działa jak układ całkujący. | |||
Jeżeli sygnał sterujący <math>u_1</math> oprócz składowej przemiennej zawiera składową stałą, | |||
<math>u_1(t)\frac{1}{\tau}\int^t_0 u_p(\delta)d\delta+U_0</math> | |||
Pierwszy składnik sumy reprezentuje tętnienia, a drugi składową stałą. | |||
Jeżeli stała czasowa jest bardzo duża składnik reprezentujący tętnienia można pominąć i napięcie wyjściowe jest równe w tym wypadku składowej stałej. | |||
Jedną z wielkości charakteryzujących filtr dolnoprzepustowy jest czas narastania <math>t_r</math>. Podaje on, w jakim czasie napięcie wyjściowe filtru wzrośnie od 10% do 90% wartości ustalonej po zadaniu na wejściu układu skoku jednostkowego. | |||
<math>t_r=t_{90%}-t_{10%}=\tau(ln0,9-ln0,1)=\tauln9\approx2,2\tau</math> | |||
Przy częstotliwości granicznej czas <math>t_r</math> jest równy w przybliżeniu: | |||
<math>t_r\approx\frac{1}{3f_g}</math> | |||
Związek ten obowiązuje także dla filtrów dolnoprzepustowych wyższych rzędów. Jeżeli czasy narastania poszczególnych filtrów składowych są różne to wypadkowy czas narastania jest średnią geometryczną poszczególnych czasów. | |||
<math>t_r\approx\sqrt{\sum_{i=0}^n}t_r_i^2</math> | |||
Częstotliwość graniczna takiego filtru jest równa | |||
<math>f_g\approx \frac{1}{\sum{_{i=1}^n\frac{1}{f_{gi}^2}}}</math> | |||
Kiedy połączymy kaskadowo n jednakowych filtrów | |||
<math>f_g\frac{f_{gi}}{n}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 101: | Linia 130: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Filtr górnoprzepustowy''' | ||
Opis w dziedzinie częstotliwości | |||
Transmitancja widmowa układu ma postać: | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{j\omega T}{1+j\omega T}</math> | |||
Moduł transmitancji widmowej i faza sygnału wyjściowego względem wejściowego po znormalizowaniu pulsacji przebiegu względem pulsacji granicznej <math>\omega d</math> jest równy: | |||
<math>|T(jx)|=\frac{1}{\sqrt{1+\frac{1}{x^2\omega^2_dT^2}}}=\frac{1}{\sqrt{1+\frac{1}{x^2}}}</math> | |||
<math>\varphi=arctg\frac{1}{x\omega_dT}=arctg\frac{1}{x}</math> | |||
gdzie | |||
<math>x=\frac{\omega}{\omega_d} (0<x<\infty)</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 107: | Linia 154: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Charakterystyki częstotliwościowe przedstawiono na rysunku. | ||
Pulsacja i częstotliwość graniczna są równe: | |||
<math>\omega_d=\frac{1}{T}</math> | |||
<math>f_d=frac{1}{2\piT}</math> | |||
Przesunięcie fazowe przy tej częstotliwości jest równe <math>frac{\pi}{4}</math> . Szybkość wznoszenia się charakterystyki 20 dB / dekadę. | |||
|} | |} | ||
---- | ---- | ||
| Linia 113: | Linia 168: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Opis w dziedzinie czasu''' | ||
Na slajdzie przedstawiono odpowiedź układów RC i RL przy załączeniu i wyłączeniu napięcia wejściowego. | |||
W przypadku złączenia napięcie wyjściowe zmienia się wykładniczo zgodnie | |||
z zależnością: | |||
<math>u_2(t)U_Me^{-\frac{t}{\tau}}</math>a przy wyłączeniu | |||
<math>u_2(t)U_Me^{-\frac{t}{\tau}}</math> | |||
Podobnie jak w układzie filtru dolnoprzepustowego wartość ustalona u2 = 0 V jest osiągana asymptotycznie. Miarą czasu dojścia do stanu ustalonego jest stała czasowa <math>\tau</math>. Często zakładamy, że po czasie <math>5\tau</math> jest już stan ustalony. W tym wypadku różnica pomiędzy wartością ustaloną i rzeczywista stanowi mniej niż 1% wartości ustalonej. | |||
|} | |} | ||
---- | ---- | ||
| Linia 119: | Linia 186: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Właściwości filtru górnoprzepustowego''' | ||
Jeżeli na wejście jest zadany sygnał prostokątny o pulsacji <math>\omega >>\omega_d</math> to po czasie równym połowie okresu na wyjściu układu filtru nie będzie wartości ustalonej napięcia i przebieg będzie podobny do przebiegu sygnału wejściowego, ale nie będzie zawierał składowej stałej. Dlatego filtr górnoprzepustowy, a szczególnie układ RC jest stosowany jako układ sprzęgający (np. w sprzężeniach międzystopniowych wzmacniaczy mcz.). Jeżeli sygnał wejściowy ma pulsację <math>\omega<<\omega_d</math> to można przyjąć, że <math>u_2 << u_1</math>. W tym wypadku układ ma właściwości różniczkujące. | |||
<math>u_2=\tau\frac{du_1}{dt}</math> | |||
Częstotliwość graniczna filtru górnoprzepustowego n-tego rzędu jest równa: | |||
<math>f_d=\sqrt{\sum_{i=1}^n}f^2_{di}</math> | |||
lub dla kaskadowego połączenia n identycznych filtrów I rzędu | |||
<math>f_d=f_{di}\sqrt{n}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 125: | Linia 205: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Filtr pasmowoprzepustowy RC''' | ||
Łącząc kaskadowo filtr górnoprzepustowy i dolnoprzepustowy otrzymuje się filtr pasmowoprzepustowy. Przykład takiego filtru przedstawiono na rysunku. Transmitancja widmowa takiego układu jest równa: | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{j\omega T}{1+3j\omega T-\omega^2 T^2}</math> | |||
gdzie | |||
<math>T=\tau=RC</math> | |||
Moduł transmitancji widmowej i faza sygnału wyjściowego względem wejściowego, po znormalizowaniu pulsacji przebiegu względem pulsacji rezonansowej <math>\omega_0</math>, jest równy | |||
<math>|T(jx)|=\frac{1}{\sqrt{9+\Bigg(\frac{1}{x\omega_0T}-x\omega_0T\Bigg)^2}}=\frac{1}{\sqrt{9+( | |||
frac{1}{x}-x)^2}}</math> | |||
<math>\varphi=arctg\frac{1-x^2\omega_0^2T^2}{3x\omega_0T}=arctg\frac{1-x^2}{3x}</math> | |||
gdzie | |||
<math>x=\frac{\omega}{\omega_0}</math> | |||
Pulsacja i częstotliwość rezonansowa są równe: | |||
<math>\omega_0=\frac{1}{RC}</math> | |||
<math>f_0=\frac{1}{2\pi RC}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 131: | Linia 238: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd13.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Charakterystyki amplitudowa i fazowa filtru pasmowoprzepustowego są przedstawione na slajdzie. | ||
Dla częstotliwości rezonansowej moduł transmitancji jest największy i równy <math>\frac{1}{3}</math> , | |||
a przesunięcie fazowe jest równe zeru. | |||
|} | |} | ||
---- | ---- | ||
| Linia 137: | Linia 247: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Filtr pasmowozaporowy z mostkiem Wiena –Robinsona. W ogólnym przypadku transmitancja widmowa tego układu jest równa: | ||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{\eta (1-\omega^2T^2)+j\omegaT(3\eta -1)}{1+3j\omega T-\omega^2T^2}</math> | |||
gdzie | |||
<math>T=\tau=RC</math> | |||
<math>\eta=\frac{R_2}{R_1+R_2}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 143: | Linia 263: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przy założeniu, że współczynnik podziału dzielnika napięcia jest równy <math>\eta=\frac{1}{3}</math> | ||
moduł transmitancji widmowej i faza sygnału wyjściowego względem wejściowego, po znormalizowaniu pulsacji przebiegu względem pulsacji rezonansowej <math>\omega_0</math>, jest równy: | |||
<math>|T(jx)|=\frac{|1-x^2\omega^2_0T^2|}{3\sqrt{9x^2\omega^2_0T^2+(1-x^2\omega^2_0T^2)^2}}=\frac{|1-x^2|}{3\sqrt{9x^2+(1-x^2)^2}}</math> | |||
<math>\varphi=arctg\frac{3x\omega_0T}{x^2\omega^2_0T^2-1}=arctg\frac{3x}{x^2-1}, x\ne 1</math> | |||
gdzie | |||
<math>x=\frac{\omega}{\omega_0} (0<x<\infty)</math> | |||
Pulsacja i częstotliwość rezonansowa są równe: | |||
<math>\omega_0=\frac{1}{RC}</math> | |||
<math>f_0\frac{1}{2\pi RC}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 149: | Linia 285: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd16.png|thumb|500px]] | ||
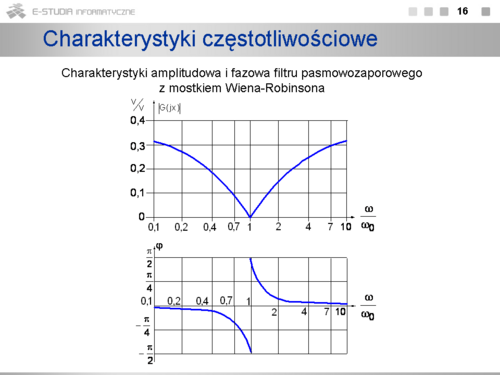
|valign="top"| | |valign="top"|Charakterystyki amplitudowa i fazowa filtru pasmowozaporowego z mostkiem Wiena-Robinsona są przedstawione na slajdzie. Dla częstotliwości rezonansowej moduł amplitudy jest najmniejszy i równy zeru, a faza jest nie określona | ||
|} | |} | ||
---- | ---- | ||
| Linia 155: | Linia 291: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd17.png|thumb|500px]] | ||
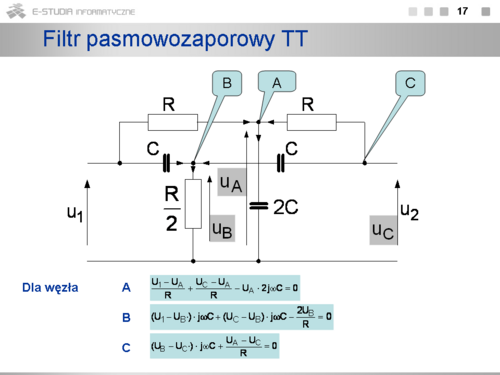
|valign="top"| | |valign="top"|Filtr pasmowozaporowy w układzie TT. | ||
Charakterystyki częstotliwościowe można wyznaczyć stosując prawo Kirchhoffa dla węzłów A, B i C przy nieobciążonym układzie. | |||
Dla węzła A jest | |||
<math>\frac{U_1-U_A}{R}+\frac{U_C-U_A}{R}-U_A\cdot 2j\omegaC=0</math> | |||
Dla węzła B jest | |||
<math>(U_1-U_B)\cdot j\omegaC+(U_C-U_B)\cdot j\omega C-\frac{2U_B}{R}=0</math> | |||
Dla węzła C jest | |||
<math>(U_B-U_C)\cdot j\omega C+\frac{U_A-U_C}{R}=0</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 161: | Linia 312: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd18.png|thumb|500px]] | ||
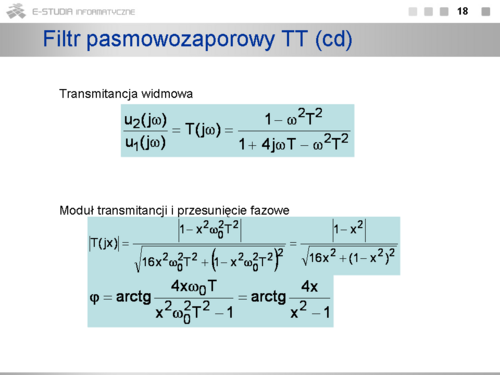
|valign="top"| | |valign="top"|Eliminując z tego układu równań napięcia <math>U_A</math> i <math>U_B</math> oraz przyjmując, że <math>U_2=U_C</math> transmitancja widmowa układu jest opisana zależnością: | ||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{1-\omega^2T^2}{1+4j\omega T-\omega^2T^2}</math> | |||
Moduł transmitancji widmowej i faza sygnału wyjściowego względem wejściowego, po znormalizowaniu pulsacji przebiegu względem pulsacji rezonansowej <math>\omega_0,</math> jest równy: | |||
<math>|T(jx)|=\frac{|1-x^2\omega^2_0T^2|}{\sqrt{16x@\omega^2_0T^2+(1-x^2\omega^2_0T^2)^2}}=\frac{|1-x^2|}{\sqrt{16x^2+(1-x^2)^2}}</math> | |||
<math>\varphi=arctg\frac{4x\omega_0T}{x^2\omega^2_0T^2-1}=arctg\frac{4x}{x^2-1}, x/ne 1</math> | |||
gdzie | |||
<math>x=\frac{\omega}{\omega_0} (0<x<\infty)</math> | |||
Pulsacja i częstotliwość rezonansowa są równe: | |||
<math>\omega_0=\frac{1}{RC}</math> | |||
<math>f_0=\frac{1}{2\pi RC}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 167: | Linia 339: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd19.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd19.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Charakterystyki amplitudowa i fazowa filtru pasmowozaporowego z układem TT są podobne do charakterystyk filtru z mostkiem Wiena-Robinsona. Dla częstotliwości rezonansowej moduł amplitudy jest najmniejszy i równy zeru, a faza jest nieokreślona. | ||
|} | |} | ||
---- | ---- | ||
| Linia 173: | Linia 345: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd20.png|thumb|500px]] | ||
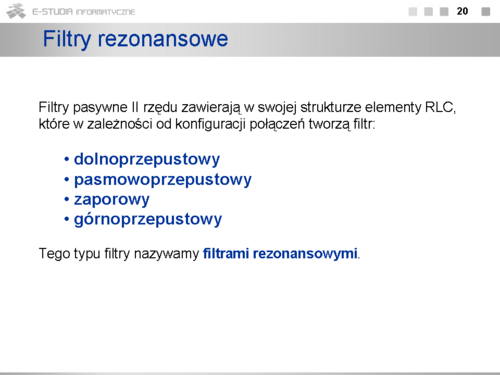
|valign="top"| | |valign="top"|Filtry pasywne II rzędu zawierają w swojej strukturze elementy RLC, które w zależności od konfiguracji połączeń tworzą filtr: | ||
• dolnoprzepustowy | |||
• pasmowoprzepustowy | |||
• zaporowy | |||
• górnoprzepustowy | |||
Tego typu filtry nazywamy filtrami rezonansowymi. | |||
|} | |} | ||
---- | ---- | ||
| Linia 179: | Linia 362: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd21.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Odpowiednie schematy ideowe filtru dolnoprzepustowego i filtru górnoprzepustowego przedstawiono na slajdzie 21. Transmitancje widmowe tych filtrów są opisane zależnościami: | ||
- filtr dolnoprzepustowy | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{1}{1+j\omega RC-\omega^2 LC}</math> | |||
- filtr górnoprzepustowy | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)=\frac{-\omega^2 LC}{1+j\omega RC-\omega^2 LC}</math> | |||
Ponieważ w mianownikach obu wyrażeń operator <math>j\omega</math> występuje w drugiej potędze, <math>(j\omega\cdot j \omega=-\omega^2)</math> mówimy, że filtry są II rzędu. | |||
Znormalizowany moduł transmitancji widmowej są odpowiednio równe | |||
- filtr dolnoprzepustowy | |||
<math>|T(jx)|=\frac{1}{\sqrt {x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{1}{\sqrt{x^2+(1-x^2)^2}}</math> | |||
- filtr górnoprzepustowy | |||
<math>|T(jx)|=\frac{x^2\omega_d^2 LC}{\sqrt { x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{x^2}{\sqrt{x^2+(1-x^2)^2}}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 185: | Linia 389: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd22.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Odpowiednie schematy ideowe filtru zaporowego i filtru pasmowoprzepustowego przedstawiono na slajdzie 22. W tym wypadku znormalizowany moduł transmitancji widmowej i przesunięcie fazowe są odpowiednio równe: | ||
- filtr pasmowoprzepustowy | |||
<math>|T(jx)|=\frac{x\omega_0 RC}{\sqrt { x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{x}{\sqrt{x^2+(1-x^2)^2}}</math> | |||
- filtr pasmowozaporowy | |||
<math>|T(jx)|=\frac{|1-x^2\omega_0^2LC|}{\sqrt { x^2\omega^2_g R^2C^2+(1-x^2\omega_g^2 LC)^2}}=\frac{|1-x^2|}{\sqrt{x^2+(1-x^2)^2}}</math> | |||
Charakterystycznym parametrem filtrów pasmowych i rezonansowych jest pasmo przenoszenia B i dobroć filtru Q, definiowana jako: | |||
<math>Q=\frac{f_0}{B}</math> , gdzie f0 częstotliwość rezonansowa lub częstotliwość środkowa filtru. | |||
Pasmo przenoszenia wyznacza się przyjmując, że na krańcach pasma, dla częstotliwości dolnej i częstotliwości górnej, moduł transmitancji widmowej różni się od wartości jaką ma przy częstotliwości środkowej lub rezonansowej o ±3 dB. | |||
|} | |} | ||
---- | ---- | ||
| Linia 191: | Linia 408: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd23.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Filtry aktywne''' | ||
W zakresie małych częstotliwości realizacja filtrów rezonansowych stwarza wiele trudności. Ponieważ wartości indukcyjności dławików w obwodach filtrów są duże, zatem ich wykonanie jest trudne, a to w efekcie prowadzi do tego, że ich właściwości elektryczne nie są zadawalające. Dlatego, aby uniknąć tej sytuacji do typowych układów pasywnych z elementami RC dołącza się dodatkowy element aktywny. Takie układy nazywamy filtrami aktywnymi. Tego typu układy, w których rolę elementu aktywnego obecnie najczęściej pełni wzmacniacz operacyjny, są produkowane także w postaci gotowych układów scalonych. Filtry aktywne są filtrami sygnałowymi. Celem ich stosowania jest wydzielenie z sygnału roboczego sygnału użytecznego przy jednoczesnym stłumieniu zakłóceń. Podobnie jak w układach pasywnych filtr aktywny jest opisany transmitancją widmowa, z której można wyznaczyć charakterystyki częstotliwościowe układu oraz odpowiednie pulsacje lub częstotliwości (graniczne: dolną i górną, środkową lub rezonansową) oraz dla filtrów pasmowych pasmo częstotliwości przepuszczanych lub tłumionych i dobroć filtru. | |||
Cechy filtrów aktywnych | |||
• możliwość wzmacniania sygnałów użytecznych | |||
• możliwość realizacji filtrów selektywnych o częstotliwości środkowej (rezonansowej) rzędu 0,01 Hz i bardzo dużych dobrociach Q | |||
• brak wpływu obciążenia na charakterystyki filtru | |||
• łatwe i niezależne strojenie parametrów filtru (częstotliwość, wzmocnienie, dobroć) | |||
• możliwość budowy filtrów uniwersalnych. | |||
|} | |} | ||
---- | ---- | ||
| Linia 197: | Linia 428: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd24.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd24.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Filtry dolnoprzepustowe i górnoprzepustowe I rzędu''' | ||
Schemat filtrów dolnoprzepustowych przedstawiono na slajdzie. Transmitancja widmowa układu powtarzającego ma postać | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)\frac{R_1+R_2}{R_2}\cdot \frac{1}{1+j\omega T}</math> | |||
gdzie | |||
<math>T=\tau=RC</math> | |||
a układu odwracającego | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)\frac{R_2}{R_1}\cdot \frac{1}{1+j\omega T}</math> | |||
gdzie | |||
<math>T=\tau=R_2C</math> | |||
Pulsacja i częstotliwość graniczna są równe | |||
<math>\omega_g=\frac{1}{T}</math> | |||
<math>f_g=\frac{1}{2\pi T}</math> | |||
Charakterystyki częstotliwościowe są takie jak dla filtru pasywnego, przy czym charakterystyka amplitudowa jest przesunięta w pionie o wartość odpowiadającą ustawionemu w układzie wzmocnieniu (w skali dB). | |||
|} | |} | ||
---- | ---- | ||
| Linia 203: | Linia 460: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd25.png|thumb|500px]] | ||
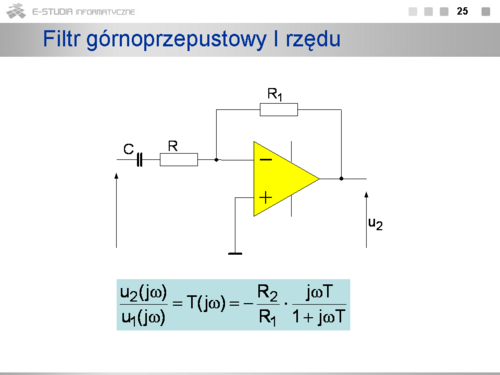
|valign="top"| | |valign="top"|'''Filtr górnoprzepustowy''' | ||
Transmitancja widmowa jest opisana zależnością: | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)\frac{R_2}{R_1}\cdot \frac{j\omega T}{1+j\omega T}</math> | |||
gdzie | |||
<math>T=\tau=R_1C_1</math> | |||
Jak wynika z zależności 5.62 zmiana rezystora R2 powoduje zmianę wzmocnienia układu przy czym zmiana ta nie ma wpływu na częstotliwość graniczną filtru, która zależy wyłącznie od wartości elementów R1 i C1. | |||
Odpowiednio pulsacja i częstotliwość graniczna dolna opisane są wzorami: | |||
<math>\omega_g=\frac{1}{T}</math> | |||
<math>f_g=\frac{1}{2\pi T}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 209: | Linia 482: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd26.png|thumb|500px]] | ||
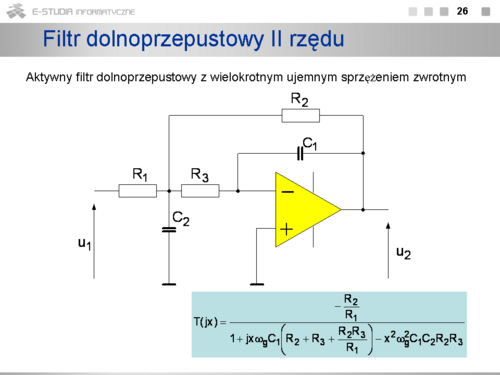
|valign="top"| | |valign="top"|'''Filtry dolnoprzepustowy i górnoprzepustowy II rzędu''' | ||
Aktywny filtr dolnoprzepustowy z wielokrotnym ujemnym sprzężeniem zwrotnym. Schemat ideowy filtru przedstawiono na rysunku. Znormalizowana względem ωg transmitancja widmowa tego układu opisana jest zależnością: | |||
<math>T(jx)=\frac{-\frac{R_2}{R_1}}{1+jx\omega_g C_1(R_2+R_3+\frac{R_2R_3}{R_1})-x^2\omega^2_gC_1C_2R_2R_3}</math> | |||
gdzie | |||
<math>x=\frac{\omega}{\omega_g} (0<x<\infty)</math> | |||
Podana transmitancja widmowa układu jest prawdziwa, jeżeli założymy, że wzmacniacz operacyjny jest idealny. Warunek ten może być spełniony kiedy zastosujemy do realizacji układu szybki wzmacniacz operacyjny. | |||
Przy projektowaniu najczęściej zakłada się, że znane są wartości pojemności kondensatorów, a oblicza się rezystancje. | |||
W przypadku ogólnym transmitancję widmową dla dowolnego filtru dolnoprzepustowego II rzędu można zapisać w postaci: | |||
<math>T(jx)=\frac{k_u_0}{1+jxa_1-x^2b_1}</math> | |||
Współczynniki <math>k_u_0</math> ustala wzmocnienie układu dla składowej stałej i jest przyjmowany dowolnie w zależności od potrzeb. Współczynniki <math>a_1</math> oraz <math>b_1</math> są dodatnie i mają określone stałe wartości, które zostały stabelaryzowane w zależności od rodzaju realizowanego filtru. Do najpopularniejszych należą filtry: | |||
• z tłumieniem krytycznym | |||
• Bessela | |||
• Butterwortha | |||
• Czejbyszewa | |||
W zależności od rodzaju filtru odpowiednio wybrane wartości współczynników a1, b1 umożliwiają realizację odpowiedniego kształtu charakterystyki amplitudowej filtru. | |||
Np. realizując filtr z tłumieniem krytycznym należy przyjąć następujące wartości współczynników: | |||
<math>a_1 = 1,2872, b_1 = 0,4142</math> | |||
Omawiany tutaj filtr dolnoprzepustowy z wielokrotnym ujemnym sprzężeniem zwrotnym dla składowej stałej odwraca fazę sygnału (ku0 < 0), a zatem można wnioskować, że podobnie dzieje się dla sygnałów w zakresie małych częstotliwości. | |||
Obliczone rezystancje <math>R_1, R_2, R_3</math> przy zadanych wartościach pojemności kondensatorów są rzeczywiste (dodatnie), gdy jest spełniony warunek | |||
<math>\frac{C_2}{C_1}>\frac{4b_1(1-k_u_0)}{a_1^2}</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 215: | Linia 521: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd27.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd27.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Aktywny filtr dolnoprzepustowy można r\'{o}wnież zrealizować obejmując | ||
wzmacniacz operacyjny, w kt\'{o}rym dokładnie ustalono wzmocnienie | |||
napięciowe za pomocą ujemnego sprzężenia zwrotnego, pętlą dodatniego | |||
sprzężenia zwrotnego. \newline | |||
W układzie jak na rysunku sprzężenie dodatnie jest realizowane przez | |||
elementy <math>R$_{1}$, R$_{2}$, C$_{1}$, C$_{2}$</math>, a sprzężenie ujemne przez | |||
elementy <math>(k$_{u0}$ -- 1)R$_{3}$ oraz R$_{3}$</math>. | |||
|} | |} | ||
---- | ---- | ||
Aktualna wersja na dzień 14:10, 26 paź 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |