MO Moduł 10: Różnice pomiędzy wersjami

← poprzednia edycja

WizualnieWikikod

Aktualna wersja na dzień 10:34, 5 wrz 2023

Widać, że jednoczesna maksymalizacja obu kryteriów na zbiorze dopuszczalnym nie jest możliwa. Po dojściu do „północno-wschodniej” granicy zbioru powiększenie jednego kryterium, powoduje zmniejszenie drugiego kryterium.

Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący

P = {(q_{1}, q_{2}) \in [60, 140] \times [14, 46] | q_{2} = 70 - \frac{2}{5} q_{1}}

,

to podejście utylitarianistyczne oparte na maksymalizacji sumy
$(q_{1}, q_{2}) \mapsto u (q_{1}, q_{2}) = q_{1} + q_{2}$
jako rozwiązanie da $(q_{1}^{B}, q_{2}^{B}) = (140, 14)$ oraz decyzję $(x_{1}^{B}, x_{2}^{B}) = (14, 0)$ – tylko pracować. (Dobrze jest wykonać stosowny rysunek.)

Przypisanie wag poszczególnym kryteriom oznacza posłużenie się funkcją

(q_{1}, q_{2}) \mapsto u_{β} (q_{1}, q_{2}) = q_{1} + β q_{2}

,

gdzie współczynnik $β$ można interpretować jako cenę jednostki zadowolenia. Zauważmy, że dla $β = \frac{5}{2}$ , każdy punkt ze zbioru Pareto daje tą samą wartość funkcji $u_{β}$ .
Dla $β < \frac{5}{2}$ rozwiązaniem będzie $(q_{1}^{β}, q_{2}^{β}) = (140, 14)$ i $(x_{1}^{β}, x_{2}^{β}) = (14, 0)$ – punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów.
Dla $β > \frac{5}{2}$ jako rozwiązanie otrzymamy $(q_{1}^{β}, q_{2}^{β}) = (60, 46)$ oraz $(x_{1}^{β}, x_{2}^{β}) = (6, 8)$ – punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie.
(Dobrze jest wykonać stosowne rysunki.)

Podejście oparte na zasadzie sprawiedliwości jako rozwiązanie da

(q_{1}^{R}, q_{2}^{R}) = (60, 46)

oraz jako wybrany wariant

(x_{1}^{R}, x_{2}^{R}) = (6, 8)

.

Nie zawsze prosta o nachyleniu 45° przecina zbiór Pareto !

Punkt idealny dla pana X to

(q_{1}^{U}, q_{2}^{U}) = (140, 46)

, punkt nadiru

(q_{1}^{N}, q_{2}^{N}) = (50, 5)

. Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt

(q_{1}, q_{2}) = (128.9655, 18.4138)

czyli wybranymi wariantami powinna być para

(x_{1}, x_{2}) = (12.8966, 1.1034)

. Oczywiście pan X zaokragli ten wynik i przy takim sposobie wyboru decyzji bedzie pracował przez 13 godzin a tylko godzinę czytał, co da mu 130 zł i 18 jednostek zadowolenia.

Dla tej samej metryki, punktem najdalej położonym w stosunku do nadiru jest punkt $(q_{1}, q_{2}) = (140, 14)$ określony przez warianty $(x_{1}, x_{2}) = (14, 0)$ (tylko pracować). (Dobrze jest wykonać stosowne rysunki.)

@@ Linia 121: / Linia 121: @@
 {| border="0" cellpadding="4" width="125%"
 |width="500px" valign="top"|[[Grafika:MO_M10_Slajd21.png|thumb|500px]]
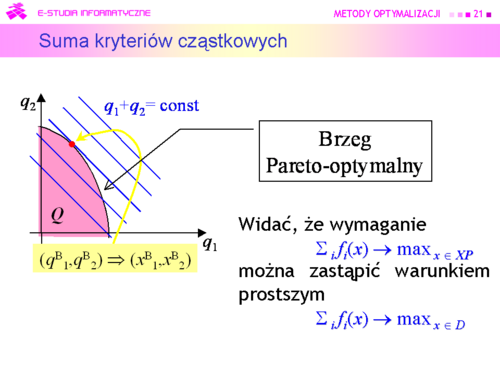
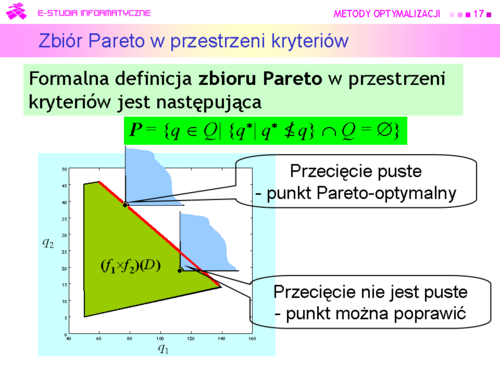
-|valign="top"|Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący
+|valign="top"|Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący<br><math>\boldsymbol{P} = \{(q_1,q_2) \in [60,140] \times [14,46] |\, q_2 =70 - {2 \over 5}q_1 \}</math>,
- ,
+to '''podejście utylitarianistyczne''' oparte na maksymalizacji sumy<br><math>(q_1,q_2) \mapsto u(q_1,q_2) = q_1 + q_2</math><br>
-to podejście utylitarianistyczne oparte na maksymalizacji sumy
+jako rozwiązanie da <math>(q_1^{\mathrm B},q_2^{\mathrm B})= (140,14)</math> oraz decyzję <math>(x_1^{\mathrm B},x_2^{\mathrm B})=(14,0)</math> – '''tylko pracować'''. (Dobrze jest wykonać stosowny rysunek.)
-jako rozwiązanie da   oraz decyzję   – tylko pracować. (Dobrze jest wykonać stosowny rysunek.)
 |}
@@ Linia 132: / Linia 130: @@
 {| border="0" cellpadding="4" width="125%"
 |width="500px" valign="top"|[[Grafika:MO_M10_Slajd22.png|thumb|500px]]
-|valign="top"|Przypisanie wag poszczególnym kryteriom oznacza posłużenie się funkcją
+|valign="top"|Przypisanie wag poszczególnym kryteriom oznacza posłużenie się funkcją <br><math>(q_1,q_2)\mapsto u_\beta(q_1,q_2)= q_1 + \beta q_2</math>,
- ,
+gdzie współczynnik <math>\beta</math> można interpretować jako '''cenę''' jednostki zadowolenia.
-gdzie współczynnik b można interpretować jako cenę jednostki zadowolenia.
+Zauważmy, że dla <math>\beta={5 \over 2}</math>, '''każdy punkt ze zbioru Pareto daje tą samą wartość funkcji'''  <math>\boldsymbol{u_\beta}</math>.<br> Dla <math>\beta < {5 \over 2}</math> rozwiązaniem będzie <math>(q_1^{\beta},q_2^{\beta})= (140,14)</math> i <math>(x_1^{\beta},x_2^{\beta})=(14,0)</math> – punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów.<br> Dla <math>\beta > {5\over2}</math> jako rozwiązanie otrzymamy <math>(q_1^{\beta},q_2^{\beta})= (60,46)</math> oraz <math>(x_1^{\beta},x_2^{\beta})=(6,8)</math> – punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie.<br>(Dobrze jest wykonać stosowne rysunki.)
-Zauważmy, że dla b = 5/2, każdy punkt ze zbioru Pareto daje tą samą wartość funkcji ub, dla b < 5/2 rozwiązaniem będzie   i   –punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów. Dla b > 5/2 jako rozwiązanie otrzymamy   oraz   – punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie. (Dobrze jest wykonać stosowne rysunki.)
 |}
@@ Linia 148: / Linia 145: @@
 {| border="0" cellpadding="4" width="125%"
 |width="500px" valign="top"|[[Grafika:MO_M10_Slajd24.png|thumb|500px]]
-|valign="top"|Podejście oparte na zasadzie sprawiedliwości jako rozwiązanie da
+|valign="top"|Podejście oparte na '''zasadzie sprawiedliwości''' jako rozwiązanie da <math>(q_1^{\mathrm R},q_2^{\mathrm R}) = (60,46)</math> oraz jako wybrany wariant <math>(x_1^{\mathrm R},x_2^{\mathrm R}) = (6,8)</math>.
-  oraz jako wybrany wariant  .
 Nie zawsze prosta o nachyleniu 45° przecina zbiór Pareto !
@@ Linia 169: / Linia 165: @@
 {| border="0" cellpadding="4" width="125%"
 |width="500px" valign="top"|[[Grafika:MO_M10_Slajd27.png|thumb|500px]]
-|valign="top"|Punkt idealny dla pana X to  , punkt nadiru  . Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt   czyli wybranymi wariantami powinna być para  .
+|valign="top"|'''Punkt idealny''' dla pana X to <math>(q_1^{\mathrm U},q_2^{\mathrm U})=(140,46)</math>, '''punkt nadiru''' <math>(q_1^{\mathrm N},q_2^{\mathrm N})=(50,5)</math>. Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt <math>(q_1,q_2)=(128.9655,\,18.4138)</math> czyli wybranymi wariantami powinna być para <math>(x_1,x_2)=(12.8966,\,1.1034)</math>. Oczywiście pan X zaokragli ten wynik i przy takim sposobie wyboru decyzji bedzie pracował przez 13 godzin a tylko godzinę czytał, co da mu 130 zł i 18 jednostek zadowolenia.
-Dla tej samej metryki, punktem najdalej położonym w stosunku do nadiru jest punkt   określony przez warianty   (tylko pracować).
+Dla tej samej metryki, punktem najdalej położonym w stosunku do nadiru jest punkt  <math>(q_1,q_2)=(140,14)</math>  określony przez warianty <math>(x_1,x_2)=(14,0)</math>  (tylko pracować).
 (Dobrze jest wykonać stosowne rysunki.)
 |}
 ----

MO Moduł 10: Różnice pomiędzy wersjami

Aktualna wersja na dzień 10:34, 5 wrz 2023

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia